벡터가 뭐예요?
이번 장에서는 ML의 기초라고 할 수 있는 벡터에 대하여 학습을 진행했다.
경영학을 전공하여 대학에서 선형대수학을 배울 기회가 없었지만,
이번 시간을 통해서 선형대수학의 기초인 벡터에 대하여 자세히 공부할 수 있어 정말 좋았다.
00. 공부 내용
- 벡터의 정의에 대하여 공부
- 벡타의 연산(덧셈, 뺄셈, 성분곱)에 대하여 공부
- 벡터의 노름에 대하여 공부
- 두 벡터의 거리, 각도를 계산하는 방법에 대하여 공부
- 벡터의 내적에 대하여 공부
01. 벡터의 정의
- 벡터는 숫자를 원소로 가지는 리스트 또는 배열을 의미한다.
- 백터는 열벡터와 행벡터로 나뉘어진다.
- 벡터는 공간에서의 한 점을 의미한다.
- 벡터는 원점으로부터 상대적 위치를 표현한다.
- 즉, [1, 2, 3] 이라는 행 벡터가 존재할때, 이 벡터는 3차원을 가지는 하나의 점을 의미하며, 점의 위치는 원점으로 부터 x = 1, y = 2, z = 3 만큼 떨어진 곳에 위치하게 된다.
02. 벡터의 연산
- 벡터에 스칼라 곱을 하며, 스칼라 곱의 범위에 따라서 벡터의 위치가 바뀌게 된다.
- 예를 들어 음수를 곱하면 벡터의 방향이 반대로 바뀌며, 소수를 곱하면 벡터의 크기가 작아지며, 벡터에 1보다 큰 양수를 곱하면 그 값이 커진다.
- 두 개의 벡터의 모양이 같다면, 덧셈과 뺄셈이 가능하고, 각 성분끼리 곱하는 element-wise product(Hadamard product) 계산이 가능하다.
- 여기서 벡터의 덧셈과 뺄셈은 다른 벡터로 부터의 상대적 위치 이동으로 생각할 수 있다. (왜? 하나의 벡터는 어떻게 보면 원점으로 부터의 상대적 위치 이동이라고 생각할 수 있기 때문에)
- 벡터의 성분곱은 두 벡터의 차원 중 서로 같은 방향을 바라보는 차원의 값을 크게 만드는 과정이라고 생각할 수 있다.(두 벡터의 값이 양수 or 음수면 양수의 방향으로, 두 벡터의 값이 음수와 양수면 음수의 방향으로)
03. 벡터의 노름
- 벡터의 norm은 원점에서부터의 거리를 의미한다.
- 벡터의 norm은 크게 L1 norm, L2 norm 으로 나뉘어 진다.
- L1 norm은 다음과 같은 식으로 계산할 수 있으며, 각 성분의 변화량의 절대값을 모두 더하는 방식이며, 이는 맨하튼 거리로도 볼 수 있다.
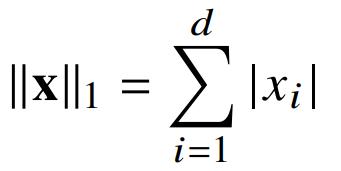
- L2 norm은 다음과 같은 식으로 계산할 수 있으며, 각 성분의 변화량의 제곱값을 모두 더하며 루트를 쒸우는 방식이며, 이는 피타고라스 정리를 이용한 유클리드 거리로도 볼 수 있다.
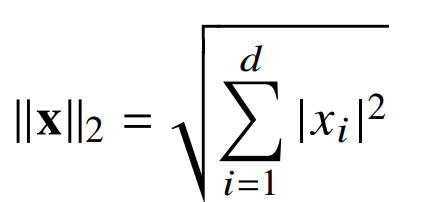
- 이렇듯 L1과 L2 norm은 각각 거리를 계산하는 정의가 다르기 때문에 기하학적 성질, 즉 원을 바라보는 관점이 달라지게 된다.
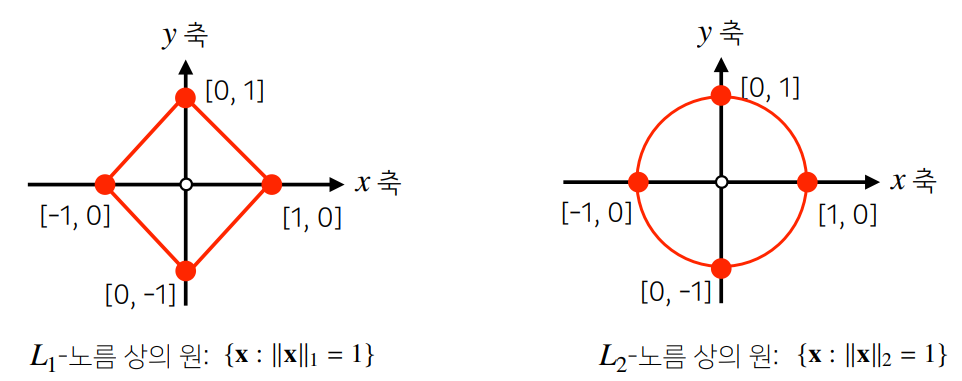
- L1 Norm의 경우 각 좌표의 방향을 따라가는 방식(맨하든 거리)이기 때문에, 변수의 영향력을 0으로 만들 수 있어 조금 더 Robust 즉 강건한 학습에 적합하며 Lasso 회귀에 사용되어 변수 선택의 기능으로써도 활용할 수 있다.
- L2 Norm의 경우 각 좌표를 대각선으로 가로지르는 방식(유클리디안)이기 때문에, 모든 변수를 어떻게든 활용하며(변수의 영향력을 0으로 만들 수 없음) 이에 Laplace 근사 즉 조금 더 유연한 학습에 적합하며 Ridge 회귀에 사용된다.
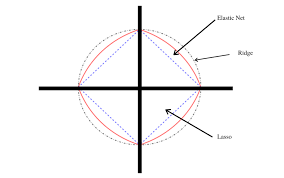
- L1 Norm과 L2 Norm의 경우 각각 기하학적으로 마름모와 원의 형태로 나타나기 때문에, L1의 경우 미분이 불가능한 점이 존재하고, L2의 경우 미분이 불가능한 점이 존재하지 않는다. 이에 딥러닝에서는 주로 규제항의 역할로 L2 Norm이 사용되게 된다.(라그랑주 승수법 관점)
- 번외로 Elastic Net의 경우 L1과 L2를 모두 사용하는 방식으로, 따라서 원 또한 마름모와 원의 중간의 모양을 갖게된다. (두 가지 특성을 모두 가짐)
04. 두 벡터 사이의 거리 및 각도 계산 방법
- L1과 L2 norm을 사용하면 두 벡터 사이의 거리를 다음과 같은 식으로 구할 수 있다. 먼저 두 벡터의 뺄셈을 구한 뒤 구하고자 하는 norm에 따라 거리를 계산해주면 된다.
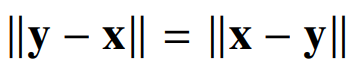
- L2 norm을 사용하면 두 벡터 사이의 각도를 계산할 수 있다. 다음과 같이 분자로 두 벡터의 내적을 구하고, 분모로 각 벡터의 L2 norm의 값을 구해 곱합으로써 코사인 세타 값을 구한 후 두 벡터 사이의 각도를 계산할 수 있다.
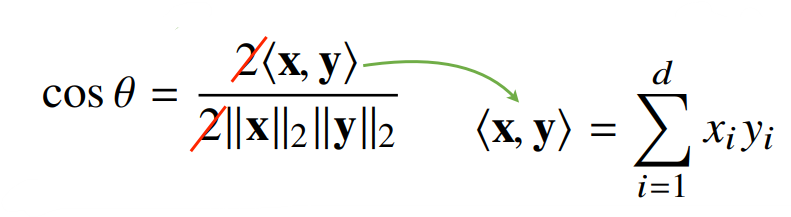
- 두 벡터 사이의 각도를 구할 수 있다는 것은 두 벡터가 서로 얼마나 가까운지 (유사한지)를 알 수 있다는 것 이므로 중요한 개념이다. 아마 추후에 코사인 유사도를 구하는 법을 배울 것이며, 코사인 유사도는 두 벡터가 얼마나 유사한지를 나타내는 방법으로 많이 쓰인다.(추천시스템에서 많이 활용됨)
05. 벡터의 내적
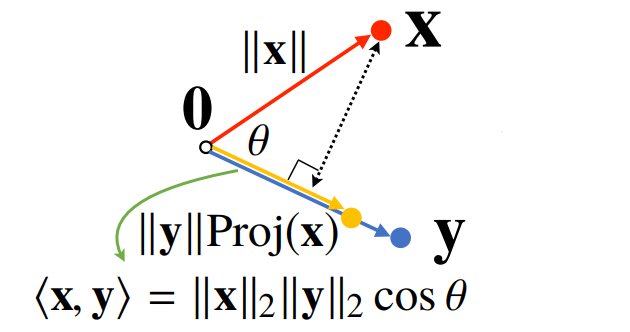
- 벡터의 내적은 정사영(orthogonal projection)된 벡터의 길이와 관련이 있다.
- 내적은 두 벡터의 유사도를 축정하는데 사용할 수 있으며, 우리가 앞으로 다룰 NLP Task의 Attention 기법 또한 내적 유사도가 주로 사용되는 방법이며, 내적 유사도는 코사인 유사도와 비슷하게 두 벡터의 유사도를 측정하는데 사용할 수 있는 아주 좋은 방법 중 하나이다.
참고자료
- http://www.aitimes.kr/news/articleView.html?idxno=17314
- http://taewan.kim/post/norm/
- https://untitledtblog.tistory.com/96
- https://datascienceschool.net/02%20mathematics/05.02%20%EC%A0%9C%ED%95%9C%EC%A1%B0%EA%B1%B4%EC%9D%B4%20%EC%9E%88%EB%8A%94%20%EC%B5%9C%EC%A0%81%ED%99%94%20%EB%AC%B8%EC%A0%9C.html
- https://light-tree.tistory.com/125
