CNN 첫걸음

이번 강에서는 CNN의 기초에 대하여 학습을 진행했다. CNN은 이미지, Sequence 데이터(음성, 텍스트, 시계열, 영상 등) 등 다양한 데이터에 활용되고 있는 딥러닝 모델의 한 종류로, 이미 많이 활용되고 있는 알고리즘이기 때문에 기본 원리에 대한 이해는 필수라고 할 수 있다. 이번 강의를 통해서 CNN에 대한 기초를 완벽히 다지기 위해 노력했다.

00. 공부 내용

• Convolution 연산에 대하여 공부
• Convolution 연산의 역전파에 대하여 공부

01. Convolution 연산

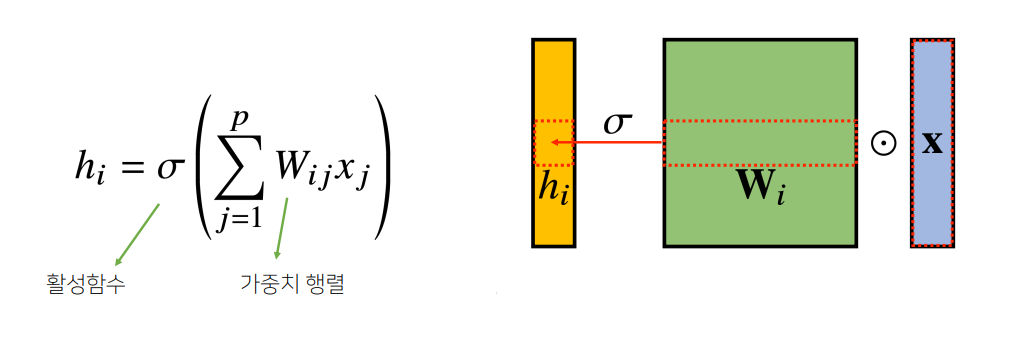
• 지금까지 우리가 배운 MLP 구조는 위와 같이 각 뉴런들이 선형모델과 활성화함수로 모두 연결된 Fully Connected 구조였다.
• 따라서 MLP의 경우 1개의 Layer에 대한 파라미터의 수는 입력벡터의 차원 X 노드의 개수(W의 차원의 수) + bias(노드의 개수)라고 볼 수 있다.

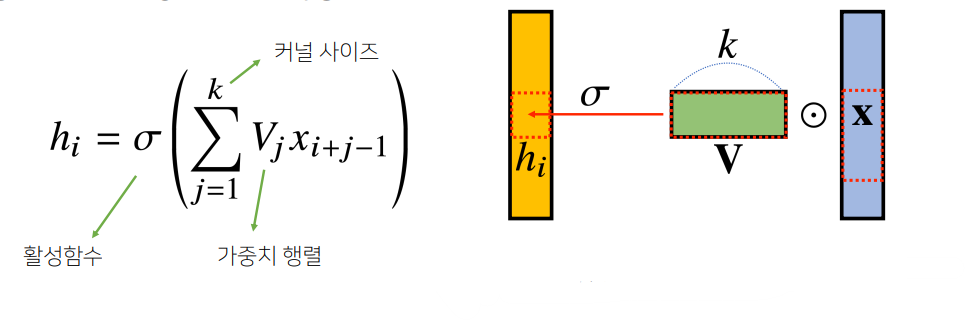
• Convolution 연산은 위와 같이 Kernel을 입력벡터 상에서 움직여 가면서 활성화함수가 적용되는 구조이다.(동일한 커널안에서 가중치를 공유한다고 볼 수 있다.)

• Convolution 연산은 연속형 or 이산형 확률 변수에 따라서 위와 같은 수식으로 전개되며, 신호를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링 한다는 수학적 의미를 지닌다.
• 또한 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용한다.

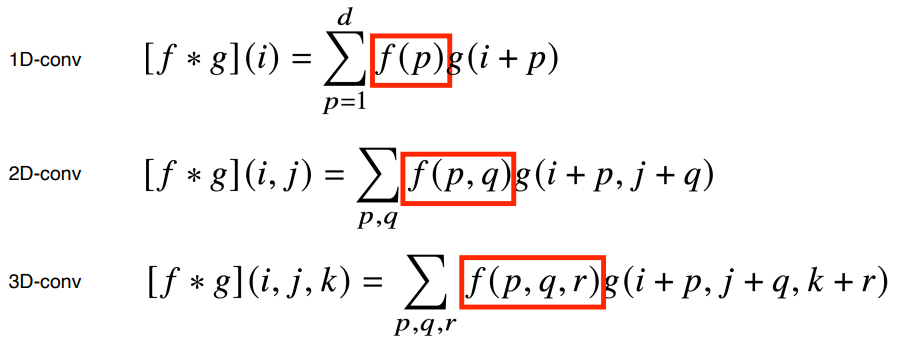
• CNN의 Convolution 연산은 데이터의 차원에 따라서 위와 같은 수식으로 전개된다.

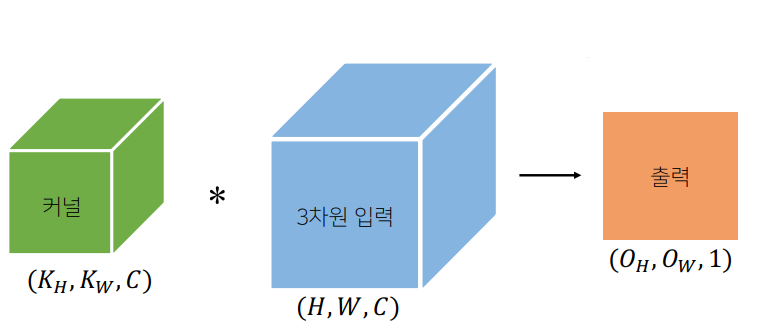
• 채널이 여러개인 2차원 입력의 경우를 예를 들면 위와 같은 2차원 Convolution 연산을 거쳐서 stride 1을 기준으로 인풋벡터의 사이즈 - 커널의 사이즈 + 1의 크기를 가지는 아웃풋 feature map이 생성되게 된다.
• 따라서 CNN의 경우 1개의 Layer에 대한 파라미터의 수는 커널의 사이즈 X 입력벡터에 차원의 수 X 커널의 개수 + bias(커널의 개수)라고 볼 수 있다. (CNN1D의 경우 커널의 사이즈는 i, CNN2D의 경우 커널의 사이즈는 i x j, CNN3D의 경우 커널의 사이즈는 i x j x k)

02. Convolution 연산의 역전파

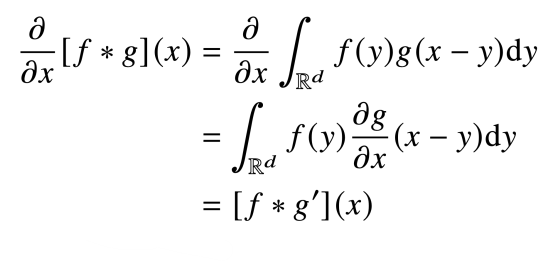
• Convolution 연산은 위와 같은 수식으로 역전파가 계산된다.

• Convolution 연산의 역전파에서 중요한 점은, 결국 Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 위와 같이 Convolution 연산의 형태로 그레디언트가 계산된다는 것이다.