Item2Vec and ANN

00. 학습 내용

• Item2Vec에 대하여 학습
• Approximate Nearest Neighbor에 대하여 학습

01. Item2Vec

1) Word2Vec

(1) 개요

• Word2Vec은 텍스트 분석을 위해 단어(Word)를 벡터로 나타내기 위한 학습 모델, 즉 단어를 Embedding으로 표현하는 모델이라고 할 수 있음
• 여기서 Embedding은 주어진 데이터를 낮은 차원의 벡터(vector)로 만들어서 표현하는 방법을 말함
• Embedding 방법은 크게 Sparse Representation과 Dense Representation으로 나뉨
  • Sparse Representation
    • 아이템의 전체 가짓수와 차원의 수가 동일한 Representation 방법(one-hot encoding 또는 multi-hot encoding)
    • 아이템 개수가 많아질수록 벡터의 차원은 한없이 커지고 공간이 낭비됨
  • Dense Representation
    • 아이템의 전체 가짓수보다 훨씬 작은 차원으로 나타내는 Representation 방법 (Word2Vec 등, 대부분의 DNN 모델은 학습을 통해서 데이터로 부터 Dense Representation을 뽑아내는 것이 목표라고 할 수 있음)
    • 공간의 낭비가 발생하지 않음, 그러나 차원 자체가 하이퍼 파라미터라고 할 수 있음
• Word2Vec을 이용해 구한 Word Embedding은 단어 간 의미적인 유사도 계산에 사용됨(비슷한 의미를 가진 단어일수록 embedding vector가 가까운 위치에 분포)

(2) 학습 방법

Word2Vec의 학습 방법은 크게 Continuous Bag of Words(CBOW), Skip-Gram, Skip-Gram with Negative Sampling 으로 나뉘어짐

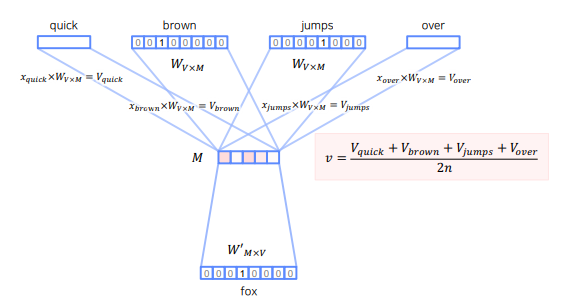
• Continuous Bag of Words(CBOW)는 주변 단어를 가지고 중심 단어를 예측하는 방법
• 즉, 주변 단어를 이용해 구한 벡터로 중심 단어를 맞추는 Multi label classfication 문제를 푸는 것
• 따라서 loss 함수로는 cross entropy를 사용
• 학습 해야 할 파라미터는 단어를 벡터화 시키는 $W_{VM}$ 와 벡터화된 단어로 해당 단어를 예측하는 $W_{MV}$ 총 2개가 필요함
• 앞 뒤로 몇 개의 단어를 사용할 것인지가 중요한 하이퍼라미터 (window)
• window size가 n이라면 중심 단어를 기준으로 앞 뒤로 2n개를 사용함

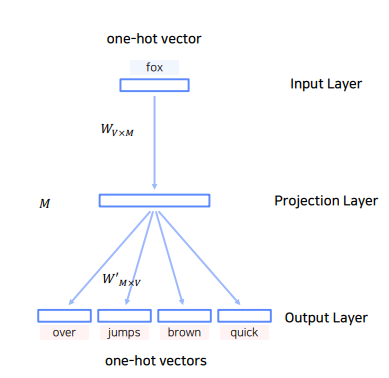
• Skip-Gram은 중심 단어를 가지고 주변 단어를 예측하는 방법
• 즉 CBOW의 반대 버전이라고 생각하면 됨
• 각 예측 단어의 loss 값을 다 더하여 모델을 학습시킴

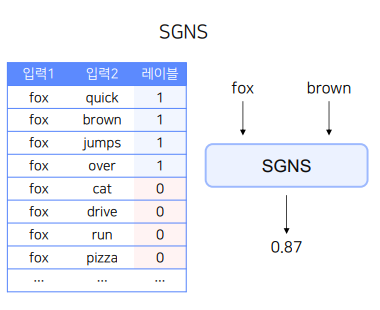
• Skip-Gram with Negative Sampling은 Skip-Gram과 동일하게 중심 단어와 주변 단어를 사용하는 것은 똑같으나, 중심 단어와 주변 단어가 서로 같이 존재하는지의 여부를 1과 0으로 두어 binary classification 문제를 품
• 즉, 주변 단어와 중심 단어가 같이 존재할 확률을 구하는 binary classification 문제라고 할 수 있음
• 따라서 loss 함수로는 binary cross entropy를 사용
• 학습 해야 할 파라미터는 중심 단어를 벡터화 시키는 $W1_{VM}$ 와 주변 단어를 벡터화 시키는 $W2_{VM}$ 와 구해진 두 벡터의 내적 값으로 해당 단어를 예측하는 $W_{MV}$ 총 3개가 필요함
• 따라서 구해진 단어의 embedding lookup tabledms 2개 이기 때문에 선택적으로 하나만 사용하거나 평균을 사용함
• positive sample(중심 단어) 하나당 k개의 Negative Sampling을 진행함(학습 데이터가 적은 경우 5-20, 충분히 큰 경우 2-5가 적당)
• Negative Sample은 중심 단어의 주변 단어에 존재하지 않는 단어들을 의미함

2) Item2Vec

(1) 개요

• Item2Vec은 SGNS에서 영감을 받아 아이템 기반 CF(IBCF)에 Word2Vec을 적용한 방법
• 단어가 아닌 추천 아이템을 Word2Vec을 사용하여 임베딩
  • 기존 MF도 유저와 아이템을 임베딩하는 방법임
• 유저가 소비한 아이템 리스트를 문장으로, 아이템을 단어로 가정하여 Word2Vec 사용
  • Item2Vec은 유저-아이템 관계를 사용하지 않기 때문에 유저 식별 없이 세션 단위로도 데이터 생성 가능
• SGNS 기반의 Word2Vec을 사용하여 아이템을 벡터화하는 것이 최종 목표

(2) 학습 방법

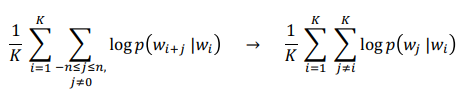
• 유저 혹은 세션 별로 소비한 아이템 집합을 생성
  • 시퀀스를 집합으로 바꾸면서 공간적/시간적 정보는 사라짐(만약 시퀀스를 시간 단위로 스플릿 한다면 시간적 정보도 반영할 수도 있을 것이라고 생각함)
  • 대신 집합 안에 존재하는 아이템은 서로 유사하다고 가정
• 기존의 Skip-Gram이 주어진 단어 앞뒤로 n개의 단어를 사용한 것과 달리 모든 단어 쌍을 사용함(window size를 최대로 한다는 것)
  • 공간적 정보를 무시하므로 동일한 아이템 집합 내 아이템 쌍들은 모두 SGNS의 Positive Sample이 됨
• Skip-Gram with Negative Sampling 방식으로 모델을 학습

(3) 성능

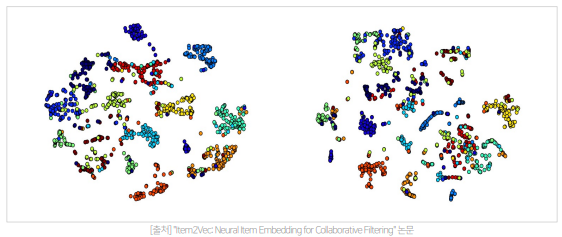
• Item2Vec Embedding(왼)과 SVD Embedding(오)의 t-SNE를 아용한 2차원 시각화 결과 Item2Vec이 더 성능이 좋다는 것을 알 수 있음

02. Approximate Nearest Neighbor

1) 개요

• 만약 우리가 MF 모델을 가지고 추천 아이템을 서빙한다고 했을 때, 해당 유저 Vector와 후보 아이템 Vector들의 유사도 연산이 필요한데, 여기서 후보 아이템이 100만개이고 차원이 100이라고 가정했을 때 Brute Force 방법으로 모든 Vector의 NN을 구하기 위해서는 약 46 시간이 소요됨
• 따라서 효과적이고 효율적인 서빙을 위해서는 모든 Vector에 대한 연산을 계산하는 것 보다 정확도를 조금 포기하더라도 아주 빠른 속도로 주어진 Vector의 근접 이웃을 찾는 것이 더 중요함
• 여기서 사용되는 알고리즘이 바로 Approximate Nearest Neighbor임
• Approximate Nearest Neighbor는 Vector Space Model에서 내가 원하는 Query Vector와 가장 유사한 Vector를 찾는 알고리즘

2) 기법

(1) ANNOY

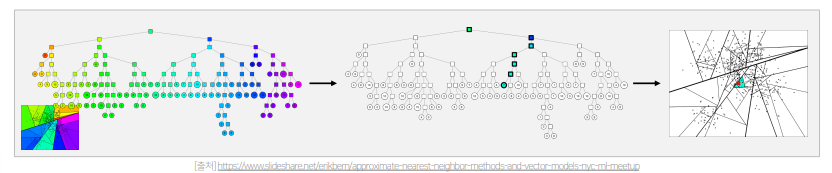
• ANNOY는 spotify에서 개발한 tree-based ANN 기법
• 주어진 벡터들을 여러 개의 subset으로 나누어 tree 형태의 자료 구조로 구성하고 이를 활용하여 탐색
  • 1) Vector Space에서 임의의 두 점을 선택한 뒤, 두 점의 사이의 hyperplane로 Vector Space를 나눔
  • 2) Subspace에 있는 점들의 개수를 node로 하여 binary tree 생성 혹은 갱신
  • 3) Subspace 내에 점이 K개 초과로 존재한다면 해당 Subspace에 대해 1)과 2) 진행
  • 4) ANN를 구하기 위해서는 현재 점을 binary tree에서 검색한 뒤 해당 subspace에서 NN을 search
• number_of_trees(생성하는 binary tree의 개수), search_k(NN을 구할 때 탐색하는 node의 개수) 가 하이퍼 파라미터

(2) Hierarchical Navigable Small World Graphs (HNSW)

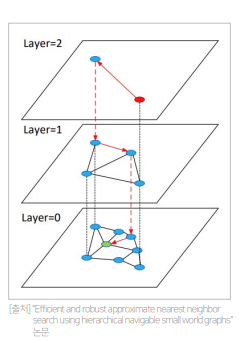
• 벡터를 그래프의 node로 표현하고 인접한 벡터를 edge로 연결하는 방식 (대표 라이브러리는 nmslib, faiss 등이 존재)
  • Layer를 여러 개 만들어 계층적으로 탐색을 진행하여 search 속도 향상
  • Layer 0에 모든 노드가 존재, 최상위 Layer로 갈수록 개수가 적음 (랜덤 샘플링)
• 작동 방식
  • 1) 최상위 Layer의 임의의 노드에서 시작
  • 2) 현재 Layer에서 타겟 노드와 가장 가까운 노드로 이동
  • 3) 현재 Layer에서 더 가까워 질 수 없다면 하위 Layer로 이동
  • 4) 타겟 노드에 도착할 때까지 2)와 3) 반복
  • 2) ~ 4)를 진행할 때 방문했던(traverse) 노드들만 후보로 하여 NN을 탐색

(3) Inverted File Index (IVF)

• clustering을 활용하는 방식
• 작동 방식
  • 1) 주어진 vector를 clustering을 통해 n개의 cluster로 나눠서 저장
  • 2) vector의 index를 cluster별 inverted list로 저장
  • 3) query vector에 대해서 해당 cluster을 찾고, 해당 cluster의 invert list 안에 있는 vector들 대해서 탐색
• 탐색해야 하는 cluster 개수를 증가시킬수록 정확도는 상승하지만 속도는 느려짐(trade-off 관계)

(4) Product Quantization - Compression

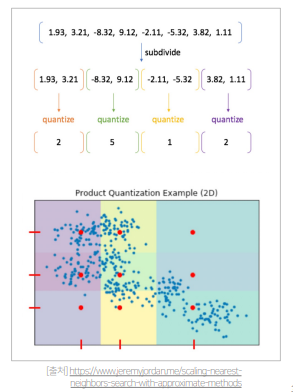
• clustering의 중심 대표값을 활용하는 방식
  • 1) 기존 vector를 n개의 sub-vector로 나눔
  • 2) 각 sub-vector 군에 대해 k-means clustering을 통해 centroid를 구함
  • 3) 기존의 모든 vector를 n개의 centroid로 압축해서 표현
  • 미리 구한 centroid와 target vector의 유사도를 계산하여 sub-vector 군을 구하고 탐색을 진행