그래프 패턴

boostcourse에서 제공하는 그래프와 추천시스템 그래프 패턴에 대한 강의 내용을 정리했다.

00. 학습 내용

• 랜덤 그래프에 대하여 학습
• 그래프의 구조적 특성에 대하여 학습
  • 작은 세상 효과(Small-world Effect)
  • 연결성의 두터운 꼬리 분포(Heavy Tail)
  • 거대 연결 요소(Giant Connected Component)
  • 높은 군집 계수

01. 랜덤 그래프

• Real Graph는 다양한 복잡계로 부터 얻어진 그래프를 의미(현실의 그래프)
  • 소셜 네트워크, 전자상거래 구매 내역, 인터넷, 웹, 지식 그래프 등

• Random Graph는 확률적 과정을 통해 생성된 그래프를 의미(추후에 그래프 간의 유사성을 파악할 때 사용되는 것으로 암)
  • 본 강의에서 다룬 Random Graph는 에르되스-레니 랜덤 그래프
  • 임의의 두 정점 사이에 간선이 존재하는 여부는 동일한 확률 분포에 의해 결정됨
  • 에르되스-레니 랜덤그래프 G(n,p)
    • n개의 정점
    • 임의의 두 개의 정점 사이에 간선이 존재할 확률은 p
    • 정점 간의 연결은 서로 독립적

02. 그래프의 구조적 특성

(1) 작은 세상 효과(Small-world Effect)

작은 세상 효과을 이해하기 위해서는 필수적으로 그래프의 경로, 거리 및 지름에 대한 개념을 이해해야 함

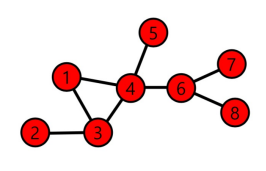
• 정점 u와 v의 사이의 경로(path)는 아래의 조건을 만족하는 정점들의 순열(Sequence)
  • u에서 시작해서 v에서 끝나야함
  • 순열에서 연속된 정점은 간선으로 연결되어 있어야 함
  • ex) 정점 1과 8 사이의 경로
    • 1, 4, 6, 8
    • 1, 3, 4, 6, 8
    • 1, 4, 3, 4, 6, 8

• 경로의 길이는 해당 경로 상에 놓이는 간선의 수로 정의
  (순열의 정점의 수 - 1)
  • 1, 4, 6, 8 -> 3
  • 1, 3, 4, 6, 8 -> 4
  • 1, 4, 3, 4, 6, 8 -> 5

• 정점 u와 v의 사이의 거리(Distance)는 u와 v사이의 최단 경로의 길이
  • ex) 정점 1과 8 사이의 최단 경로
    • 1, 4, 6, 8 -> 길이 3 -> 따라서 거리 3

• 그래프의 지름(Diameter)은 정점 간 거리의 최댓값
  • 본 그래프의 최단 경로의 길이 집합 중 최대의 거리를 가지는 집합은 2, 3, 4, 6, 8 따라서 본 그래프의 지름은 4

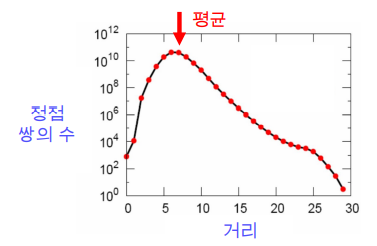
(MSN 메신저 그래프의 정점간 거리, 단 거대 연결 구조만 고려한 경우)

• 작은 세상 효과(Small-world Effect)는 Real Graph에서 임의의 두 정점 사이의 거리는 작다라는 것
• 작은 세상 효과는 높은 확률로 Random Graph에도 존재

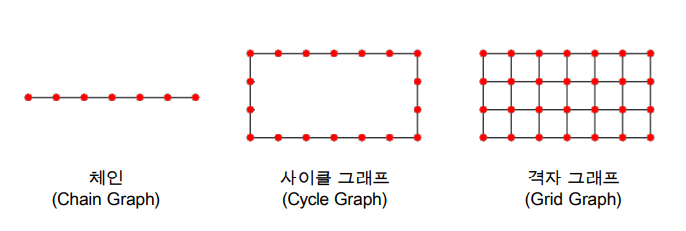
• 하지만 모든 그래프에서 작은 세상 효과가 존재하는 것은 아님
• 위 그래프들은 그래프 크기가 커질 수록 정점 간 거리도 커짐

(2) 연결성의 두터운 꼬리 분포(Heavy Tail)

연결성의 두터운 꼬리 분포를 이해하기 위해서는 연결성에 대한 개념을 이해해야 함

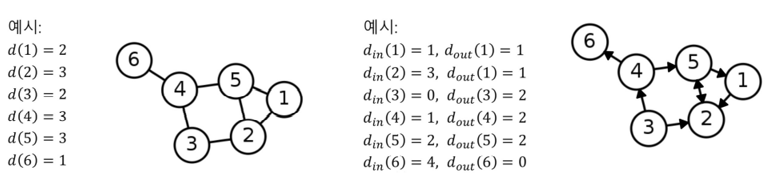
• 정점의 연결성(Degree)은 그 정점과 연결된 간선의 수를 의미
• 정점의 Out Degree는 그 정점에서 나가는 간선의 수를 의미
• 정점읜 In Degree는 그 정점으로 들어오는 간선의 수를 의미

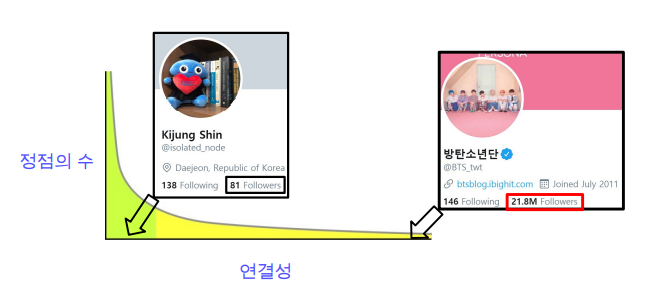
• 실제 그래프의 연결성 분포는 Heavy Tail 분포를 가짐
• 즉, 연결성이 매우 높은 허브(Hub) 정점이 존재함을 의미

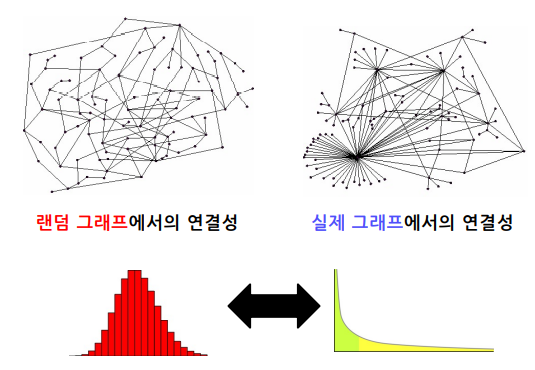
• 랜덤 그래프의 연결성 분포는 높은 확률로 정규 분포와 유사
• 즉, 연결성이 매우 높은 허브(Hub) 정점이 존재할 가능성은 0에 가까움

(3) 거대 연결 요소(Giant Connected Component)

거대 연결 요소를 이해하기 위해서는 연결 요소에 대한 개념을 이해해야 함

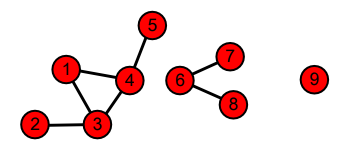
• 연결 요소(Connected Component)는 다음 조건들을 만족하는 정점들의 집합을 의미
  • 연결 요소에 속하는 정점들은 경로로 연결될 수 있어야 함
  • 위의 조건을 만족하면서 정점을 추가할 수 없어야 함
  • ex) 위 그래프의 경우 {1, 2, 3, 4, 5}, {6, 7, 8}, {9}로 총 3개의 연결 요소가 존재

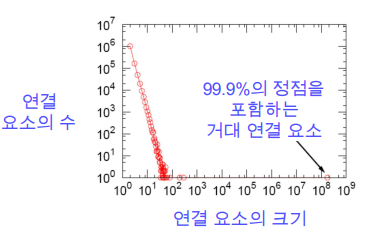
• Real Graph에는 거대 연결 요소(Giant Connected Component)가 존재
• 겨대 연결 요소는 대다수의 정점을 포함함
• MSN 메신저 그래프이 경우 99.9%의 정점이 하나의 거대 연결 요소에 포함됨

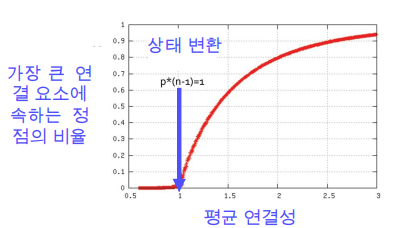
• Random Graph에도 높은 확률로 거대 연결 요소(Giant Connected Component)가 존재
• 단, 정점들의 평균 연결성이 1보다 충분히 커야함

(4) 높은 군집 계수

군집 계수를 이해하기 위해서는 군집, 지역적 군집 계수, 전역 군집 계수에 대한 개념을 이해해야 함

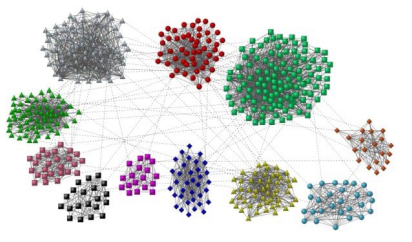
• 군집(Community)이란 다음 조건들을 만족하는 정점들의 집합을 의미
  • 집랍에 속하는 정점 사이에는 많은 간선이 존재
  • 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재
  • 위는 수학적인 엄밀한 정의는 아님
  • 예시 그래프의 경우 11개의 군집이 존재하는 것으로 판단됨

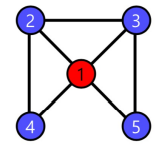
• 지역적 군집 계수(Local Clustering Coefficient)는 한 정점에서 군집의 형성 정도를 측정하는데 사용됨
• 정점 i의 지역적 군집계수는 정점 i의 이웃 쌍 중 간선으로 직접 연결된 것의 비율을 의미
• 정점 i의 지역적 군집 계수는 $c_{i}$로 표현
• ex) 정점 1의 이웃 쌍 = (2,3), (2,4), (2,5), (3,4), (3,5), (4,5) = 6 // 정점 1의 이웃 쌍 중 간선으로 직접 연결된 것 = (2,3), (2,4), (3,5) = 3 // $c_{1}$ = 3 / 6 = 0.5
• 연결성이 0인 정점에서는 지역적 군집 계수가 정의되지 않음
• 정점 i의 지역적 군집 계수가 매우 높음 -> 정점 i의 이웃들도 높은 확률로 서로 간선으로 연결되어 있음 -> 정점 i와 그 이웃들은 높은 확률로 군집을 형성함

• 전역 군집 게수(Global Clustering Coefficient)는 전체 그래프에서 군집의 형성 정도를 측정하는데 사용됨
• 그래프 G의 전역 군집 계수는 각 정점에서의 지역적 군집 계수의 평균값
• 단, 지역적 군집 계수가 정의되지 않는 정점은 제외

• Real Graph에서는 군집 계수가 높음 -> 즉 많은 군집이 존재함
  • 동질성: 서로 유사한 정점끼리 간선으로 연결될 가능성이 높음
  • 전이성: 공통 이웃이 있는 경우, 공통 이웃이 매개 역할을 해줄 수 있음

• Random Graph에서는 지역적 혹은 전역 군집 계수가 높지 않음
  • G(n,p)에서 군집 계수는 p임
  • 각 정점은 서로 독립적이라는 가정을 세우고 있기 때문에, Real Graph의 동질성, 전이성 이라는 특징을 가질 수 없음