Gradient Descent

• 기울기 하강
• Cost Function J의 최솟값을 구하는 알고리즘

want

함수 J의 세타값을 최소화 하는 것

Gradient descent algorithm

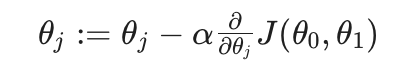
위의 식을 이용하여 세타를 구한다.

Definition Meaning

:= vs =

• :=

  • 할당 기호

  • ex) a:= b
    컴퓨터에서 b의 값을 a에 대입한다는 의미
    a := a+1 --> 가능

• =

  • "참" 을 의미
  • ex) a = b
    a 값이 b와 같다
    a = a+1 --> 불가능

α

• learning rate
• 얼마나 많은 값이 변하는가에 대한 변수
• parameter J값이 영향을 받음

Correct vs Incorrect

Correct : Simultaneous update

• 같은 시간에 θ0과 θ1의 값을 바꿈
• temp0와 temp1을 먼저 계산하고 θ0과 θ1에 동시에 값 대입

Incorrect

• temp0 값을 계산 --> θ0 값 변경
• 이후, temp1 계산 --> θ1 값 변경

두 방법에 차이가 생기는 이유

temp0와 temp1를 계산할 때 θ0과 θ1의 값을 이용하여 계산을 해야한다.
만약 incorrect의 방식(θ0 값 변경이 먼저 일어난 경우)을 이용하여 계산한 경우, temp1을 계산할 때 바뀐 θ0의 값을 사용하게 되기 때문에 결과가 다르게 나타나게 된다.

그러므로 반드시 Simultaneous update 방식을 사용하도록 해야한다.

Gradient Descent Intuition

• α : learning rate
• d/dθ•J(θ0,θ1) : 미분계수

미분계수

미분계수가 하는 일 --> 그 점의 탄젠트 값(기울기)을 구하는 것

미분계수가 양수인 경우

d/dθ•J(θ0,θ1) > 0

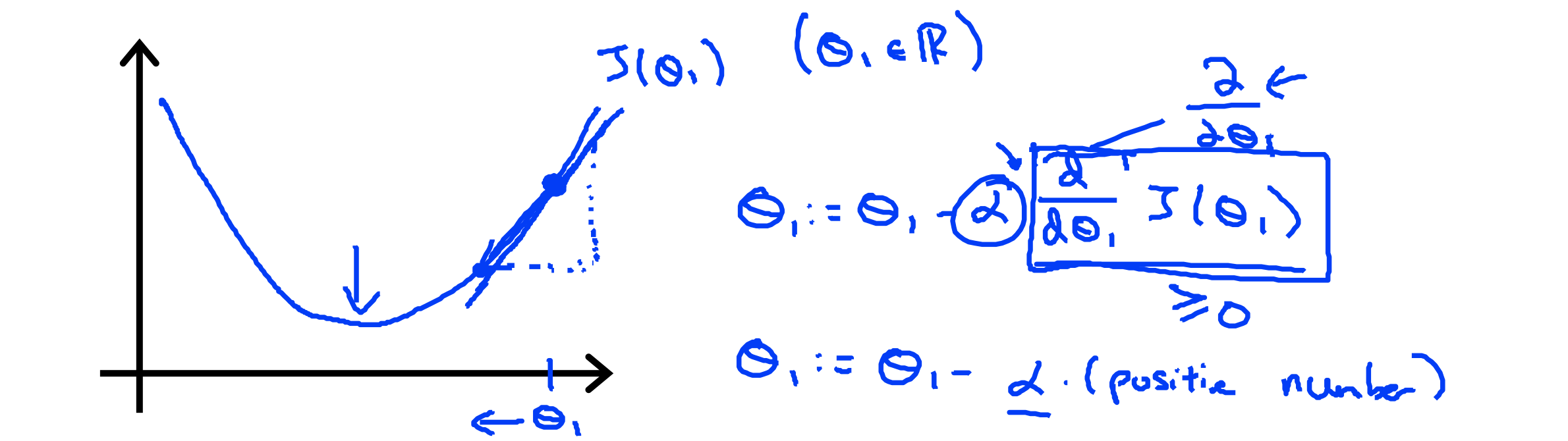
• J(θ1)를 최소화하기 위해 θ1이 감소해야한다

미분계수가 음수인 경우

d/dθ•J(θ0,θ1) < 0

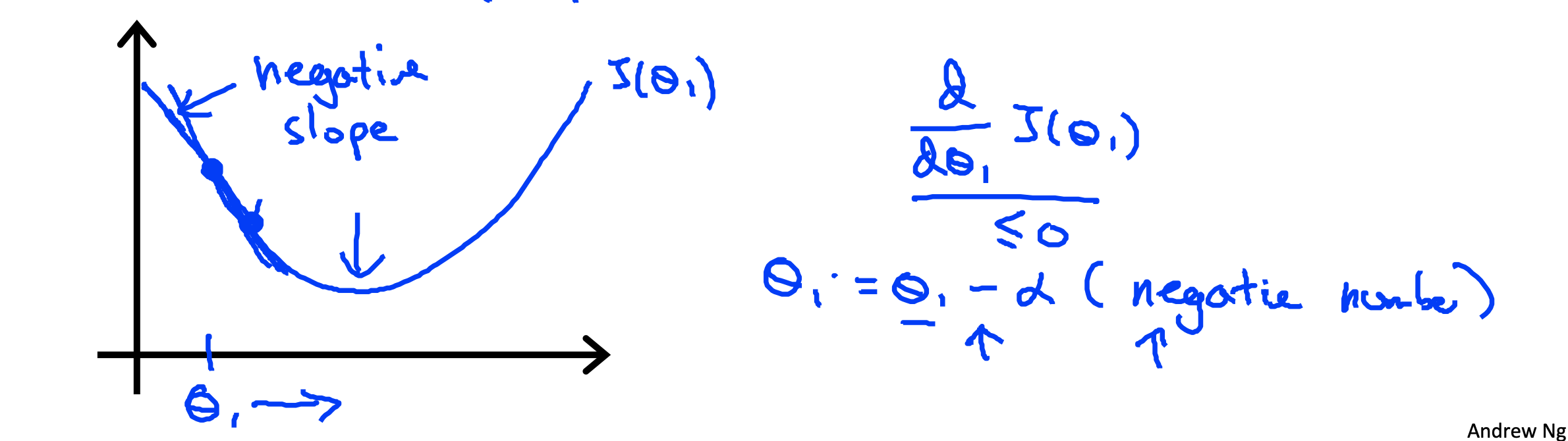
• J(θ1)를 최소화하기 위해 θ1이 증가해야한다

learning rate

α는 한 점의 이동 정도를 의미

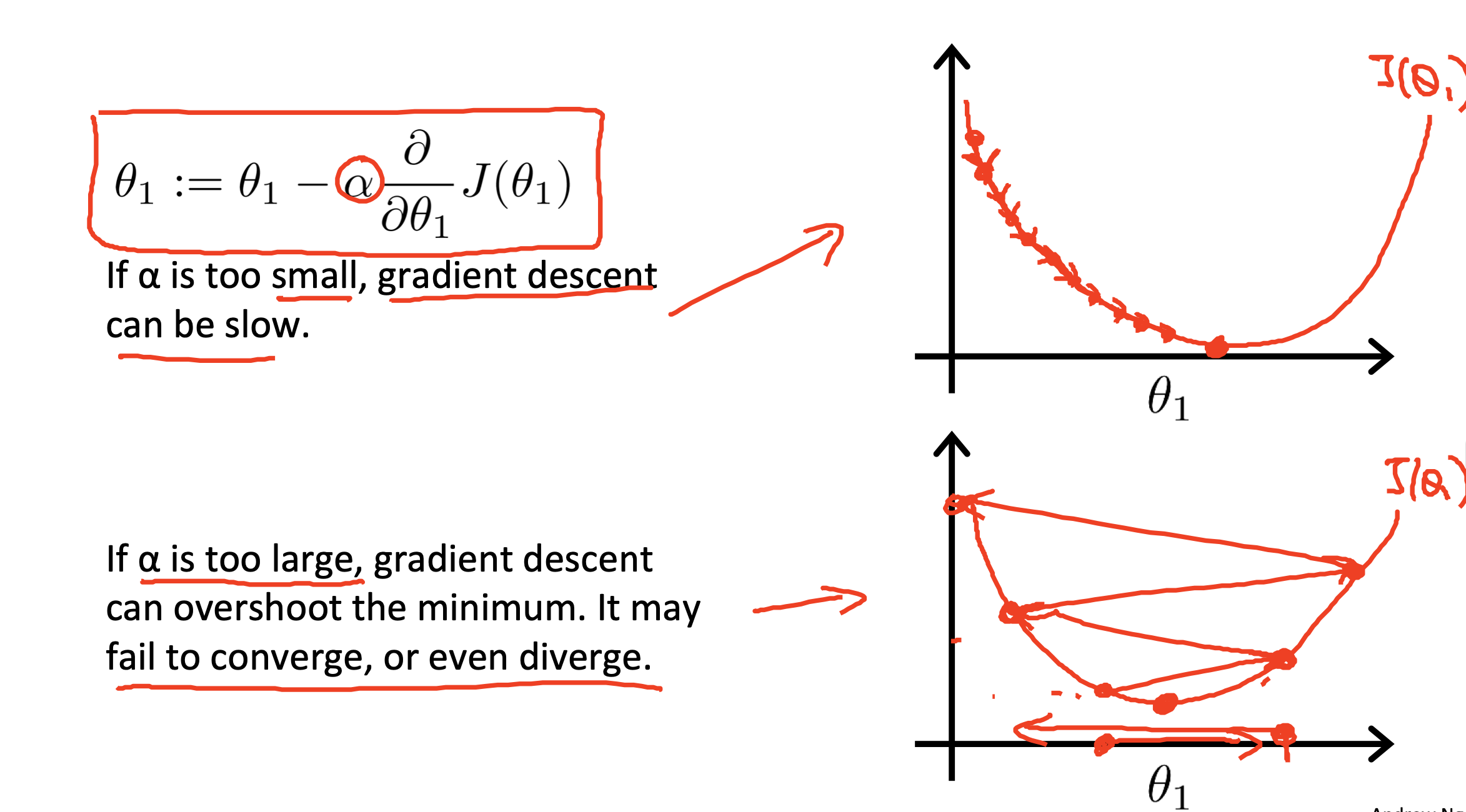
α가 너무 작은 경우

• α가 작으면 θ1의 값이 조금씩 움직여야한다
• 하강이 매우 느려진다
• 많은 이동이 필요

α가 너무 큰 경우

• α가 크면 θ1의 값이 크게 움직여야한다
• 하강이 너무 빨라져서 값을 바꾸거나 방향을 바꾸는 것이 어려워질 수 있다

θ1이 이미 최소값인 경우

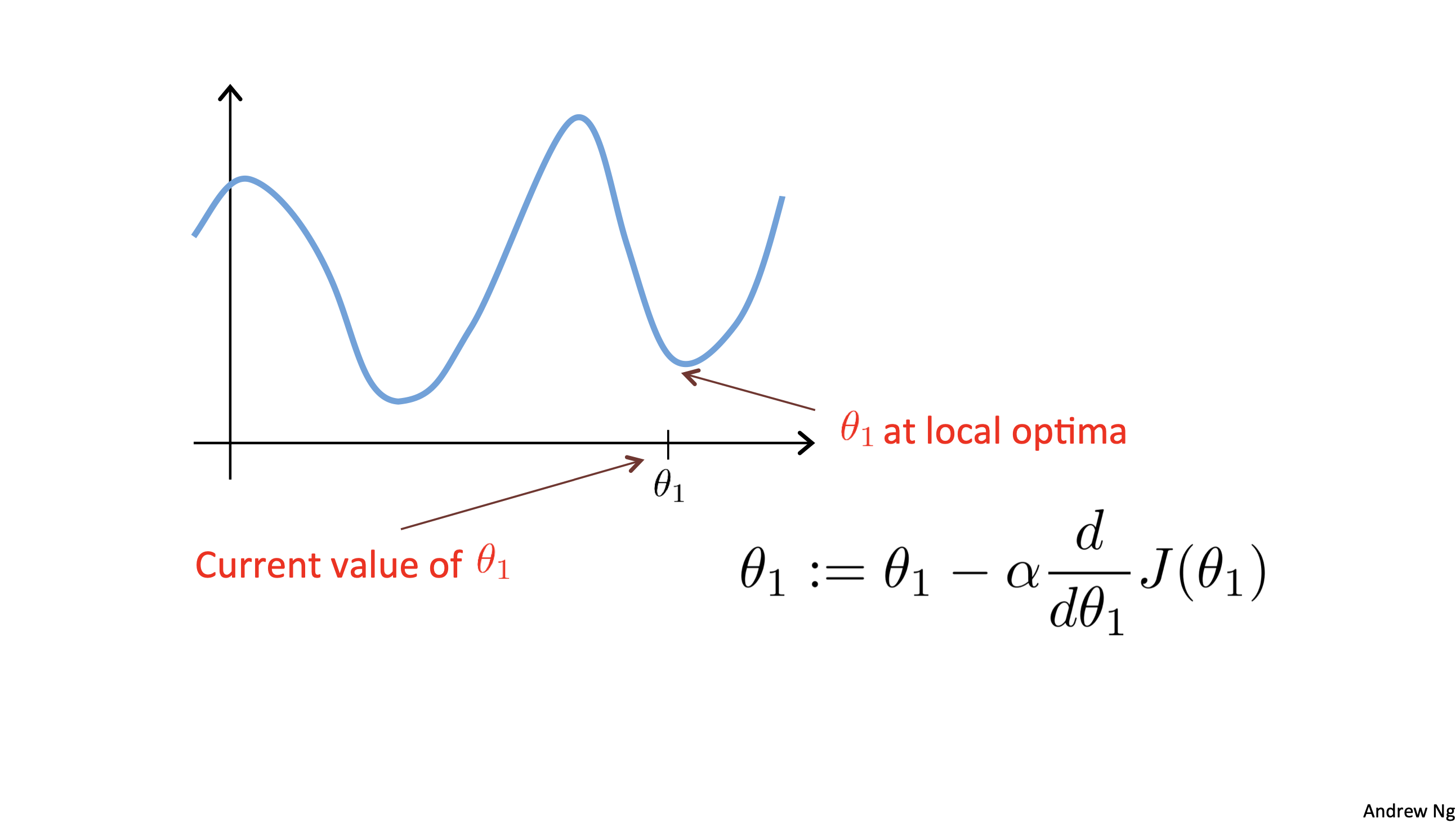
θ1이 이미 최소값인 경우 --> 미분계수가 0이 된다

따라서 θ1 := θ1 - (α • 0) 이므로 θ1 = θ1
이 경우 α 값은 아무런 영향을 주지 않는다

α가 고정값인 경우

α가 고정인 경우 하강 기울기는 최소값에 영향을 미치지 못한다

why?

최소값에 가까워짐에따라 미분계수는 0에 가까워진다
그러므로 최솟값에 가까워짐에 따라 (α • d/dθ•J(θ0,θ1))의 값도 감소하게 된다 --> 즉, 작은 거리를 이동하게 된다

하강 기울기는 최솟값에 가까워질수록 더 작은 거리를 이동하게 되고 결국 최솟값에 도달할 수 있다

Gradient Descent For Linear Regression

want

기울기 하강을 사용해서 비용함수 차의 제곱을 최소화하는 것

식 1

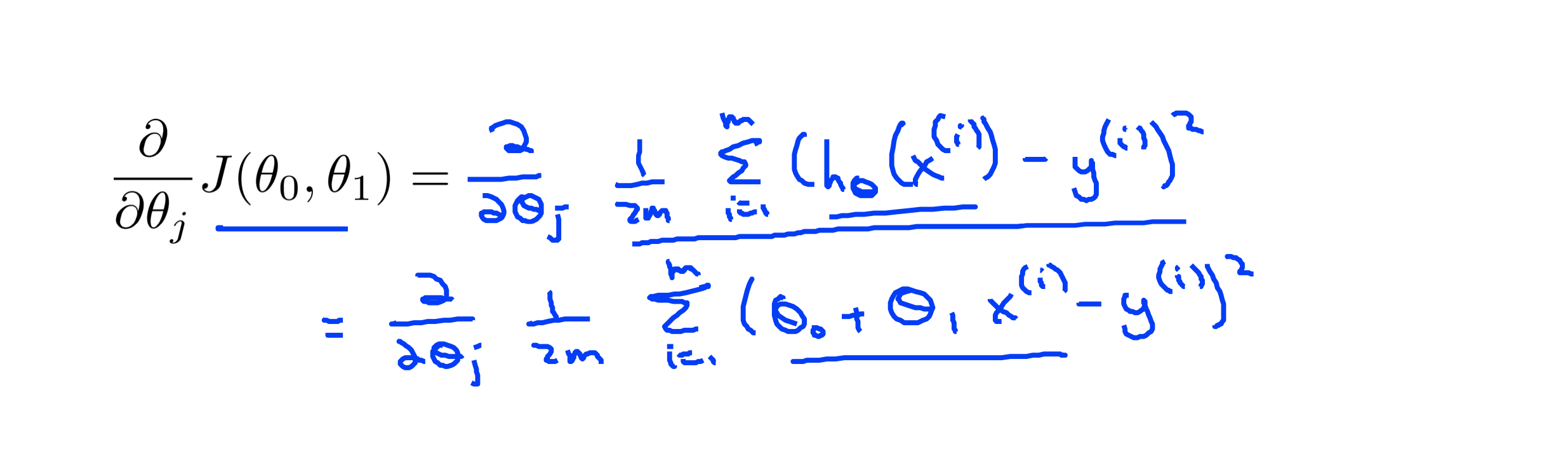
위의 식은 미분계수의 J함수 부분에 Cost Function의 J를 대입한 것

식 2

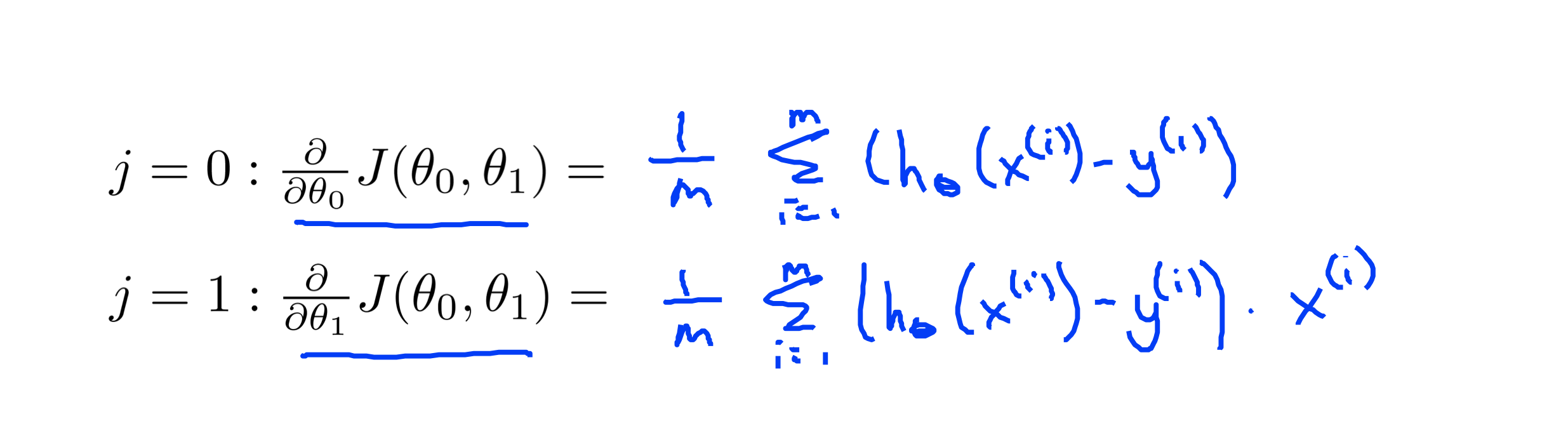
• j = 0 --> θ0 인 경우