[논문 리뷰] CADE: Detecting and explaining concept drift samples for security applications

안녕하세요. 오늘은 CADE: Detecting and explaining concept drift samples for security applications에 대해 리뷰해보겠습니다.

본 논문은 제목에서 알수 있듯이 concept drift를 탐지하고 explaning까지 하는 방법도 소개하는 논문입니다.

explanation이 필요한 이유는 결국 concept drift를 해결하기 위해선 일반적으로 Active Learning이 필요합니다.

즉, Analyst가 직접 concept drift sample에 대해 labeling을 한다는 것입니다.

그렇기 때문에 해당 drift sample이 왜 drift sample인지 explanation을 해주게 된다면 좀 더 빠르게 labeling을 할 수 있게 됩니다.

기존 논문에 비해 본 논문의 contribution은 다음과 같습니다.

• 기존 논문에서는 explanation을 할 때 boundary-based 였던 것에 비해 본 논문에서는 distance-based로 explanation을 합니다.
  (distance-based는 Contrastive Autoencoder Learning을 통해 이루어집니다.)
• learnable한 masking 변수인 m을 통해 important feature을 도출해낼 수 있습니다. 즉, 어떠한 feature때문에 drifting sample로 판별됐는지 설명할 수 있게 됩니다.

1. Introduction

real-world에서 concept drift 현상은 매우 일반적이고 이를 해결하기 위해 많은 연구가 진행중입니다.

real-world에서는 매우 많은 양의 data가 입력될 뿐만 아니라 입력 data의 분포도 시간이 지남에 따라 매우 동적으로 변하기 때문에 이에 대한 해결책이 필요합니다.

본 논문에서는 이를 해결하기 위해 아래와 같은 구조를 제안합니다.

High-Level Idea

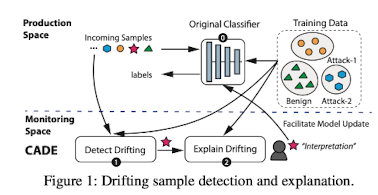
1) Training Dataset을 이용해 Classifier을 훈련합니다.

2) Incoming Samples를 훈련된 Classifier에 입력합니다.

3) Classifier은 drift sample을 탐지하도록 훈련되어 있기 때문에 drift sample을 탐지합니다.

4) drift sample에 대해 explain 하기 위해서 explanation method를 거쳐 가장 중요한 features을 추출합니다.

5) explain 된 정보를 참고하여 Analyst는 lebling을 합니다.

6) labeling된 drift sample을 Training Dataset에 추가합니다.

7) 1번부터 다시 반복합니다.

Original Classifier

위 High-Level Idea의 이미지를 보면 Classifier의 접두사로 Original이 붙은 것을 확인할 수 있습니다.

선행 연구에서는 Classifier(Original Classifier)을 confidence prediction을 하였습니다.

여기서 말하는 confidence prediction은 간단하게 softmax와 같은 활성화 함수로 prediction 했다고 생각하면 될 듯 합니다.

이에 따른 단점은 명확합니다.
Classifier가 0, 1, 2, 3의 class에 대해서 훈련되었다고 했을 때 시간이 지난뒤 새로운 공격 유형인 4가 입력되었다고 가정하겠습니다.

이런 경우 4는 0, 1, 2, 3중에 한 class에 높은 confidence를 갖으며 prediction 될 가능성이 높습니다.

즉, relative fitness 현상이 발생합니다.

Our Method

본 논문에서는 Original Classifier의 문제점을 해결하기 위해 Contrastive Autoencoder을 사용합니다.

1. AutoEncoder은 차원이 축소되며 압축된 표현을 학습하는데 유용합니다.

2. Contrastive Learning은 drifting sample detection과 explanation에 대해 각각의 장점이 있습니다.

• drifting sample detection
  Contrastive Learning의 특성상 drifting sample을 탐지 및 점수를 도출하는데 효과적입니다.
  그 이유는 다른 클래스별로 서로 일정한 거리를 두고 같은 클래스별로는 clustering 되는 특징이 있기 때문에 drifting sample은 그 어느 곳에도 속하지 않고 각 클래스 사이 그 어딘가에 표류해 있을 가능성이 큽니다.
  또한 distance 기반이기 때문에 drifting sample의 점수를 매기는것도 상대적으로 쉽습니다.

• explanation
  기존 논문의 explanation은 supervised learning, softmax 함수 기반이였습니다. 이렇게 되면 단점은 명확합니다.
  Original Classifier 파트에서 설명한 relative fitness 문제 때문에 기존의 클래스 중 한 곳으로 분류됩니다.
  이렇게 되면 새로운 클래스에 대해서는 explanation을 하기 어렵습니다.
  또한, supervised 특성상 각 class 별로 충분한 data가 주어져야 클래스별 분포가 잘 형성 됩니다.
  하지만 real-world 환경에서 클래스별 충분한 data가 주어지는 것은 충족되기 어렵습니다.
  이를 해결하기 위해서 Contrastive Learning을 이용하게 된다면, drifting sample은 기존의 supervised 환경과는 다르게 relative fitness 현상이 비교적 덜합니다.
  즉, 어느 class에도 속하지 않고 표류하게 됩니다.
  이렇게 표류하게 된다면 drifting sample이란 것을 알아차릴 수 있게 되어 explanation이 가능합니다.

실제 본 논문에서 제안하는 Contrastive Autoencoer가 Leatent space에서 압축된 표현을 잘 표현하는지는 아래 이미지에서 확인이 가능합니다.

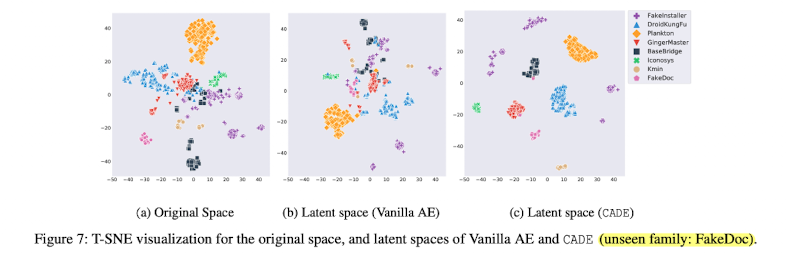
확실히 (c)에서 서로 다른 class끼리 거리가 벌어지면서 같은 class끼리는 뭉치도록 잘 표현이 되고 있는 것을 볼 수 있습니다.

Contribution

1. concept drift에 적합하지 않은 기존의 supervised learning 기반 방식을 보안하기 위해 효과적인 contrastive learning 기법을 소개합니다.

   CADE에서 사용하는 contrastive가 supervised learning이 아니다. 라고는 단정지어 말하지 못하지만 한 가지 확실한 점은 softmax와 같이 relative fitness가 이루어질만한 환경이 아닌 다른 클래스와의 거리 차이를 기반으로 매핑되기때문에 즉, 어느 한 클래스로 분류 개념이 아닌 distance 기반이기 때문에 relative fitness 문제 해결 기여가 더 큽니다.

2. supervised explanation의 한계점을 설명하고, distanced-based explanation 기법을 소개합니다.

2. Method

Contrastive Autoencoder Loss

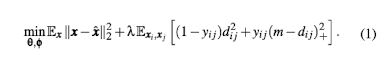
위 (1) 수식은 reconstruction loss와 contrastive loss를 함께 훈련합니다.

1. $\|x-\hat{x}\|_2^2$ 은 reconstruction loss를 의미합니다.
   x는 original input을 의미하며, $\hat{x}$는 decoder에 의해 reconstruction 된 x를 의미합니다.
   또한 두 변수의 차이를 제곱을 해줌으로써 즉, MSE를 통해 학습합니다.

2. $(1-y_{ij})d_{ij}^2 + y_{ij}(m-d_{ij})^2$은 contrastive loss를 의미합니다.
   $y_{ij}$는 주어진 한 쌍의 클래스가 서로 같을 때는 0, 다를 때는 1을 출력합니다.
   $d_{ij}$는 주어진 한 쌍의 클래스간의 거리입니다. 거리 공식으로는 간단하게 유클리드 제 2법칙을 사용합니다.
   m은 서로 다른 클래스끼리 벌어질 거리를 의미합니다.
   $y_{ij}$가 0이 되는 경우에는 1 x $d_{ij}^2$ + 0 x (m - $d_{ij}^2$) => $d_{ij}^2$,
   $y_{ij}$가 1이 되는 경우에는 0 x $d_{ij}^2$ + 1 x (m - $d_{ij}^2$) => 1 x (m - $d_{ij}^2$)가 됩니다.
   다시말해서 주어진 한 쌍의 클래스가 서로 같을 때는 $d_{ij}^2$를 최소화 하는 목표로,
   주어진 한 쌍의 클래스가 서로 다를 때는 1 x (m - $d_{ij}^2$)를 최소화 하는 목표로 훈련 하게됩니다.
   즉, 같은 클래스끼리는 최대한 뭉치도록하며 다른 클래스끼리는 최소 m 만큼 거리가 벌어지도록 합니다.

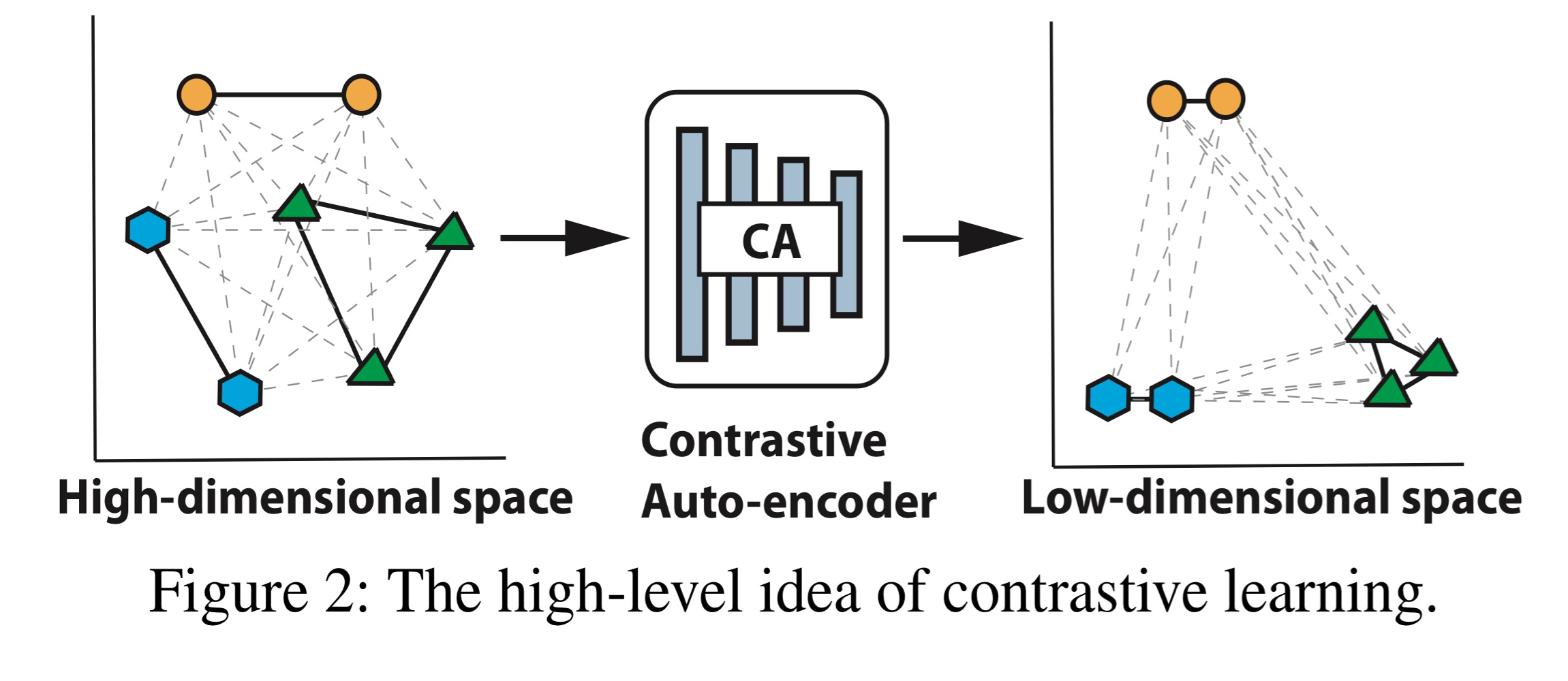
위 이미지는 Contrastive Autoencoder을 수행하며 High-dimension sapce에서 Low-dimension으로의 변환 과정을 나타냅니다.

MAD-based Drifting Sample Detection

Contrastive Autoencoder을 통해 latent space에서 같은 클래스끼린 뭉치게하고 서로 다른 클래스끼린 거리가 벌어지게 하였습니다.

하지만 여기서 추가로 생각해야할 것이 있습니다.
무슨 기준으로 drifting sample을 판단해야할까요?

본 논문에선 MAD(Median Absolute Deviation)를 제안합니다.
MAD에서는 각 클래스의 centroid를 기준으로 각 각의 treshold를 지정해줍니다.

새로 입력된 data가 모든 class의 MAD의 treshold에 벗어나게 된다면 drifting sample로 분류됩니다.

CADE에서의 contribution 중 하나가 decision boundary를 사용하지 않는다. 였는데 위 내용을 보니 결국 MAD가 decision boundary랑 비슷한 개념이라고 느껴질 것입니다. 어느정도 맞는 말입니다. 하지만 명확한 차이는 CADE의 MAD는 단지 drifting sample을 찾는데 사용되고 기존 논문의 decision boundary는 explanation에 사용된다는 점입니다. 즉, CADE의 explanation에서는 decision boundary 개념을 사용하지 않기에, distance 기반으로 explanation을 할 수 있게 되며 softmax 활성화 함수를 사용하지 않기 때문에 relative fitness 문제에 비교적 자유롭습니다.

자세한 알고리즘은 다음과 같습니다.

Line 2-4)
Contrastive Autoencoder을 통해 학습해줍니다.

Line 5)
각 클래스의 centroid를 구합니다.

Line 6-8)
각 클래스에서 본인과 같은 클래스를 갖는 각각의 sample과 centroid의 거리 차이 값을 구합니다.

Line 9)
거리 차이 값의 평균을 $\tilde{d}_i$에 저장합니다. 즉, $\tilde{d}_i$는 i 클래스에서 centroid와 각 샘플간의 거리 차이의 중앙 값을 의미합니다.

Line 10)
각 i 클래스의 샘플과 $\tilde{d}_i$의 차이를 계산하여 median 값을 구합니다.
그리고 constant 값인 b 값을 곱해 i 클래스의 MAD값을 구합니다.
즉 $MAD_i$는 각 클래스 i의 treshold로 생각해주셔도 될 듯 합니다.

Line 14)
test sample이 주어졌을때 latent variable인 z로 인코딩 합니다.

Line 16)
유클리드 거리 법칙을 이용해 test sample과 각 각의 class의 centroid와의 거리를 계산해줍니다.

Line 17)
$A_i^{(k)}$는 $d_i^{(k)} - \tilde{d_i} / MAD_i$를 의미합니다.
$d_i^{(k)}$는 각 i class의 centroid와 test sample간의 거리 차이입니다.
그러므로 $A_i^{(k)}$의 값이 크면 test sample이 i class에 대해 treshold를 넘어 outlier에 존재한다고 볼 수 있습니다.

Line 19)
$A^{(k)}$의 값을 구하는데 $A_i^{(k)}$의 최솟값을 구합니다.
이 의미는 test sample과 가장 가까이 존재하는 class i인 경우에만 생각하겠다는 의미입니다.

Line 20-24)
$A_i^{(k)}$가 $T_{MAD}$보다 더 크면 해당 test sample은 drifting sample로 판단하고
그 반대인 경우에는 non-drifting sample로 판단합니다.
$T_{MAD}$는 3.5로 설정되어있으며 이는 실험적으로 설정하였다고 합니다.

Line 26)
각 i class의 centroid 중 가장 가까운 class를 선택해 test sample의 y 값으로 저장해줍니다.

Explaining Drifting Samples

선행 연구에서는 drifting sample을 explanation 하기 위해 boundary-based Explanation을 하였습니다.
이에 대한 한계점은 다음과 같습니다.

• 제한된 drifting sample을 고려할 때 decision boundary에 정확한 근사 모델을 도출하기가 어렵습니다.
• in-distribution region에 비해 out-distribution의 공간이 매우 큽니다.
  i개의 클래스에 따른 clustring 형성 된 곳을 제외하면 그 외의 모든 영역이 out-distribution입니다.
  그렇기 때문에 drifting sample은 각 각의 클래스가 클러스터링을 형성한 곳으로부터 매우 멀리 떨어져 있을 가능성이 높습니다.
  이런 경우에 매우 멀리 떨어져 있는 drifting sample을 가까운 클래스의 boundary 안에 넣는 것은 매우 어렵습니다.

decision boundary 안으로 들어갈 수 없다면 important feature을 추출하는데 필요한 grad를 구할 수 없습니다.

그래서 본 논문에서는 Boundary-based Explanation이 아닌 Distance-based Explanation을 제안합니다.
Distance-based Explanation의 장점은 다음과 같습니다.

• drifting sample을 explanation 하기 위해서 boundary 안으로 들어갈 필요가 없습니다.
  단지 original feature을 perturb하며 distance change를 관찰하면 됩니다.

Explanation을 하기 위해선 important한 feature을 알아야합니다.
여기서 import한 feature이란 예를들어 feature을 1,000개를 갖는다고 가정하겠습니다.
drifting sample이 탐지되었고 해당 sample이 가장 가까운 클래스와 어떠한 feature에 차이가 있어 drifting sample이 되었는지를 판가름하는 feature을 말합니다.

important feature을 알아내기 위한 공식은 아래와 같습니다.

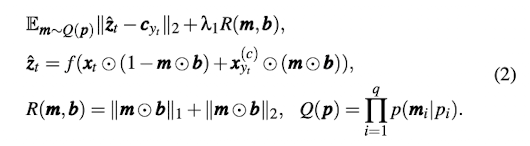
위 수식에서 의미하는 각 요소와 기호는 아래와 같습니다.

• ⊙는 요소별 곱셈을 의미합니다.
• i는 feature의 각 요소를 의미합니다.
• t는 test sample을 의미합니다. (엄밀히 말하면 drifting sample입니다.)
• q는 총 test sample의 개수입니다.
• m은 learnable하며 mask를 의미합니다. 1일시 가장 가까운 클래스에서 centroid와 가장 가까운 샘플의 feature로 대체합니다.
  0일시 drifting sample의 feature을 그대로 유지합니다.
• b는 pre-filter을 의미합니다. 가장 가까운 클래스에서 centroid와 가장 가까운 샘플의 feature가 해당 drifting sample과 값이 같다면 중요하지 않은 feature이므로 제거합니다. 즉, b는 0으로 상정되며 반대의 경우 b는 1으로 상정됩니다.
• $c_{y_t}$는 t sample에 가장 가까운 class의 centroid를 의미합니다.
• $x_{y_t}^{(c)}$는 $c_{y_t}$에서 가장 가까운 샘플을 의미합니다.

첫 번째 텀은 최종적인 수식으로 $c_{y_t}$와 $\hat{z}_t$의 유클리드 2에 의한 거리 차이를 최소화 하는 동시에 $R(m,b)$에 의해 important feature의 개수를 최소화하도록 훈련합니다.

그렇다면 우리는 여기서 $\hat{z}_t$의 의미와 $R(m,b)$ 또한 알아볼 필요가 있습니다.

먼저 $\hat{z}_t$는 purturbed sample을 의미합니다. 다시 말해서 original sample에서 feature을 변경한 샘플의 latent variable을 말합니다. 변경할 feature은 b에 의해서 일차적으로 pre-filter 되며, 그 다음으로 learnable한 m에 의해 결정됩니다.

다음으로 $R(m,b)$는 유클리드 1과 2를 이용한 m의 개수 최소화입니다.
m은 위에서 말씀드렸듯이 mask를 의미하는데 mask를 최대한 많이 적용해서 important feature의 개수를 최소화하는 목표입니다.

mask를 최대한 적용하려는 이유는 고차원의 feature을 갖는 dataset일 시에 훈련 속도가 느릴뿐더러 불필요한 feature의 개입으로 인한 훈련에 방해가 될 수 있기 때문입니다.

즉, mask 개수를 최대화하고 important feature의 개수를 최소화해 훈련적으로 optimal하게 할 수 있도록 도와주는 수식이라고 봐주시면 될 것 같습니다.

두 번째 텀은 첫 번째 텀에서 설명한 $\hat{z}_t$에 대한 상세 설명입니다.

$f$는 인코더를 의미하며,
$f(x_t ⊙ (1 - m ⊙ b) + x_{y_t}^{(c)} ⊙ (m ⊙ b)))$에 의해서 $\hat{z}_t$가 $c_{y_t}$에 최대한 가깝도록 훈련됩니다.

개인적으로 $f(x_t ⊙ (1 - m ⊙ b) + x_{y_t}^{(c)} ⊙ (m ⊙ b)))$에서 궁금했던게 $f(x_t ⊙ (m ⊙ b))$로만 해주어서 $c_{y_t}$에 최대한 가깝게 해주면 되는게 아닌가? 싶었습니다.

본 논문에도 이에 대한 설명은 나와있지 않기 때문에 저만의 추측을 해보았습니다.
제 생각은 만약 $f(x_t ⊙ (m ⊙ b))$만 해주게 된다면 단순히 $c_{y_t}$와 가깝도록 훈련될 수 있겠지만,
$c_{y_t}$와 feature가 완전 일치하게 m이 훈련될 수 있습니다.

즉, $x_t$가 어떤 feature 때문에 drifting sample인지에 대한 설명이 불가능해지고
단순히 $x_t$가 $c_{y_t}$와 같아지도록 훈련하는 게 되어버립니다.

저희가 원하는건 $x_t$가 $c_{y_t}$와 단순히 가까워지도록 훈련하는게 아닌
$x_t$가 $c_{y_t}$와 가까워지도록 하기 위해선 어떤 feature을 수정(마스킹)해야하는지 즉, sample x가 drifting sample 일때 가장 큰 기여를 한 feature을 찾아내는 것이 목표입니다.

그렇기때문에 $f(x_t ⊙ (m ⊙ b))$가 아닌 $f(x_t ⊙ (1 - m ⊙ b) + x_{y_t}^{(c)} ⊙ (m ⊙ b)))$을 통해서 i 번째 feature가 중요하다고 판단 될 땐 $\hat{z}_t$가 $x_{y_t}^{(c)}$로 상정되고 i 번째 feature가 중요하지 않다고 판단 될 땐 $\hat{z}_t$가 $x_t$로 상정됩니다.
즉, 전형적인 binary하게 훈련되는 수식입니다.

하지만, 위와 같이 상정되는데 한 가지 문제가 있습니다.
결국 $\hat{z}_t$은 $c_{y_t}$와 최대한 가깝도록 훈련되는데
$c_{y_t}$와 $x_{y_t}^{(c)}$은 매우 비슷하기 때문에 모든 feature에서 m이 1이 되도록만 훈련 될 가능성이 매우 높습니다.
이에 대한 보정을 하기 위해 본 논문에서는 세 번째 텀인 $R(m, b)$을 이용합니다.

세 번째 텀은 m이 1이 되는 개수를 최소화 하기 위한 역할을 합니다.

$R(m, b)$의 수식을 자세히 보시면 b는 learnable하지 않기때문에 저희 관심사가 아니며,
m에 대한 관점에서 바라보면 learnable한 m에 속한 변수에 0이 많을수록 $R(m, b)$의 값이 작아질 것이고 Loss 값이 최소화 될 것입니다. 반대로 learnable한 m에 속한 변수에 1이 많을수록 $R(m, b)$의 값이 커질 것이고 Loss 값이 매우 커질 것입니다.

m에 1의 개수를 최소화 하고 0의 개수를 최대화 하려는 이유는 important feature의 개수를 최소화 하기 위함입니다.
만약 important feature에 대한 제한이 없게 된다면 두 번째 텀에서 설명 했듯이
important feature의 개수가 많아지면서 어떤게 정말 중요한 important feature인지 알 수 없게 될 수 있기 때문입니다.

$\lambda$는 당연하게도 m이 0이 되는 개수를 최대화 하려는 로스값의 비중을 정하는 변수입니다.

네 번째 텀은 결합 분포임을 의미합니다.

$Q(p) = \prod_{i=1}^{q} p(m_i \mid p_i)$

$p(m_i \mid p_i)$는 i 번째 특성에 대한 마스킹 확률 $p_i$에 의해 i 번째 특성의 마스킹 여부인 $m_i$가 조건부로 결정이 된다는 의미이며 확률 분포를 따른다는 의미입니다. 이때 $m_i$는 Bernoulli distribution를 따르게 됩니다.

$\prod_{i=1}^{q}$는 이러한 확률분포 p를 결합 분포로써 정의하겠다는 의미입니다.
여기서 말하는 결합 분포는 단지 각 사건이 독립적으로 이루어진다 라는 의미입니다.
그렇기에 각 요소의 곱으로 표현됩니다.

위와 같은 의미를 갖는 $Q(p)$는 첫 번째 텀의 기대값을 구하는데 사용됩니다.
$m~Q(p)$는 결합 분포를 따르는 Q에 확률 분포 p를 입력했을 때의 m을 추출하겠다. 라는 의미입니다.

여기서 헷갈릴수 있는데 Q(p)의 수식을 보면 모든 $i$번째 요소들이 곱해져서 각 i 번째와 같은 특성이 없어진 상태에서 m이 추출되는게 아닌가? 라는 생각을 할 수 있습니다.

하지만 Q(p)에 있는 $\prod$는 단지 결합 분포라는 의미를 위해 사용된 수식이므로 그렇진 않습니다.

여기까지가 수식 (2)에 대한 설명이며 몇 가지 추가 정보들을 말해보겠습니다.
이제까지 제가 계속 m을 말할때 learnable하다고 말씀드렸습니다.
정확히 말하면 gradient-base로 훈련을 가정한다면 반은 맞고 반은 틀린말입니다.

그 이유는 m은 0 또는 1으로 continous variable이 아닌 discrete variable입니다.
이러한 discrete variable은 아쉽게도 gradient-base로 훈련이 불가능합니다.

그 이유는 gradient-base로 훈련이 되기 위해서는 훈련하고자 하는 variable이 continous해야 그 기울기를 구할수 있기 때문입니다.
하지만 discrete variable은 값이 continous 하지 않기때문에 기울기를 구할수 없습니다.

이를 해결하기 위해선 생각보다 간단합니다.
discrete variable을 continous하게 변환해주면 되며 그 방식을 본 논문에선 change-of-variable trick이라고 소개합니다.

조금 더 구체적으로 설명하자면 Bernoulli distribution (0과 1로 discrete하게 표현되는 분포)를 $p_i$에 의해 생성된 continous variable인 continous approximation으로 대체합니다.

그래서 두 번째 텀인 $f(x_t ⊙ (1 - m ⊙ b) + x_{y_t}^{(c)} ⊙ (m ⊙ b)))$에서의 이산 변수 $m$을 확률 변수 $\hat{m}$으로 변경한다고 생각해주시면 될 것 같습니다.

이렇게 되면 $m$은 이산 변수가 아닌 확률 변수로써 continous variable이 되면서 gradient-based training이 가능해지며 adam으로 훈련이 가능해지게 됩니다.

3. Experiments

Dataset

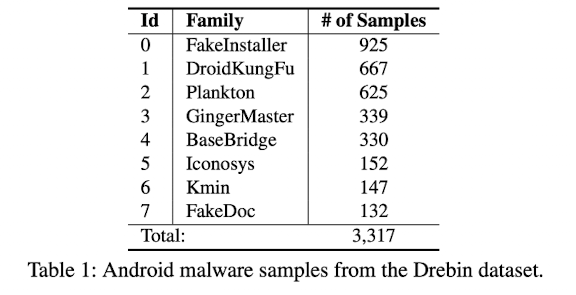
본 논문에서는 총 8개의 family를 최소 100개 이상의 data를 갖도록 세팅해주었습니다.
특히 drifting sample을 탐지하기 위해 총 8개의 family 중 하나의 unseen family를 설정해줍니다.

예를들어 unseen family를 FakeDoc으로 설정하면 FakeDoc을 제외한 family에 대해서만 훈련을 해줍니다.
그리고 drifting sample을 탐지하기 위한 test 단계일 때 FakeDoc을 입력해줍니다.

그리고 unseen family로 설정 되지 않은 나머지 family에 대해선 training dataset과 testing dataset을 8:2의 비율로 나눠줍니다.

Feature Remove

본 논문에선 CICIDS 2018 dataset과 Drebin dataset을 사용합니다.
Drebin dataset에는 총 7,218개의 feature가 존재하는데 매우 고차원이기 때문에 이런 경우 training시에 잘 안될수 있습니다.

feature의 고차원인 부분을 저차원으로 일차적으로 줄여주기 위해 본 논문에서는 간단하게 scikit-learn's VarianceThreshold function을 이용하여 1,340개의 feature까지 줄여줬습니다.

Various Cases in Latent Space

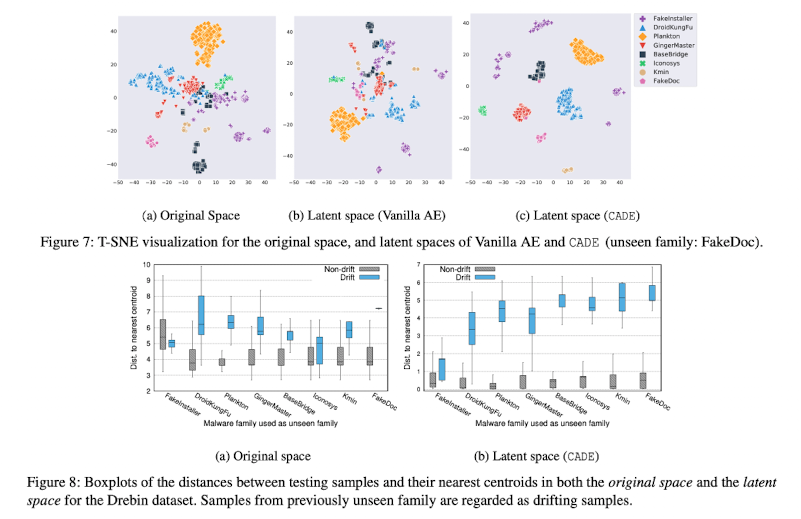
Introduction에서 말했듯이 Figure 7을 보면 Latent space에서 CADE 방식이 가장 Contrastive하게 각 각의 클래스가 나눠져 있는 것을 볼 수 있습니다.

또한 Figure 8을 보면 Original space에서는 Non-drift sample과 Drift sample의 거리 편차가 크게 나지 않았습니다.
특히 FakeInstaller, Iconosys에서는 거의 차이가 없는 것을 볼 수 있습니다.

그에반해 CADE에서는 어느정도 확연한 차이를 볼 수 있습니다.

Evaluation of Drifting Sample Detection

위 테이블에서는 drifting sample에 대한 F1 score을 보여줍니다.
CADE 방식에서 F1 score가 가장 높게 나오고 비교 method와는 확연한 차이를 보이고 있습니다.

Case Study: Limits of CADE

대부분의 경우에서 CADE는 잘 작동합니다. 하지만 특정한 경우에선 잘 작동하지 않습니다.
예를들어 가장 많은 data amount를 갖는 Fake-Installer를 unseen family로 정한다면, recall score은 100%를 갖는데에 비해 precision은 82% 밖에 갖지 못합니다.

GingerMaster, Plankton families에서 특히 이와 같은 현상이 많이 발생합니다. 해당 familes에서 precision이 낮게 나오는 이유에는 크게 두가지가 있습니다.

• training dataset과 testing dataset을 8:2로 나누는 상황에서 GingerMaster, Plankton data는 그 양이 적습니다.
  이에 따라 latent space에서 정확한 clustering가 형성되지 못합니다.
• GingerMaster, Plankton families는 기본적으로 많은 변형이 있는 data입니다. 즉 같은 label을 갖는 family이지만 변형에 따라 다른 분포로 표현이 될 가능성이 높은 data입니다.

Evaluation of Explaining Drifting Samples

제 개인적인 생각으로는 CADE의 꽃은 Drifting sample detection보단 Drtifting sample을 Explaining하는 기법이라고 생각합니다.

CADE가 Drifting sample을 얼마나 잘 Explaining 하는지 확인하기 위해 perturbed feature한 sample이 얼마나 nearest centroid에 가까워졌는지 확인하기 위한 수식은 아래와 같습니다.

$d'_{x_t} = \| f(x_t \odot (1-m_t) + x_{y_t}^{(c)} \odot m_t) - c_{y_t}\|_2$

• $d'_{x_t}$는 perturbed feature한 sample과 nearest centroid의 거리를 나타냅니다.
• $x_t$는 origin sample을 의미합니다.
• $x_{y_t}^{(c)}$은 nearest centroid에 가장 가까운 sample을 의미합니다.
• $(m_t)_i$는 i번 째 feature의 mask를 의미합니다.
  만약 $(m_t)_i$ = 1이라면, i번 째 feature가 중요하다고 판단 된 것이고 수식에 의해 $x_t$대신 $x_{y_t}^{(c)}$의 feature로 대체될 것입니다.
  만약 $(m_t)_i$ = 0이라면, i번 째 feature가 중요하지 않다고 판단 된 것이고 수식에 의해 $x_t$의 feature 그대로 사용될 것입니다.

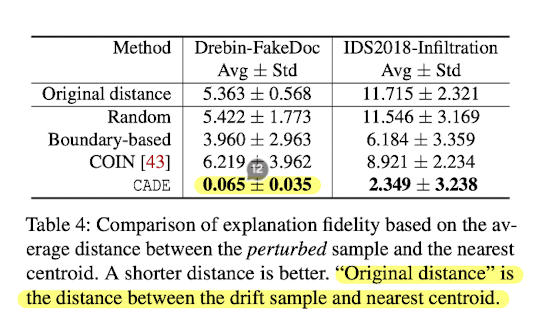
위 이미지는 위 수식에 따라 각 Method에 따른 Distance를 나타냅니다.
특히 Method인 Boundary-based보다 월등히 높은 거리 차이를 보이고있습니다.

즉, 위 수식을 통해 important feature을 도출해내고 그 feature을 적용했을 때의 기법인 CADE가 boundary-based 기법보다 더 효과적입니다.

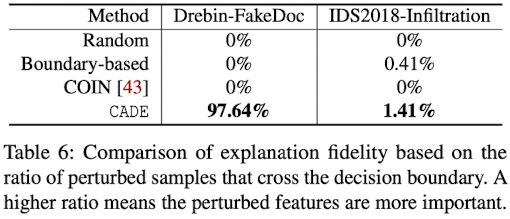
위 이미지도 같은 맥락인데, 마찬가지로 각 Method에 따른 decision boundary 안으로 들어갔는지 안들어갔는지에 대한 비율입니다.

CADE는 decision-boundary 방식이 아니기에 굳이 이런 방식을 사용할 필요는 없지만,
다른 Method에 비해 경쟁력 있다는 것을 어필하기 위해 비교한 것으로 보입니다.

예를들어 CADE Method를 이용하여 Drebin의 FakeDoc family인 drifting sample을 decision-bondary 안으로 성공적으로 들어가게 했는지를 확인합니다.

위 이미지를 보시면 아시겠지만 CADE method일 때 97.64% 비율로 decision-boundary 안으로 들어간 것을 보실 수 있습니다.
오히려 정작 decision-boundary 방식인 Boundary-based에서는 0% 비율로 decision-boundary 안으로 들어간 것을 보실 수 있습니다.

이를 통해 알수 있는 사실은 boundary 방식이 아닌 distance 기반으로 important feature을 찾아내는 방식인 CADE의 explanation이 더 효과적인 것을 확인할 수 있습니다.

본 논문에서는 drifting sample이 nearest centroid와 얼마나 거리적으로 가까운지 뿐만 아니라
위와 같이 drifting sample을 실제로 잘 explanation 하고 있는지에 대해 나타냅니다.

우선, 위 이미지에 나오는 feature들은 $(m_t)_i$ = 1 즉, important feature이라고 선언된 feature들을 나타냅니다.
또한 drifting sample는 FakeDoc일 때, closet family는 GingerMaster인 상황입니다.

실제 FakeDoc Malware은 보통 희생자가 SMS를 통해 프리미엄 서비스에 가입하도록 하는 악성 프로그램입니다.
다시 말해서 SMS 및 결제 권한과 관련이 많은 Malware 프로그램입니다.

실제 위 이미지에서도 GingerMaster와 unseen family이자 drifting sample인 FakeDoc을 구분하는 가장 큰 feature로써 SMS 관련 권한이 많은 것을 볼 수 있습니다.

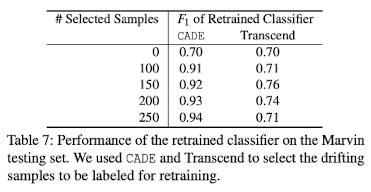
위 Table은 unseen family일 때를 가정 한 것이 아니라 existing class인 경우를 가정한 것입니다.

예들들어 FakeDoc을 unseen family로 가정한 경우였다면 training때 FakeDoc을 훈련하지 않습니다.
즉, training때 FakeDoc을 훈련하지 않았기 때문에 testing 상황에서 FakeDoc은 unseen family로 분류되는 것입니다.

existing class인 경우는 예를들어, FakeDoc을 training때 같이 훈련합니다.
그리고 나서 testing 때 FakeDoc을 제대로 FakeDoc이라고 판단하는지 확인합니다.

existing class인 경우 그 탐지가 쉬울 것 같지만 본 논문에서는 시간이라는 조건을 추가됐다고 봐주시면 됩니다.
2010년에 등장한 FakeDoc과 2014년에 등장한 FakeDoc은 높은 확률로 그 Distribution이 다를 것입니다.

그 이유는 공격자 입장에서 섬세하고 정교하게 FakeDoc 공격을 성공하기 위해 그 정보를 조작할 것이기 때문입니다.

그래서 본 논문에서는 기존에 사용했던 Drebin dataset 뿐만 아니라 Marvin dataset도 사용하였습니다.
Drebin은 2010-2012년 까지의 dataset이고 Marvin dataset은 2010-2014년 까지의 dataset입니다.

그 결과 Marvin dataset에 대해서 F1 score가 70%로 매우 낮게 나왔습니다.
그 뒤, CADE Method를 통해 Marvin dataset의 drifting sample들을 찾은 다음 100~250개 사이의 drifting sample을 기존의 dataset에 추가한다음 retraining 한 결과 91~94%까지 F1 score의 향상이 이루어졌습니다.

4. 후기

생각보다 수식 (2)가 이해하기 어려워서 정리하는데에 많은 에로사항과 시간이 걸렸습니다.
그럼에도 불구하고 CADE 논문은 concept drift와 CL을 이용한 XAI 방법론에 대해 매우 질 높은 논문이라고 생각하여 꼭 한 번은 정리하고 싶었습니다.

확실히 찝찝하게 끝내는것보다 이런 논문은 기간이 좀 걸리더라도 확실하게 끝내는게 마음이 편한것 같습니다.

읽어주셔서 감사합니다.