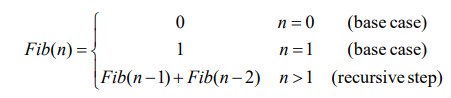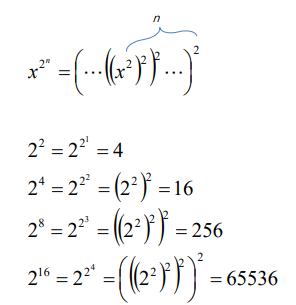알고리즘 - 2(재귀)

재귀

---

Recursion

• 어떤 함수에서 직,간접적으로 자기 자신 함수를 다시 호출 하는 것
• base case : 직접 함수값을 계한할 수 있는 경우, 1개 이상 필요
• recursive step : base case가 만들어 질 떄까지 자신을 재귀 호출해 나가면서 계산하는 과정

---

Type of recursion

• 재귀가 호출되는 부분(횟수 말고 한번에 몇번 호출 되는지)에 따라 구분
  • Unary recursion
    • factorial, linear sum
  • Binary recursion
    • fibonacci, hanoi tower
  • Multiple recursion
    • flood fill, knight tour

---

Factorial

• 
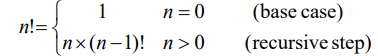
• 반복문으로도 가능은 한 케이스

---

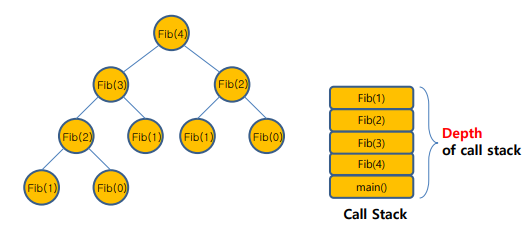
call stack

• 함수를 새로 호출할때 기존에 실행중인 함수의 지역변수 같은 정보를 저장하기 위해 필요
• 현재 함수가 가지고 있던 정보를 저장하는 메모리 공간이 activation record이고 이를 call stack에 저장함
• call stack은 제한적이기 때문에 재귀의 횟수가 너무 크면 call stack overflow가 일어남

---

Fibonacci

• 
• 

---

Linear Sum

• 배열의 특정 인덱스까지의 합
• 
• 

---

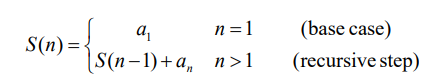
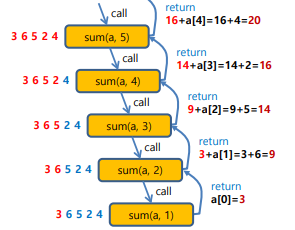
Reversing Array

• 배열 특정 구간을 앞뒤로 뒤집기
• 맨 앞, 뒤를 swap하고 앞은 +1 뒤는 -1하는 방식
• 
• 여기서의 base case는 i가 j와 겹치거나 커지는 경우인데 swap할 필요가 없어서 코드에 안 적어도 됨

---

Computing Powers(거듭제곱)

• 
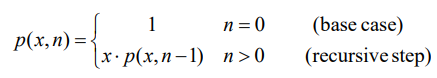
• x를 곱해야 하는 수를 1씩 줄임
• 숫자가 높으면 한계가 있음

Fast Computing Powers

• double squaring
  • 
• 
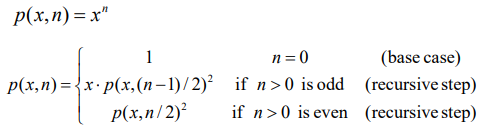
• x^8은 x^4의 제곱, x^4는 x^2의 제곱

---

최대 공약수

• 유클리드 호제법
  • 
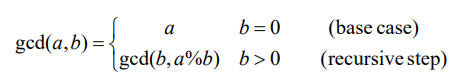
  • a%b = r일때 a,b의 최대공약수는 b와 r의 최대 공약수와 같다
  • a,b를 나누고 b를 a로 나머지를 b로 보냄
  • 나누어 떨어질때 : b가 0일때의 a가 최대 공약수(여기서 a,b의 구분이 중요)

---

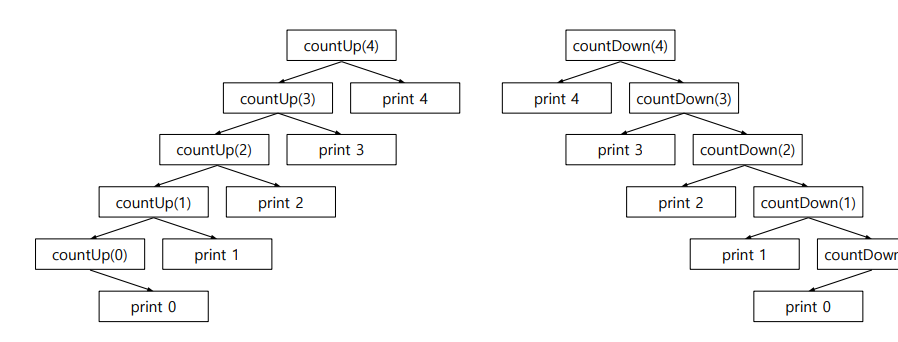
Count Up / Count Down

• 
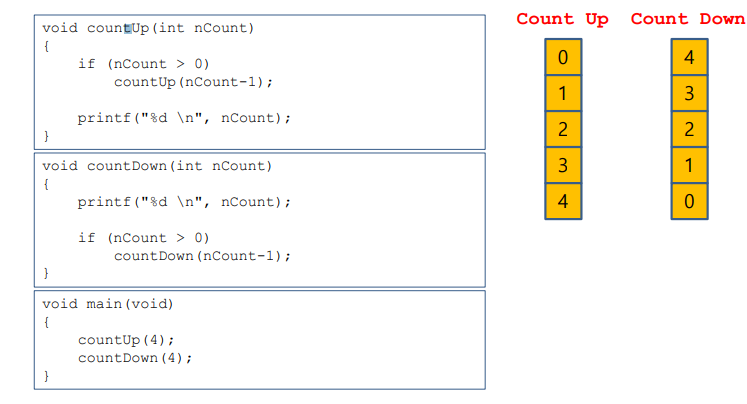
• 함수의 호출과 print명령어의 순서 차이
• 

---

팰린드롬 검사(회문)

• 
• 맨 앞과 맨 뒤를 검사(다르면 종료(회문이 아님)
• 맨 앞과 맨 뒤를 한칸 씩 당겨온 뒤 재검사
• 맨 앞과 맨 뒤의 인덱스가 같거나 맨 앞의 인덱스가 더 커지면 종료(회문)

---

십진수 진수 변환

• basetable : 진수의 크기 만큼 사용하는 문자
• 
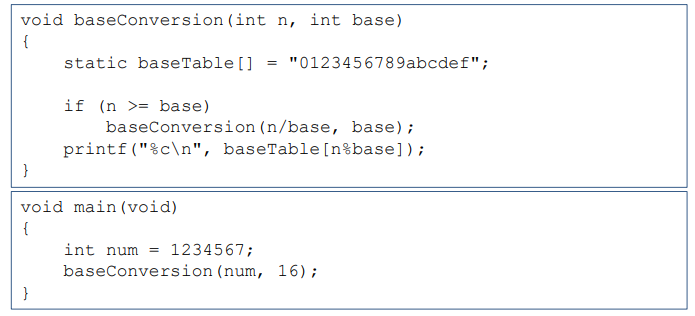
• 각 재귀에서 진수의 크기만큼 나눈 몫을 인자로 넘기고 나머지는 출력
  • 몫이 진수 한칸에 포함하는 최대 값이고 나머지는 그 다음 자리로 넘겨야함

---

permutation(순열)

• 순열의 개수
  • n개의 문자로 만든 순열의 수 : n!

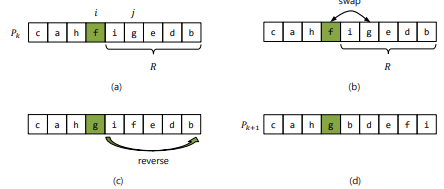
나라야나 판디타 알고리즘

• 주어진 순열의 다음 순열 계산 알고리즘

1. 순열의 마지막에서 시작해서 역순으로 오른차순을 만족하는 최대 구간 R을 찾음
2. R의 길이가 최대 길이인 경우 마지막 순열인 경우임
3. R의 길이의 의미 : R만큼의 개수로 만들수 있는 순열의 마지막 순열
4. R하나 앞의 인덱스에 해당하는 값보다는 크면서 R중에서는 가장 작은 값을 찾음
5. 두개를 교환(R의 앞까지의 순열을 바로 다음 순열로 바꾸는 과정)
6. R을 뒤짐음(R은 그 길이의 순열 중 최대값이므로 뒤집으면 최소가 됨)

• 

---

permutation 만들기(recursive)

• 순열의 길이를 1씩 줄여가면서 순열을 계속 만드는 방식
• 
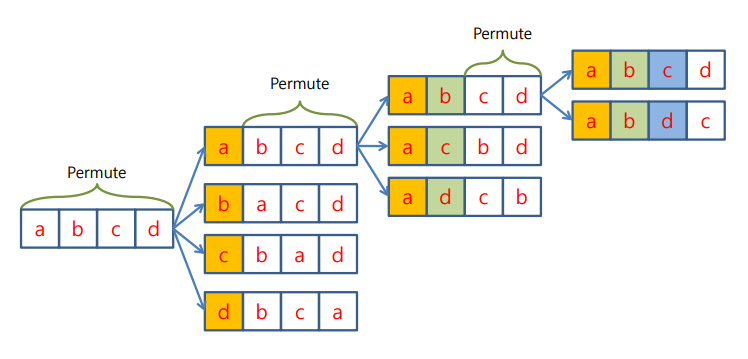
• 순열의 처음 길이 만큼 for문 사용
  • 처음 단어로 시작하는데 i만큼 떨어진 단어를 swap해서 모든 문자가 처음 시작할 수 있게 해줌

  ---

  Hanoi Tower

• 
• 
• 
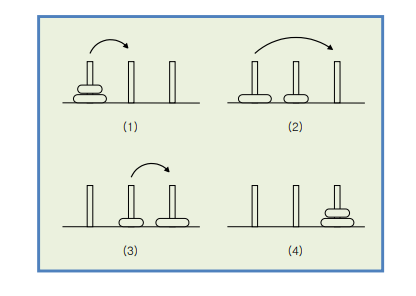
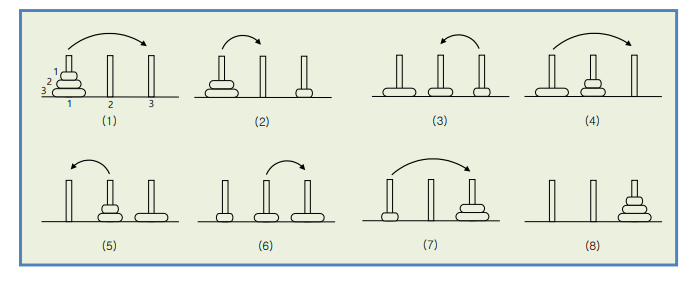
• n-1개를 1에서2로 옮기로(재귀) 제일 큰걸 1에서 3으로 옮기고(실질적 움직임) 옮겨놨던 n-1개를 2에서 3으로 옮김(재귀)
  • 
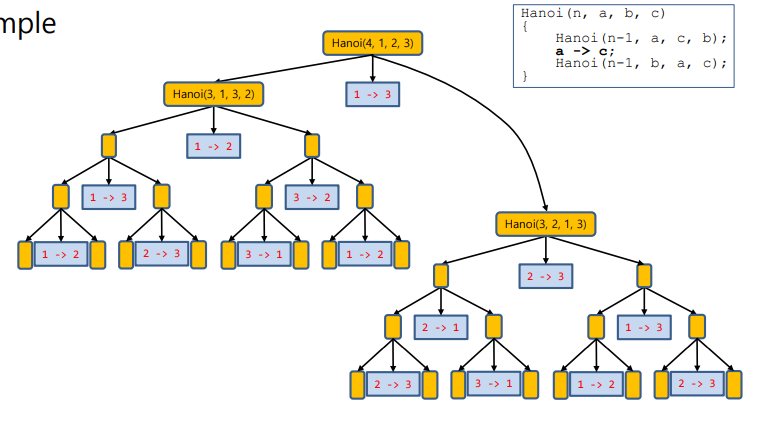
  • 재귀 함수의 인자 3개중에 가운데를 안쓰는 봉으로 생각 가운데, 오른쪽, 왼쪽을 안쓰는 순서로 재귀
    • 
• 계산 횟수
  • 
  • 2^n - 1

---

Knight Tour

나이트가 64개의 모든 체스판을 중복없이 방문하도록하는 경우의 수

• 모든 판을 방문 후 한번 더 이동하면 원래의 위치로 이동하는 케이스와 상관없는 케이스가 있음
• 움직일 수 있는 위치 8개 설정, 지나간 곳인지 마크할 2차원 배열 설정, 몇번쨰로 방문한 곳인지 표시할 2차원 배열 설정
• 
• 이동할 수 있는 방향 8곳으로 재귀함수를 돌림
  • 이동할 곳이 마크가 없거나 체스판의 밖이 아닐 경우에만 이동
  • 

---

Binary Tree

• base case를 empty 노드로 정의

• 

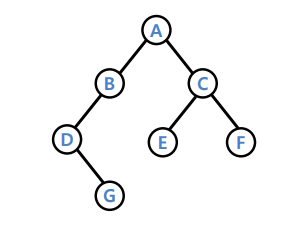
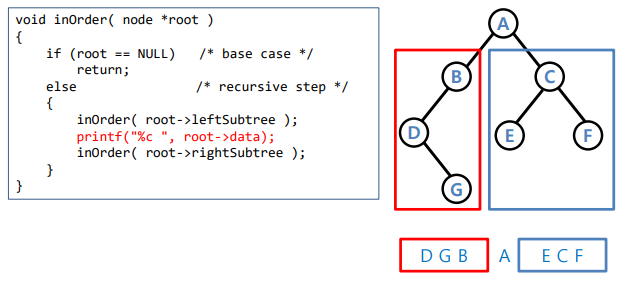
• In-Order

  • 왼쪽, 루트, 오른쪽 순서
    • 
  • root =- NULL 서브트리가 없으면 리턴하기 위함

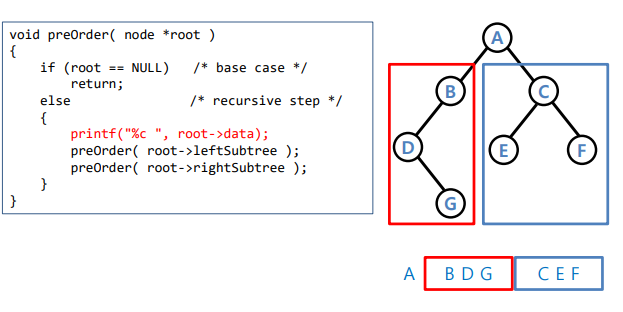
• Pre-Order

  • 루트, 왼쪽, 오른쪽 순서
    • 

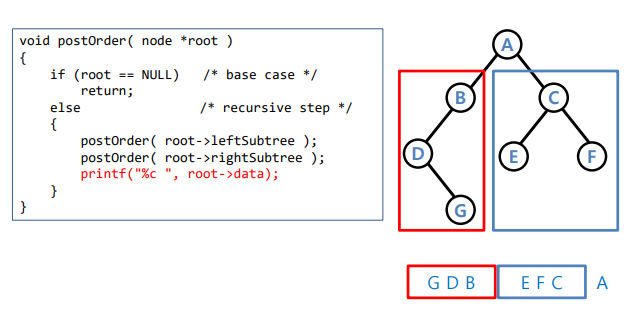
• PostOrder

  • 왼쪽, 오른쪽, 루트 순서
    • 

• Tree Traversal

  • 
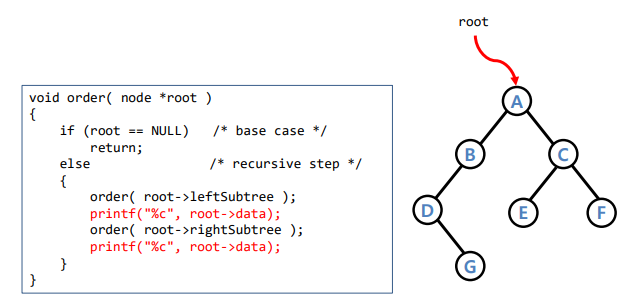
  • D G G D B B A E E C F F C A
  • 왼쪽,루트,오른쪽,루트의 순서

• 노드의 개수 측정

  • int size( *root)
    {
     if(root == NULL)
     	return 0;
     return size(root -> leftsub) + size(rightsub) + 1
     }

  • 루트의 개수만 하나씩 세고 null일떄는 개수에 포함 안시키고 리턴
    

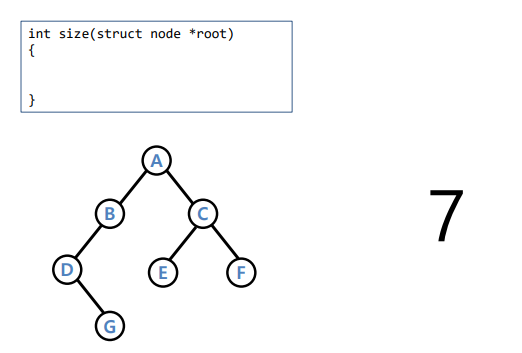
• height

  • int height(* root)
    {
     if(root == NULL)
     	return -1
     return max(height(root -> left), height(root -> right)) + 1

  • 리턴 하면서 올라갈때 +1, 왼 오 중 max값을 사용
  • 

---

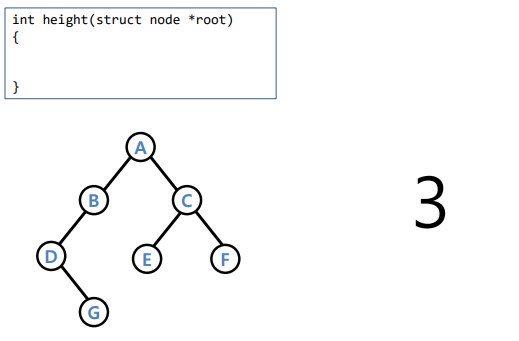
코드 짜봐야 하는거

• mirror

• insert
• destruct

---

• sumofweight
  • 
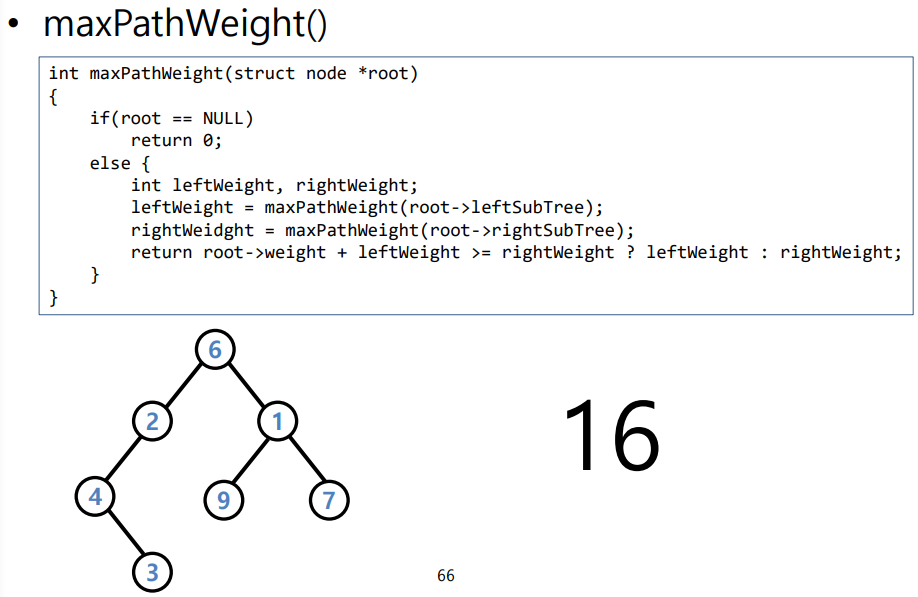
• maxPathWeight
  • 

---