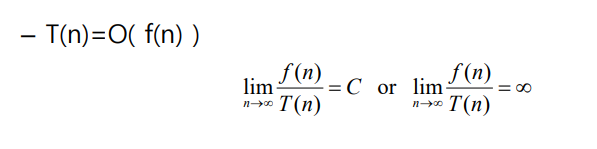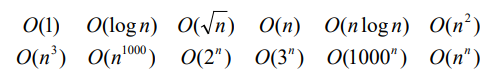알고리즘 - 3(분석)

알고리즘 분석

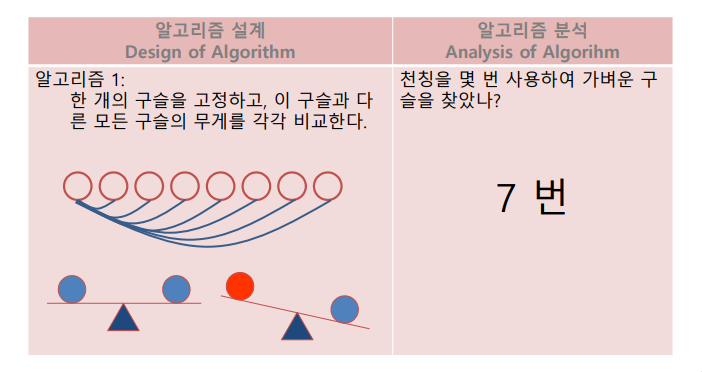
• 무게가 가벼운 구슬 찾기
  • 8개의 구슬 중 가벼운 구슬 1개를 천칭을 이용해서 찾는 방법
    • 
    • 
    • n/2으로 recursive하게 나눠서 계산(log2(n))
    • n/3으로 나누는 방법도 있음(log3(n))
      • 3개의 그룹으로 나누면 2개는 천칭으로 비교하고 나머지 그룹 1개는 자연적으로 계산 가능

---

• 알고리즘 비교
  • 
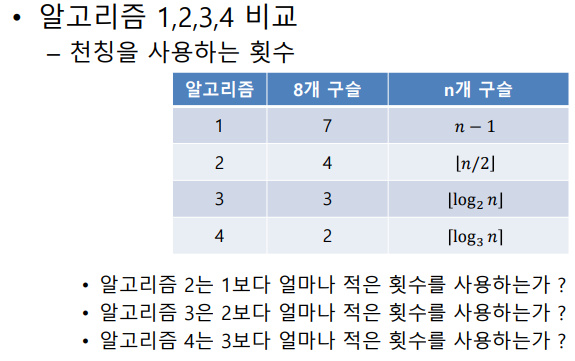
  • 1,2 비교
    • 
    • 
  • 3,4비교
    • 
    • 
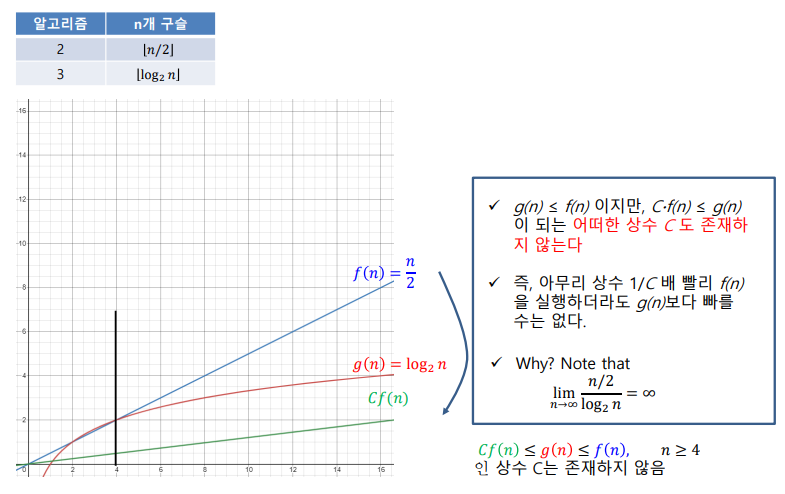
• 1,2와 3,4는 상수로 효율을 표현해서 매우 큰 의미가 없지만 2,3의 비교는 상수의 배수로 표현이 불가능함 이 2개의 비교가 실질적으로 의미있는 차이임
  • 

알고리즘 간의 차이가 상수배로 표현 가능하면 하드웨어에 따라 역전 가능하기 떄문에 알고리즘적으로는 의미가 없다는 뜻

• 
• 
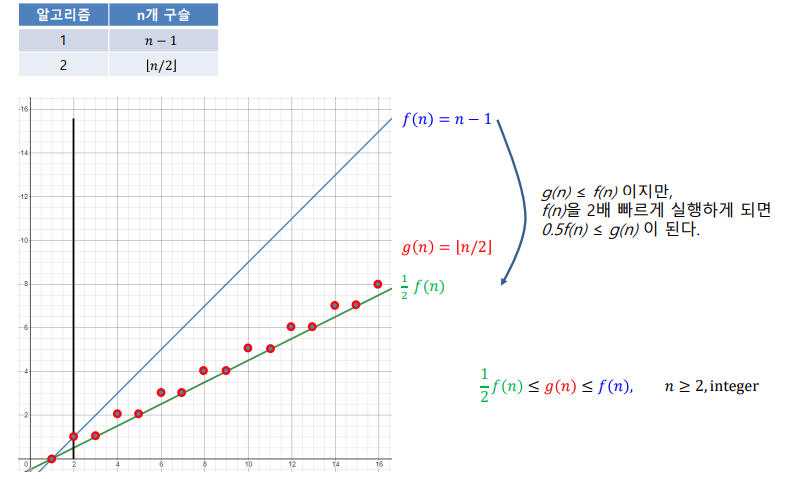
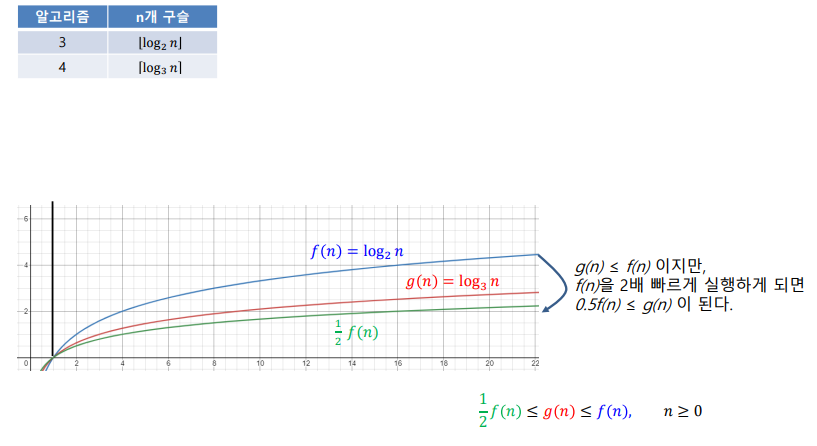
• 알고리즘 간의 차이가 의미가 있는 경우
  • 

---

시간, 공간 복잡도

• 
• 시간 복잡도
  • Basic Operation
    • 알고리즘의 수행시간이 어떤 연산의 수행 횟수에 비례하는 핵심적인 연산을 찾아서 그 연산이 수행되는 회수를 계산
  • primitive operation
    • 모든 assignment, array indexing, 덧셈, 곱셈, 함수호출 회수를 계산

---

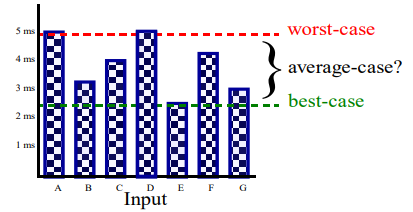
• 수행시간은 입력되는 데이터의 종류에 따라 다르지만 worst-case를 기본으로 하고 가끔 average-case도 고려
  • 
• Basic, primitive의 차이(Basic을 사용하는 이유)
  • 결국 두 개의 차이는 상수배만큼의 차이로 나타나기 떄문에 복잡하게 primitive를 사용할 이유가 없음
  • 

---

Big O Notation

• 버블정렬의 시간 복잡도 n(n-1)과 선택정렬 n(n-1)/2은 약 2배정도의 차이가 있는데 이는 소프트웨어, 하드웨어 환경에 따라 뒤집힐 수 있으며 알고리즘적으로는 의미가 없다
• 극한을 도입해서 비교(n이 무한대로 갈 경우)
  • 
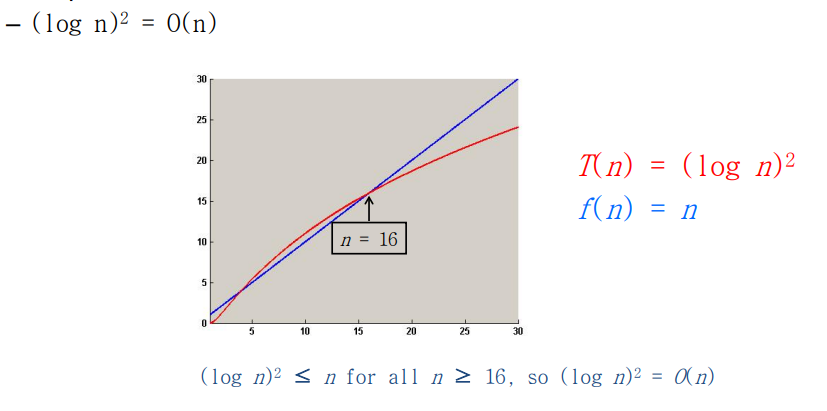
• Big O Notation에서는 상수와 차수가 낮은 부분은 제외하고 최고차수로만 표기
  • ex) 3n^2 + 5n이면 O(n^2)
• 
• 특정 구간 이후에서 모든 n에 대하여 O(n)보다 작으면 O(n)으로 표기 가능 즉 조건을 만족하는 식중 가장 작은 식을 대입하는 것이 좋음
  • 
  • 
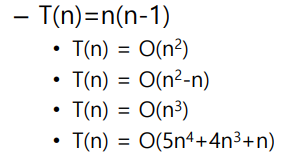
  • 극한으로 대입하면 상수배로 나눠지거나 함수가 분모일떄 무한대가 되면 됨
    • 
• 정리 : 가장 고차단항을 계수가 1인 식으로 표현
  • 
• 순서
  • 

---

Analysis of Algorithms : Example

MCSS

• n개의 정수가 주어졌을때 연속적인 부분수열의 합이 최대가 되는 구간과 그 구간의 합을 계산

• ex)

  • 

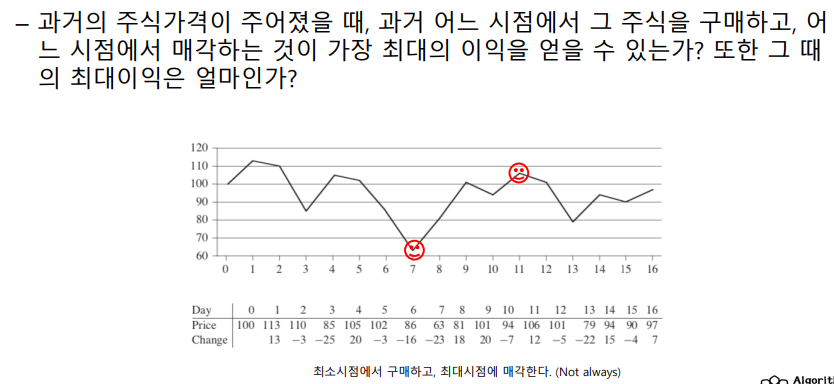
• 최소시점 구매, 최대시점 매각

• 방법 1

  • 
  • 모든 구간의 합을 계산하고 그 중 가장큰 값을 계산
  • O(n^3)

• 방법 2

  • 
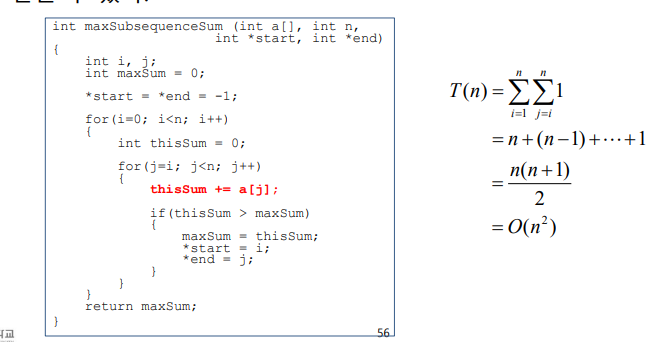
  • 방법 1에서 시작 위치는 같을때 구간의 길이가 1늘어나면 이전 값에 새로운 인덱스값 하나만 더하는 방법
  • O(n^2)

• 방법 3(Kadane's Linear Algorithm)

  • 
  • 현재 구간에 새로운 인덱스를 더해서 양수가 되면 그 다음 인덱스로 넘어가고 음수가 되면 리턴하고 그 다음 인덱스부터 새로 구간을 만들기 시작하는 방법
    • 더했을때 양수가되면 바로 다음 수까지 구간을 늘렸을떄 이전 구간을 붙이는게 이득이기떄문

---