Greedy Approach
- 일반적으로 여러개의 원소 집합에서 부분집합이 해답일때 부분집합을 구할때 사용함
- 해답을 집합 g라할때 처음엔 공집합, 주어진 원소에서 g에 포함될 원소를 차례로 1개씩 선택
- 원소 선택과정에서 전후 관계를 고려하지 않음
동전교환
- 1,5,10,50,100으로 378원을 교환해주기

- 동전교환에서는 값이 큰 동전부터 선택
- 문제점

- 일반적인 경우는 DP로 품
가방 채우기
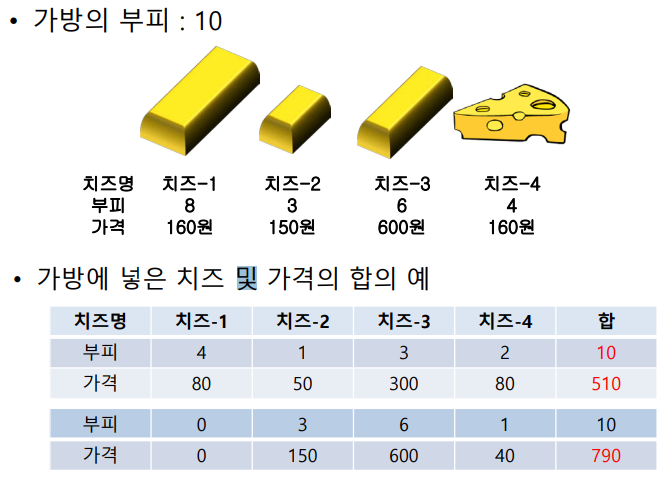
- 단위 부피당 가격이 높은 치즈부터 채움
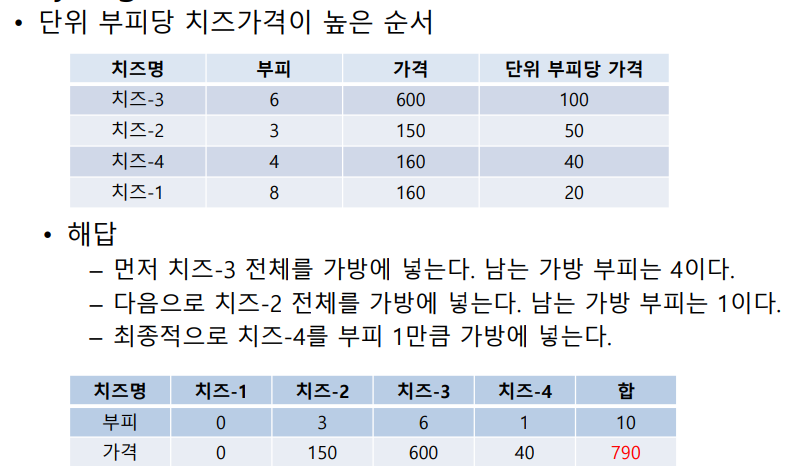
- 치즈를 자를 수 없는 경우는?
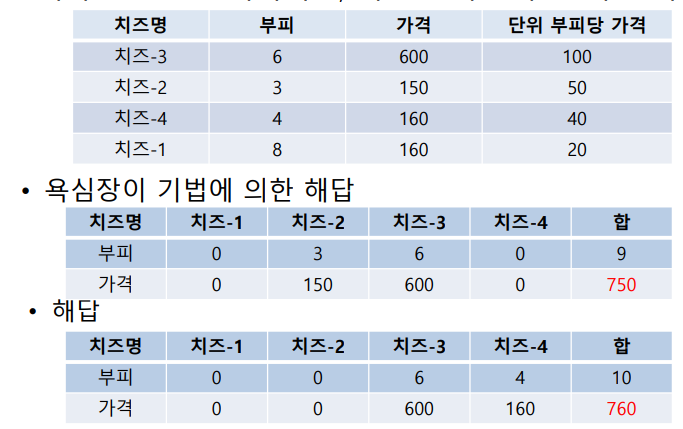
- 이 경우에는 DP로 풀어야 함
회의실 배정 문제

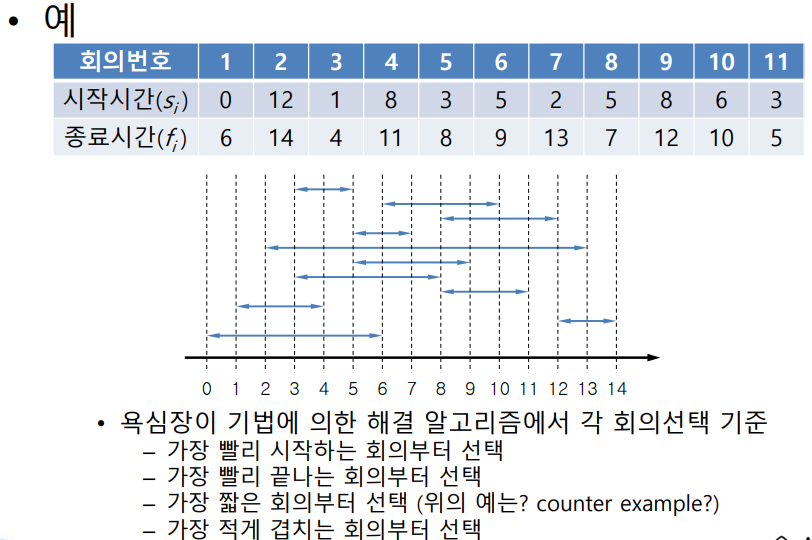
- 가장 빨리 끝나는 회의부터 선택

- 이때 그 다음 회의를 고를때는 시작시간이 이전 회의의 종료시간보다는 커야함
Minimum Spanning Trees
- 모든 V를 포함하면서 connected인 트리
- 그중 웨이트의 합이 가장 작은것을 구하는 것임
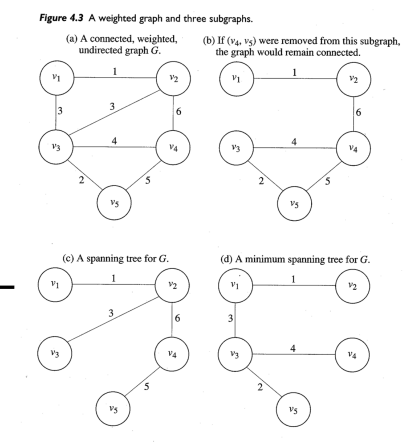
- 1,2는 사이클이 있기 떄문에 트리가 아님
- 3,4둘다 spanning tree인데 웨이트가 더 작은 4가 minimum spanning tree
- Prim, Kruskal 2개의 알고리즘이 있음
Kruskal`s algorithm
MST를 찾는것
- 웨이트가 작은 엣지순서로 정렬
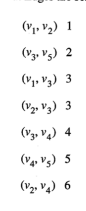
- 웨이트가 작은 엣지부터 추가함
- 엣지를 추가해서 사이클이 생기면 추가 안함
- v가 5개면 엣지 4개를 구하면 종료임
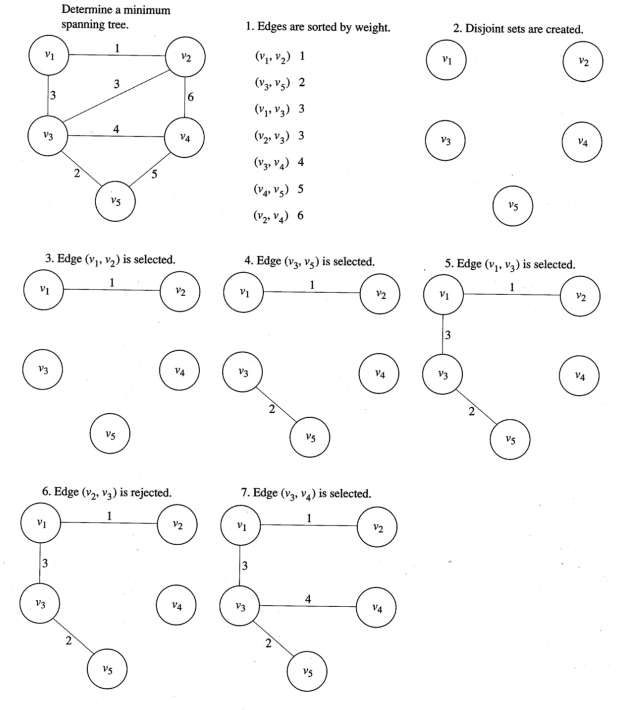
- 엣지를 추가할때마다 사이클이 만들어지는데 검사하는게 중요
- 이걸 유니온 파인드로 검사함
- 새로 추가할 엣지에 연결될 P와Q가 유니온 파인드의 같은 트리에 속하면 사이클이 생김, 다를떄만 엣지를 추가하고 UF에서 merge함
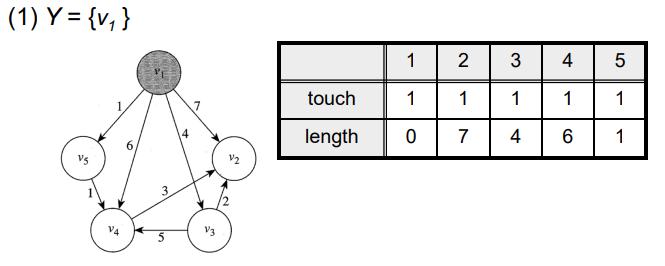
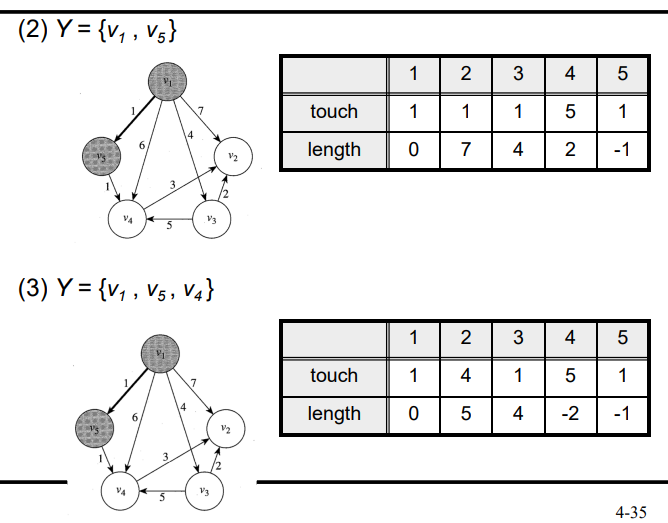
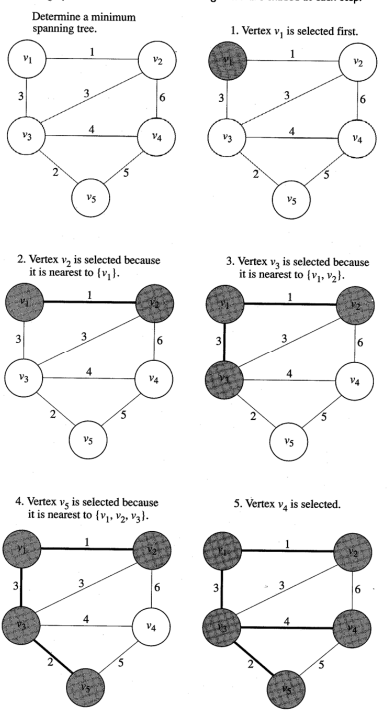
Prim`s Algorithm
- 한 버텍스에서 시작(크루스칼)은 엣지를 추가하는 방식
- 전체 버텍스를 y라함
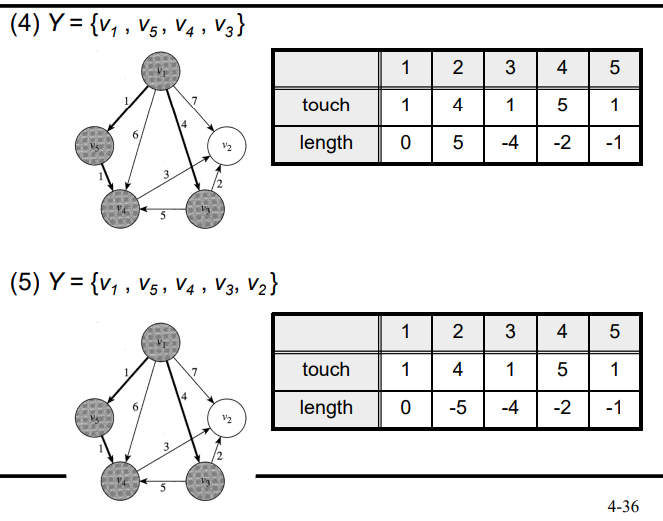
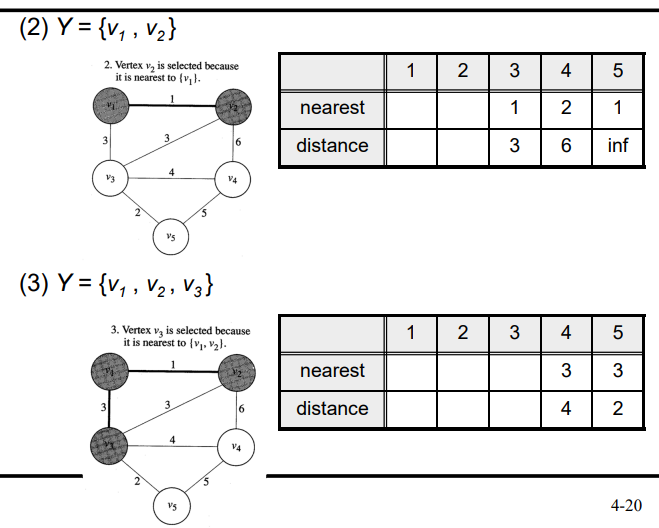
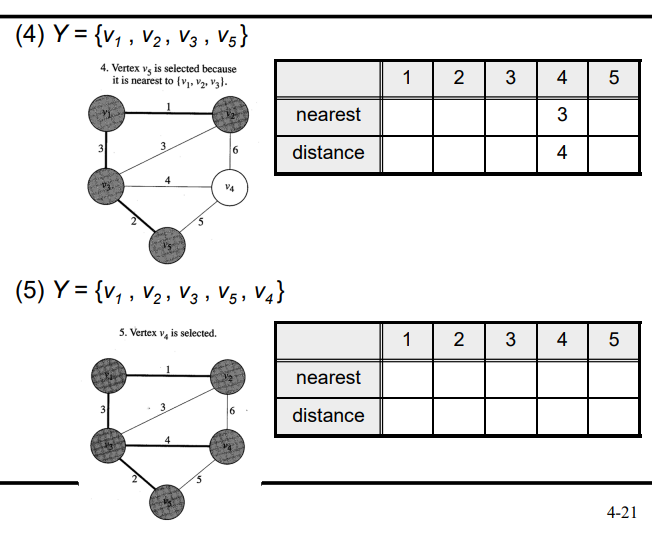
- V를 하나 고르고 V와 y-v를 잇는 엣지 중 가장 웨이트가 작은 엣지를 고르고 이은 버텍스를 V에 추가
- 위 과정을 반복
- 엣지를 선택할때 최소값만 사용하기 때문에 각각의 V는 자신과 이어준 엣지중 가장 웨이트가 작은 엣지만 관리하면 됨
- V를 추가하면서 V에 연결된 노드도 갱신 연결된 노드는 nearest, 거리를 distance로 관리함
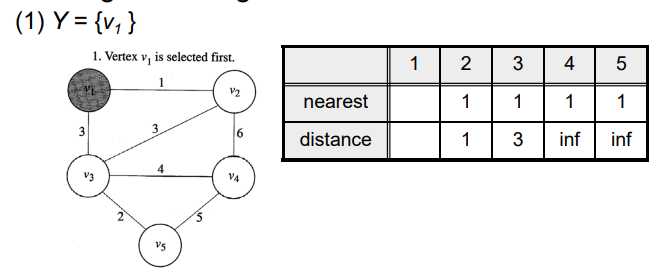
- 여기서 거리가 무한대여도 제일 가까운 노드를 1로 초기화 하는게 중요
Dijkstra`s Algorithm
- 가장 짧은거 고르고, 추가된 곳을 경유해서 가는게 더 빠르면 그 값으로 갱신, 가장 짧은거 고르기 반복