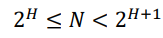Computational Complexity
- 문제 자체를 분석하는 분야
- 문제가 컴퓨터로 해결 가능한가?
- 문제의 lower bound가 몇인지
- lower bound : 문제 해결의 최고 효율(더 좋아질 수 없음)
Heapsort
- Priority Queue사용
- Binary Tree를 사용함
- Complete Binary Tree
- 제일 밑 레벨을 제외한 레벨에서는 모든 노드가 차있고(리프 2개) 제일 밑 레벨은 맨 뒤에서부터만 연속적으로 없어도 되는 구조
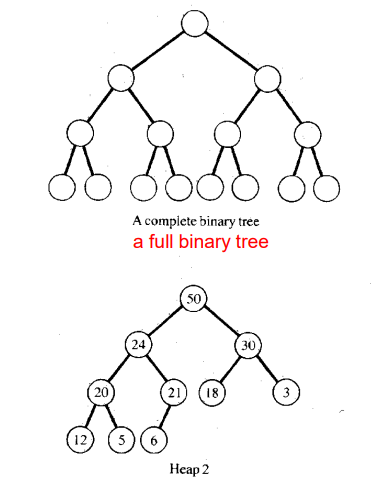
- Complete Binary Tree
- BST는 1차원 배열로 표현 가능
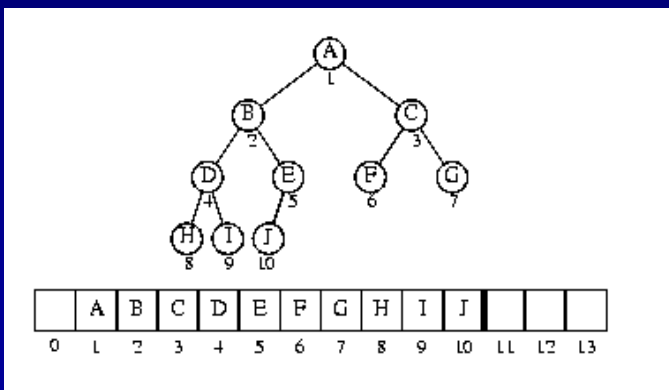
- 왼쪽 리프인덱스는 x2, 오른쪽은 x2+1(루트 인덱스가 1일떄)
- 리프에서 부모노드의 인덱스는 2로 나누고 버리면 됨

- 특성
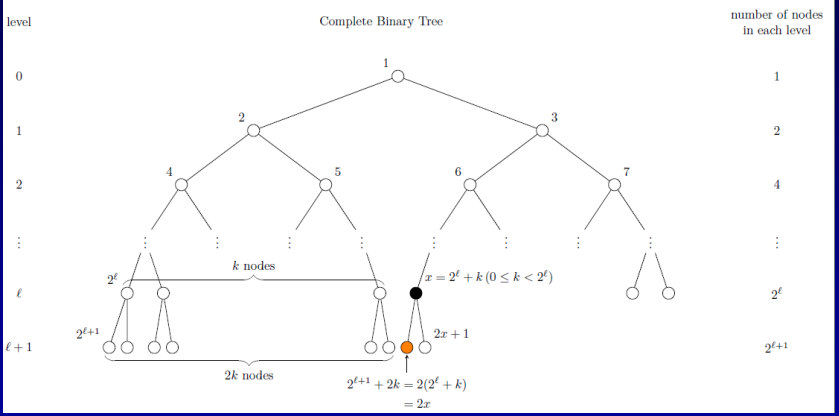
- 한 레벨의 노드의 개수는 2^L개
- Height는 max level
- full binary tree에서 노드의 개수는 2^h + 1
- complete binary tree에서는
- n개의 노드가 있는 complete binary tree의 H는
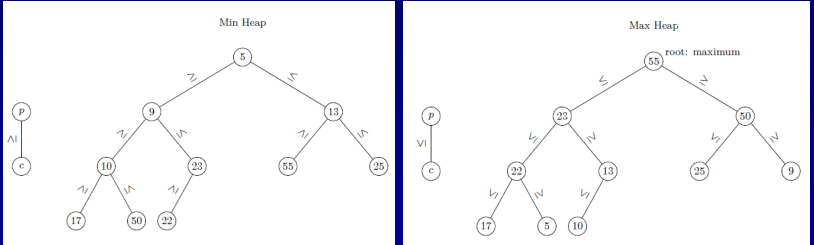
- parent가 크면 Max Heap 작으면 Min Heap(이 둘중 하나를 만족해야 Heap임)
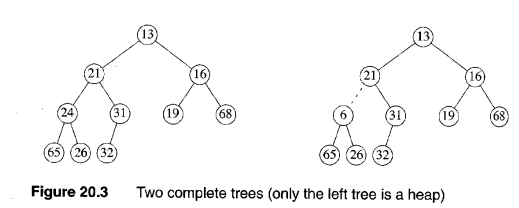
- 왼쪽만 Heap(둘다 complete tree이긴함)
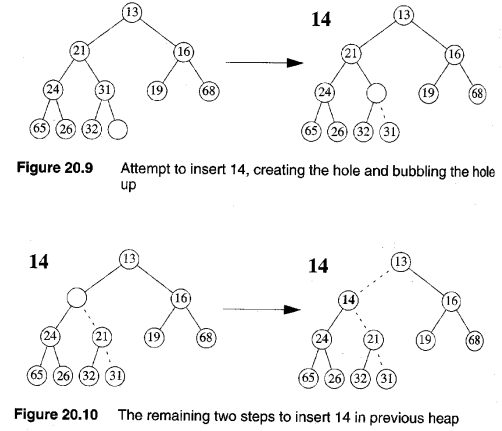
- Insert
- 일단 트리의 특성을 유지하기 위해 제일 밑에 추가함
- 그 후에 추가한 노드를 Heap의 특성을 유지하기 위한 알맞은 위치로 옮겨줌
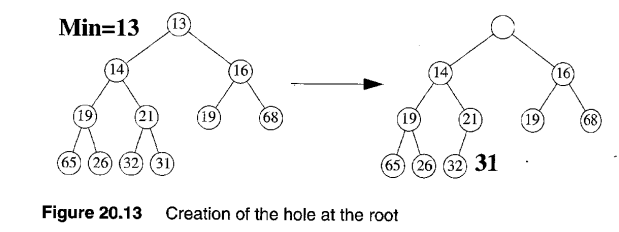
- Delete
- 먼저 삭제하고 싶은 노드를 삭제함(min, max인 루트 노드만 삭제 가능)
- 제일 밑의 오른쪽을 삭제한 위치(루트)로 옮김(complete binary 트리의 성질을 유지하기 위해 제일 밑의 오른쪽이 비워질 수 밖에 없음)
- 그 후 루트부터 Heap의 특성을 유지하기 위한 위치로 이동함
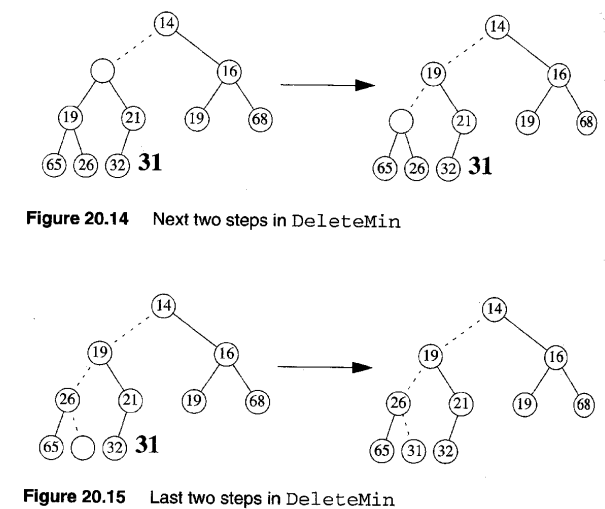
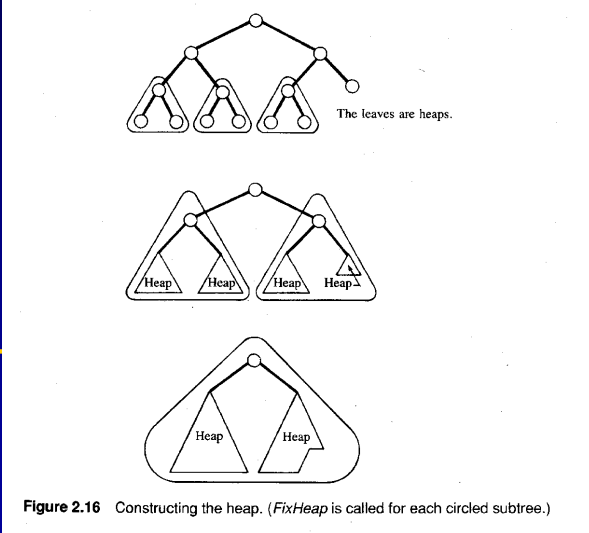
- Heap Construction
- 삭제후 루트에서 제 위치로 이동하는 과정에서 비교연산이 몇번 일어나는지
- 한번 이동할때 2번비교함(리프 중 더 큰/작은 리프를 찾는데 1번, 루트와 비교하는데 1번)
- 위의 기능으로 Heap을 divide and conquer로 만들 수 있음
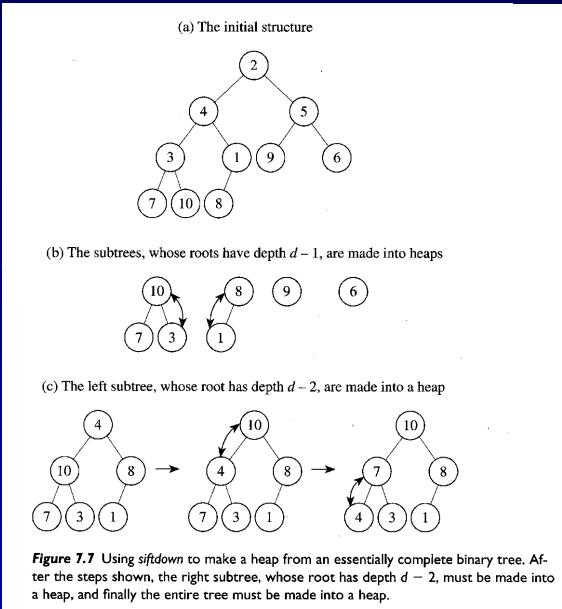
반복문으로 힙 construction하기
- 리프의 바로 위부터 시작
Heap Sorting
- 가장 간단한 방법
- n개의 데이터를 힙에 넣고
- delete min/max를 n번하면 정렬
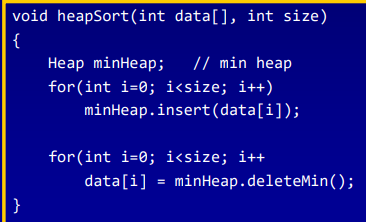
- delete하면서 정렬할때 배열이 1개 더 필요할거 같지만 1개만 있어도 가능함
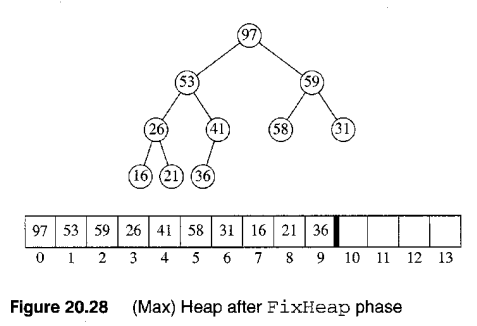
- max를 지우고 36을 root로 올린다음 fix할때 max(97)을 36자리에 주면 됨
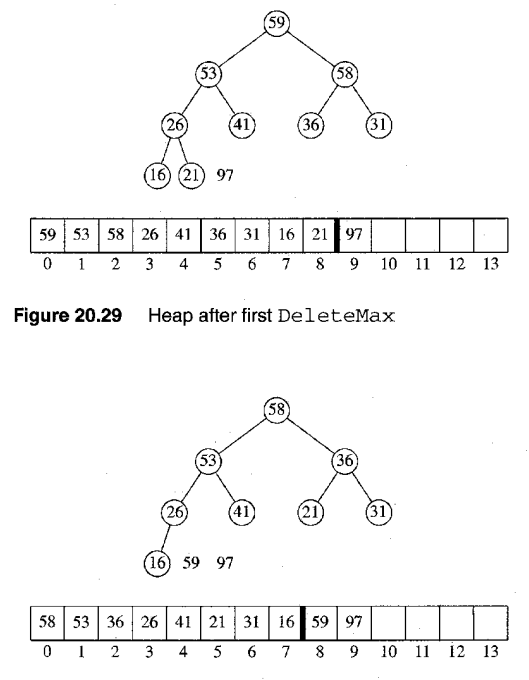
- 한번할때마다 마지막 자리가 비게 되고 그 자리에 정렬된 원소를 채우는 방식
- max힙일때 최대값이 제일 뒤로감, min힙은 최소값
Radix Sort
- 비교없이 정렬하는 방법
- 일정 범위를 설정하고 데이터들을 해당하는 범위로 지정하는 과정을 반복
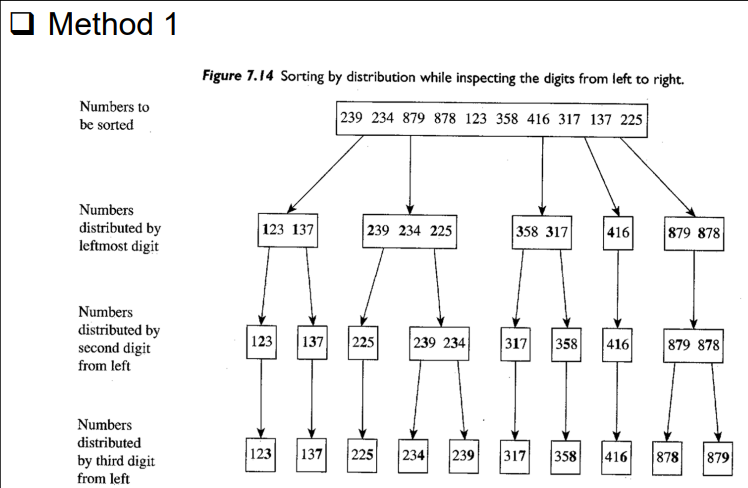
- 위는 100단위, 10단위 1단위 순서로 정렬한것
- 작은 단위부터 정렬하는 방법도 있음
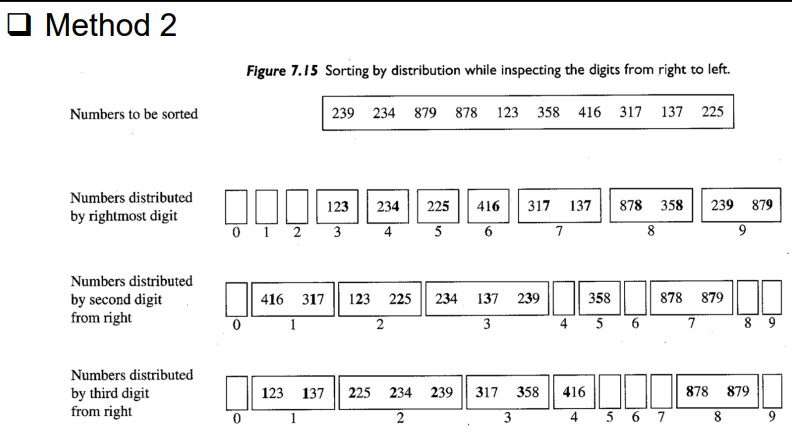
- 1단위로 정렬한 후 10단위로갈때 순서대로 옮기는것이 중요함
- O(n)만에 정렬가능, 비교를 하지 않고 정렬하기 때문에 LowerBound를 적용받지는 않음(적용받을 경우 nlogn이 제일 빠른 경우임)