정보보호 - 3(Cryptography - Hash)

Hash function
Cryptographic hash function
- m -> h(m) : 굉장히 빠름
- h(m) -> m : 불가능 해야함
- m != m1 = h(m)과 h(m1)은 1/2^256의 확률로 같음(사실상 불가능)
- m = m1일떄는 h(m)과 h(m1)은 반드시 같아야함
- 원본 메세지를 256비트의 해쉬메세지로 바꿈(SHA-256)
- 크기가 큰 원본 메세지 간의 비교를 하기 위해서 256비트의 2개의 해쉬메세지를 비교하기만 하면됨(메세지가 같으면 해쉬메세지도 같아야 하기 떄문)
원본 메세지를 여러 라운드를 거쳐 동일한 비트의 아웃풋을 출력함
Birthday attack
- 생일이 같을 확률
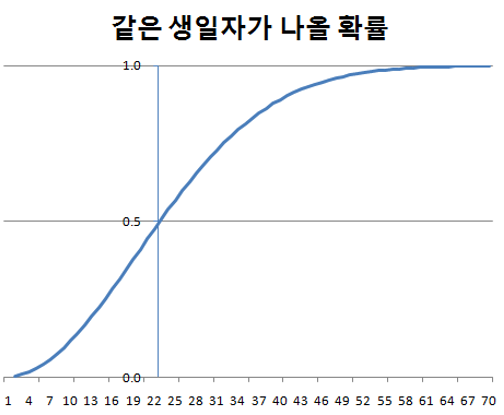
- 사람을 m 생일을 h(m)이라고 생각하면?
- m, m1에 대한 h(m), h(m1)이 다르기 위해선 해쉬함수의 결과가 길어야 한다(현재는 256비트 정도는 되야한다고 판단 중임)
Message authentication code(MAC)
- Integrity를 중요시 할때 필요
- 방송의 브로드캐스트 같은 경우 보안보다는 내용의 변조여부가 중요
- 대칭키의 CBC알고리즘이나 hash를 사용하면 구현 가능
- A -> B로 메세지를 보내는 경우
- m과 h(m||K_ab)를 보냄
- K_ab는 A와B만 아는 값이므로 m과 K_ab를 이어 붙인 h(m||K_ab)의 값은 A,B만 생성 가능
- A에서 보낸 h(m||K_ab)와 B에서 직접 계산한 h(m||K_ab)가 같아야 변조가 없는 것
- 추가로 보안까지 유지하고 싶으면 처음 m를 보내는 대신 K_ab(m)을 보내면 됨
One Time Password(OTP)
- Time-synchronized
- A(고객) -> B(은행) 이라하면
- OTP의 시리얼 넘버를 은행서버에 A의 정보에 입력(OTP에는 기기마다 고유한 키값이 있음), A는 OTP장비를 가져옴
- 인증이 필요할때 사용자가 OTP 기계를 사용 숫자를 생성(해쉬함수)
- OTP에는 시계가 있음
- OTP의 시리얼 넘버, 키, 시간을 concat해 해쉬함수를 생성 -> h(sn|key|time)
- 사용자가 은행에게 생성한 h(sn|key|time)과 은행에서 가지고 있는 정보로 h(sn|key|time)를 비교
- 전송시간을 고려해 특정 시간동안은 같은 해쉬값이 생성되도록 설정함(시간이 너무 길면 해킹 위험 -> Replay attack)
- Challenge-response
- 서버와 클라이언트가 공유하는 secret s가 있음
- 클라이언트가 로그인을 원하면 서버에서 챌린지 R을 클라이언트로 보냄
- 클라이언트는 R과S로 해쉬함수 H(R|S)를 만들어서 서버로 보냄
- 서버에서는 동일한 H(R|S)를 생성하고 받은 값과 비교함
- Hash chain
- 나만 아는 정보를 가지고 상대방에게 인증을 받고 싶어서 고안됨
- A -> B일때 A가 본인만 아는 랜덤 넘버 S를 생성
- A가 해쉬함수 H(S)를 생성
- 해쉬함수를 N번 적용 H(H(S))처럼 해쉬를 여러번 적용한 함수를 Hn(S))라고 함
- A가 N이 매우 큰 Hn(S)를 B에게 보냄
- B는 A와 Hn(S)를 저장, B는 S는 모르는 상태
- A가 로그인 할때 Hn-1(S)를 B에게 보냄
- B에서 H(Hn-1(S))를 계산해서 서버의 Hn(S)와 같은 값이 나와야 인증 성공임
- Hn(S)에서 Hn-1(S)로 가는것은 거의 불가능 하고 A만 생성 가능하기 때문에 가능한 방법
- 인증을 한번 하고나면 A는 n-2값을 보내고 B는 이전에 갱신해둔 n-1과 받은 n-2에 해쉬를 한번 더 적용해 n-1값을 만들어 저장해둔 값과 비교함
- n번만 사용 가능한 방법이라 주기적 갱신 필요


