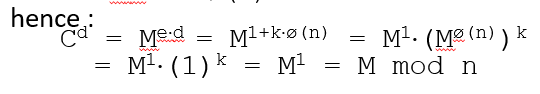asymmetric key(비대칭 키)
- Asymmetric key cryptography
- Diffie-Hellman
- RSA
- Korean crypto algorithms
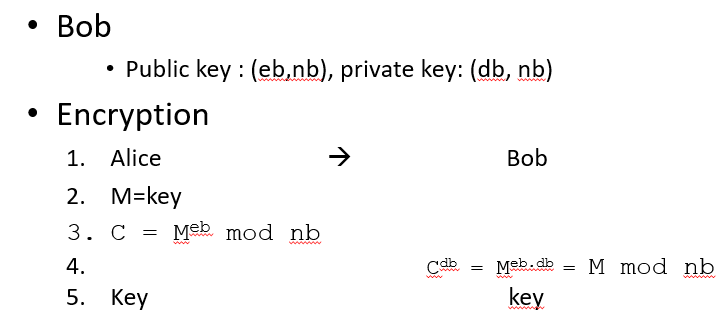
Asymmetric key cryptography
- 기존의 N^2의 시간을 NlogN으로 줄임
- 한 사람당 2개의 키를 가지고 시작
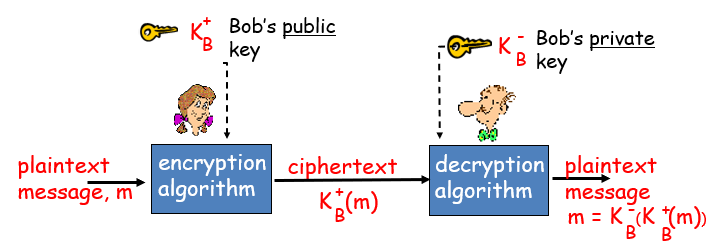
- A의 공개키는 Ka+ 개인키는 Ka-로 표기함
- A -> B로 보낼때 A가 B의 공개키로 암호화하고 이 메세지는 B의 개인키로만 해석 가능
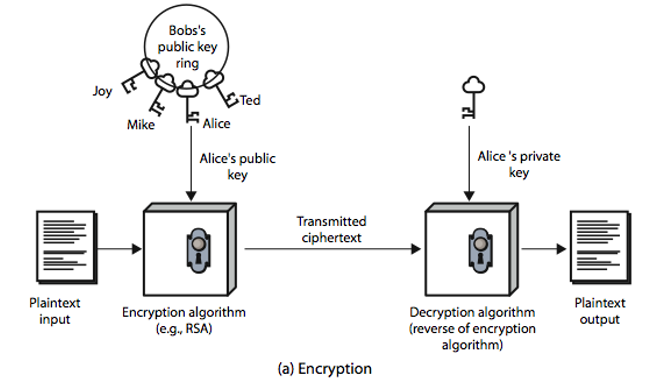
- 다른 사람의 공개키는 여러개 저장해두고 사용함
- 공개키 알고리즘은 계산이 느림
- 대칭키 알고리즘의 문제는 A와B간의 비공개키를 만드는 것이 문제였음
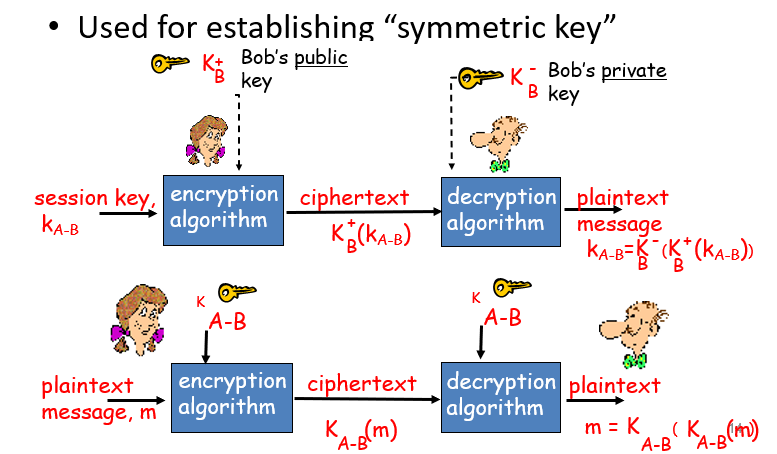
- 대칭키를 만들때 공개키를 활용하고 만든 이후 부터는 대칭키를 활용 하는 방법
- 전체 과정
- A -> B일때
- A가 B에게 요청하면 B는 B의 공개키를 보냄
- A가 Kb+(Kab)를 B에게 보냄
- Kb-(Kab)로 B가 Kab를 얻음
- A가 K_ab(m)를 B에게 보냄
- B가 Kab(m)으로 메세지 m을 얻음
- A는 Ka-(h(m))으로 m을 서명함
- Ka+(Ka-(H(m)))을 하면 H(m)이 나오고 이를 B가 받은 m으로 H(m)을 만들어서 비교가능
Diffie-Hellman
- 최초의 공개키 알고리즘
- 서명을 보장하지는 않음
- 과정
- A와 B가 각각 공개키 p,g를 가짐
- A가 랜덤한 본인만 아는 x를 생성
- A는 X = g^x mod p인 X를 B에게 보냄
- B는 Y = g^y mod p인 Y를 A에게 보냄
- A는 Y^x = g^xy mod p인 K를 계산
- B는 X^y = g^xy mod p인 K를 계산
- 서로 계산한 K의 값은 같아야 하고 이 값을 K_ab로 사용하는 방법
- 해커가 중간에 p,g,X,Y를 알 수 있지만 x,y는 알 수 없고 x,y를 모르면 K의 값을 수학적으로 현재로는 구할 수 없어서 보안성을 보장함
RSA
- 가장 많이 사용되고 있는 공개키 알고리즘
- 위의 수학적 사실중에서 a=b일때 곱셈을 활용한 방법
- 과정(A->B), A가 RSA키 Ka+,Ka-를 생성해야함
- A가 큰 소수 P,Q를 생성 n = PxQ이고 Ø(n) = (P-1)x(Q-1)
- 그리고 gcd(e, Ø(n))이 1인 e를 생성, e와 Ø(n)이 서로소 이어야함
- 1 < e < Ø(n)
- (e x d) mod Ø(n)이 1인 d도 생성해야함
- k x Ø(n) + 1 = ed
- e.d = 1 mod Ø(n)으로 표현
- 0<= d <= n
- 여기서 Ka+가 (e,n) Ka-가 (d,n)이 됨
- d가 A의 보안을 유지해주는 역할 외부에 공개되면 안됨
- 컴퓨터에서 보내려는 메세지 m은 결국 바이트이기때문에 매우큰 숫자라고 생각할 수 있음
- 위에서 (m^e) mod n을하면 n보다 작은 숫자가 되고 이 값이 Ka+(m)이 됨 -> 암호화
- 복호화(Ka-(Ka+(m))) -> (m^e mod n)^d mod n을 하면 m이 나옴
- (m^e mod n)^d mod n -> m^ed mod n -> m mod n,, m이 n보다 작거나 m을 n보다 작게 쪼개서 해야함
- 페르마의 소관계로 입증, 서로소인 a,p에 대하여 (a^p-1 mod p = 1)
- 1xa mod p, 2xa mod p, 3xa mod p... (p-1)xa mod p에 대해 모든 값이 다름
- 위에 값중 아무거나 2개가 같다고 가정했을때 (j-i)xa가 p로 나누어 떨어지는 j,i를 찾아야 함 j-i가 항상 p보다 작고 a는 p와 서로소 이기때문에 나누어 떨어질 수 없어서 증명됨
- (1xa x 2xa x 3xa ... (p-1)xa) mod p = 1x2x3...x(p-1) mod p이고 양변을 (p-1)!로 나누면 a^p-1 mod p = 1 mod p가 됨 -> 이 식이 복호화에 사용되는 것
- https://ko.wikipedia.org/wiki/%ED%8E%98%EB%A5%B4%EB%A7%88%EC%9D%98_%EC%86%8C%EC%A0%95%EB%A6%AC
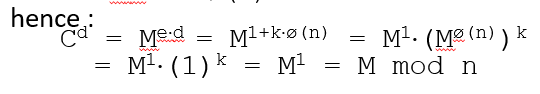
- (m^e mod n)^d mod n을 페르마의 소정리를 활용해서 m이라는것을 증명하는 것이 핵심
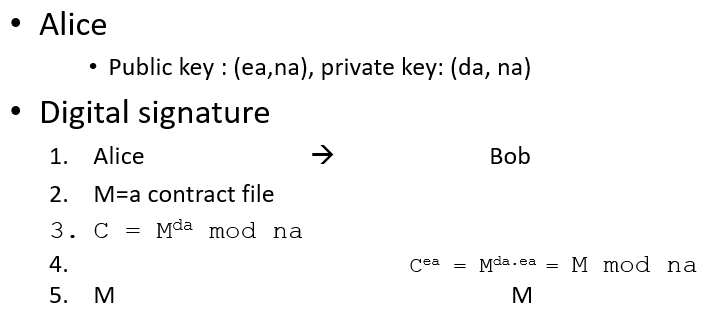
RSA 서명과 검증
- 서명 : Ka-(m) : m^d mod n
- 검증 : Ka+(Ka-(m)) : (m^d mod n)^e mod n -> m^ed mod n -> m mod n -> m
- sample
- p = 17, q = 11, n = pxq, 17x11 = 187, Ø(n) = (p-1)(q-1) = 16x10 = 160
- e = gcd(e, 160) = 1, choose e = 7
- d: de mod Ø(n) = 1 and d<160 d = 23일때 de = 161이고 161 mod 160 = 1
- (7,187) -> 공개키, Ka+
- (23, 187) -> 개인키, Ka-
RSA 암호화, 복호화 및 서명
- 암호화,복호화
- 서명
공개키, 대칭키, 해쉬함수 과정 정리
- 기밀성, 무결성, 부인봉쇄, 효율성을 만족해야함
- A -> B일때
- A가 B에게 요청하면 B는 B의 공개키를 보냄 (1)
- A가 Kb+(Kab)를 B에게 보냄
- Kb-(Kab)로 B가 Kab를 얻음
- A가 K_ab(m)를 B에게 보냄 -> 기밀성 보장
- B가 Kab(m)으로 메세지 m을 얻음
- A는 Ka-(h(m))으로 m을 서명해서 보냄(효율성을 위해 m이 아닌 h(m)에 서명) -> h(m)으로 무결성과 부인봉쇄를 보장
- Ka+(Ka-(H(m)))을 하면 H(m)이 나오고 이를 B가 받은 m으로 H(m)을 만들어서 비교가능
- A가 B의 공개키를 받은 후 B에게 보내는 3가지는 하나씩 보내는 것이 아니라 한번에 보내고 B가 한번에 받는 방법임
- 위 과정에서 해커가 B인척 하고 본인의 공개키를 B의 공개키로 속여 A에게 보내면 문제가 생김
- A가 받은 공개키 Kb+가 헤커가 아닌 B의 공개키가 맞는지 확인하기 위해 CA(공인 인증기관)사용 -> CA도 공개키, 개인키 Kc+,Kc-를 보유
- B가 인증서를 요청하면 CA에서 CA의 개인키로 B의 공개키를 서명해서 B에게줌 -> Kc-(Kb+,B), B는 B를 판별할 수 있는 정보
- 이제 위의 첫번째 단계에서 B는 B의 공개키 Kb+가 아닌 Kc-(Kb+,B)를 보냄
- A는 B에게 받은 Kc-(Kb+,B)를 Kc+(Kc-(Kb+,B))를 통해 Kb+와 B를 얻음
- 해커(m이라 하면)가 CA를 통해 Kc-(Km+,m)까지 받고 Km+는 단순한 바이트이기 때문에 Kb+인척 속이기 까지는 가능하지만 Kc-(kb+, B)의 B는 따라할 수 없음
- Kc-(kb+, B)를 해커가 Kc+로 해독해서 가로챌 수 있을것 같지만 검증은 A가 직접 Kc-(kb+, B)를 Kc+로 검증하기 때문에 Kc-를 절대 모르는 해커는 피싱이 불가능함
- 추가로 A도 Kc-(Ka+, A)를 공인인증기관에서 발급받아 B에게 보내주어야 함
KMU SW