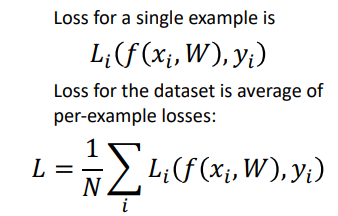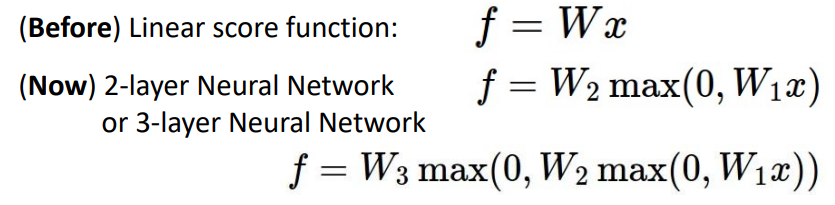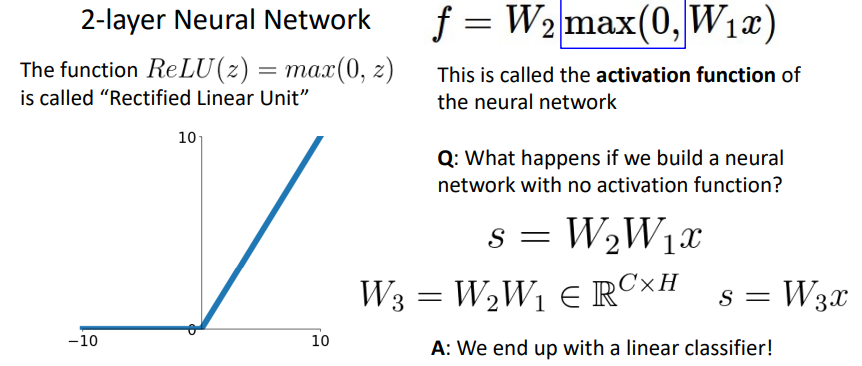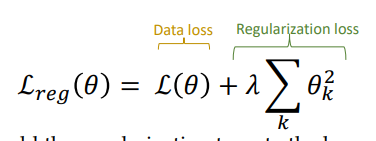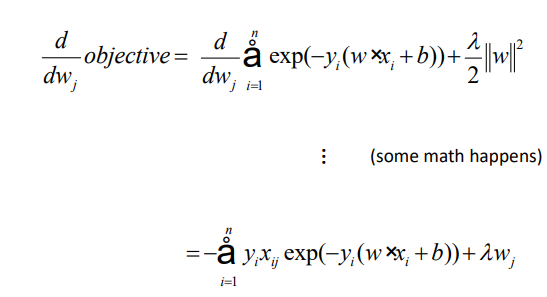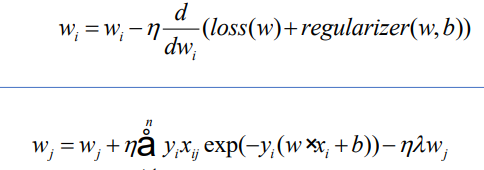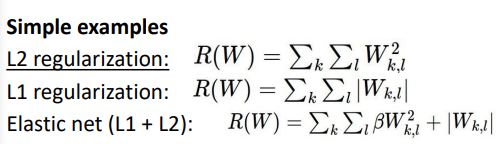딥러닝 _intro
학습
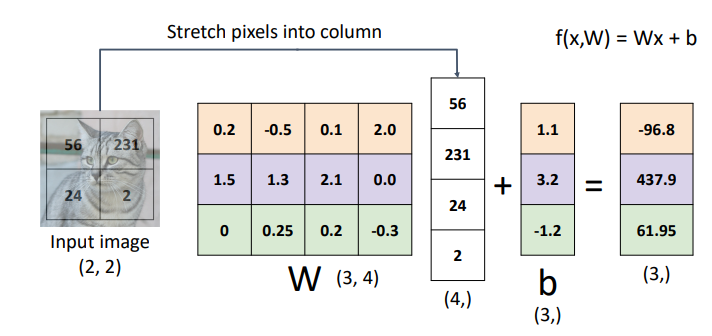
- W의 값들을 잘 조정해서 원하는 결과가 나오게 하는 것
- 많은 데이터를통해 w를 갱신해가는 과정이 학습임
- b가 없으면 직선이 원점을 반드시 지나야 하기 때문에 한계가 있음
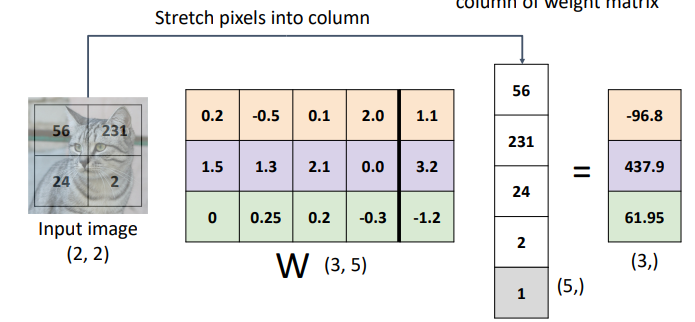
- 원점을 지나지 않는 직선은 linear하지 않다
- b를 더하는 대신 w에 차원을 추가하는 방식으로 linear성질을 유지할 수 있음
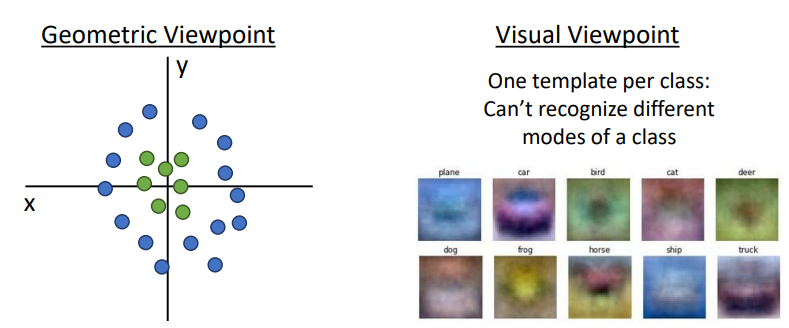
템플릿 매칭
- 주어진 데이터(이미지)와 기존의 템플릿을 활용해 결과는 내는 방식
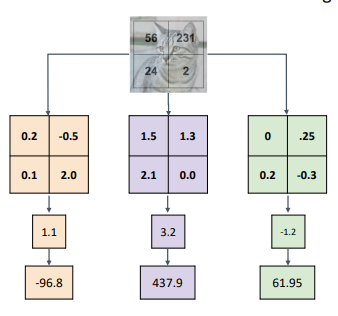
- 템플릿과 기존의 이미지의 모양이 비슷해야 아웃풋 값이 커짐
- 위의 선형 학습은 템플릿 매칭중 하나라고 생각할 수 있음
- 데이터의 개수가 매우 많아지면 그 모든 데이터에 매칭되는 템플릿을 찾는 과정에서 템플릿이 계속 뿌옇게 변해가기 때문에 한계가 명확함, 그래서 딥러닝을 사용
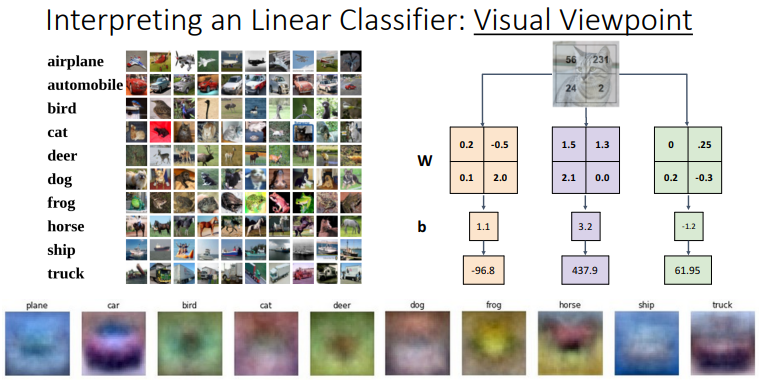
- 말(horse)템플릿의 경우 말이 양쪽을 보고 있는 것처럼 보이는데 많은 데이터를 모두 만족시키기 위해서 나온 현상임
학습의 과정
- w를 찾아야 함
- loss function을 정의하고
- optimization으로 이를 최적화함
- loss function
- 현재의 모델이 얼마나 좋은지를 평가하는 지표
- loss가 낮으면 좋은것(loss는 정답값과 떨어져있는 정도임)
- loss를 최소화하게 만드는 w를 찾는것이 학습
- 정답값은 미리 주어져야함
- 모든 x에대한 결과값 y에대한 데이터 셋이 필요
- ex) 이미지 x 1번의 y y1은 1(정수로 표현)
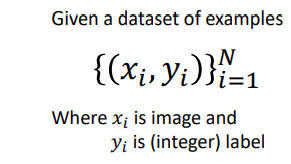
- 우리 모델의 아웃풋과 정답값의 차이를 정의
- 위에서 주어진 x에 대한 우리가 정의한 함수를 적용시켜서 나온 결과값과 위에서 주어진 같은 x에대한 정답값 y과의 차이를 구함
- 차이값은 x의 개수만큼 나오게되고 최종 loss값은 일반적으로 평균값으로 선택
- 모든 x에대한 결과값 y에대한 데이터 셋이 필요
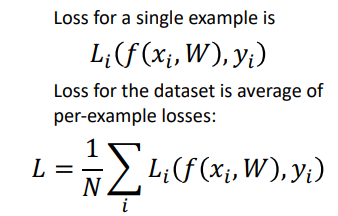
- 소프트맥스함수로 확률로 변환(기존값을 e의 지수로 올려서 다 더해서 분모로 보내고 각각의 값은 각각의 값을 e의지수로 올려서 분자로 보냄)
- 0.13이 정답 클래스에 대한 확률값임 0.13이 1이 될때 -log함수는 0이되기때문에 loss값이 최소가 됨
- 확률값을 1로 만드는(loss가 최소가 되게 만드는 w를 찾아야함)
DNN
- 데이터의 모양이 non-linear일때 사용
- DNN이 아니여도 Feature transform으로 non-linear데이터셋을 linear로 해결이 가능하긴함
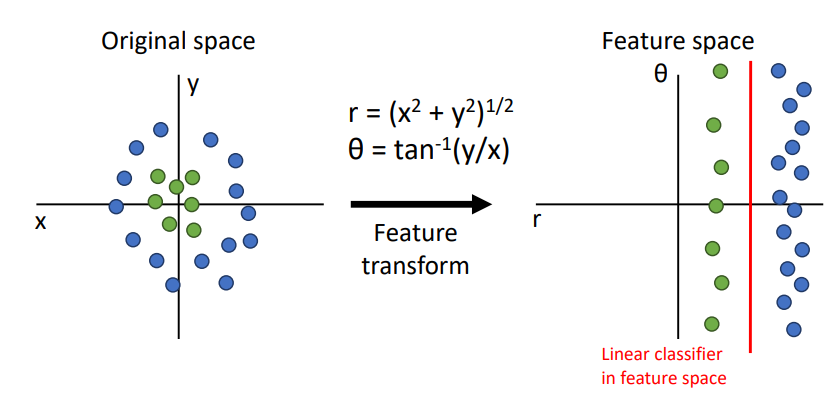
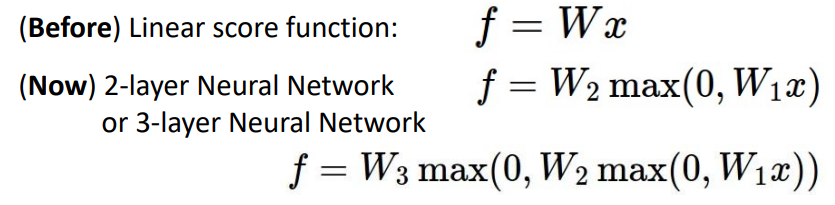
- 이는 feature가 만족하는 형태로 만들어질때까지 여러가지로 변환해봐야하는 단점이 있음
- 추가로 결국에는 원래의 모양(x,y좌표)은 non-linear라는 단점도 있다.
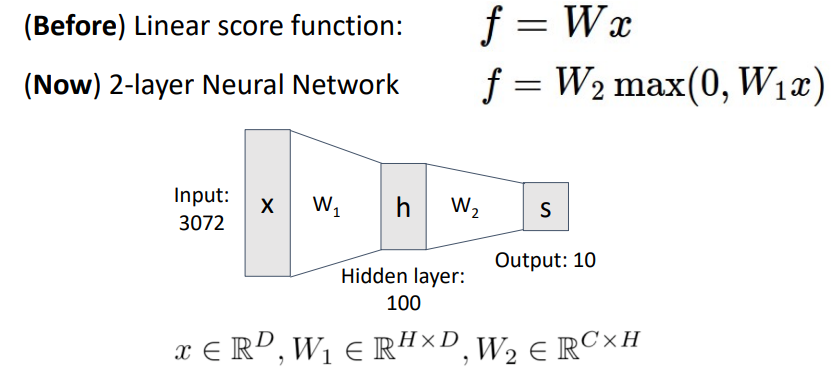
- Neural Networks(non-linear문제 해결)
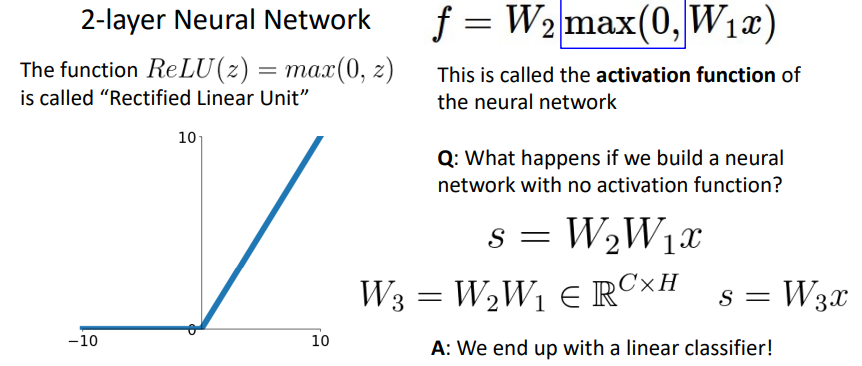
- max를 취하는 이유 -> linear의 특성을 피하기 위해
- max로 0보다 작은 값을 제거하면서 순서성을 부여하고 이는 결합법칙을 깨기때문에 linear의 특성을 깨버림
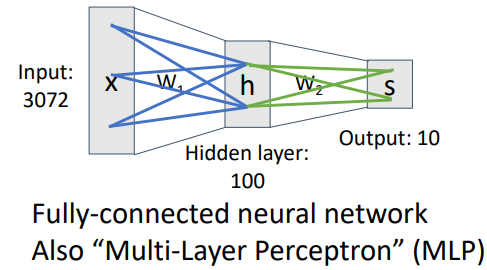
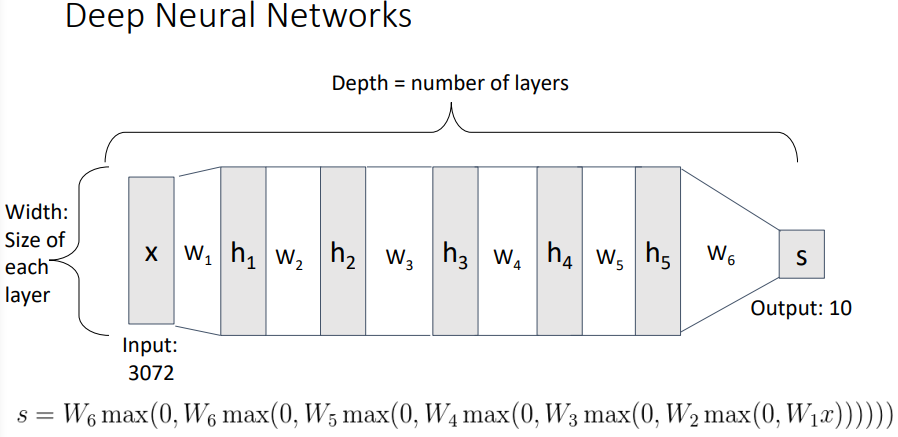
- w의 개수에 따라 n-layer Neural Network라고 표현
- Fully-connected(모든 데이터가 행렬곱셈에서 참여하는 것)
- 레이어마다 계산된 값을 그다음 레이어에서 사용하고 중간중간 max함수로 0으로 만들어버리기 때문에 해석과 추적이 불가능함
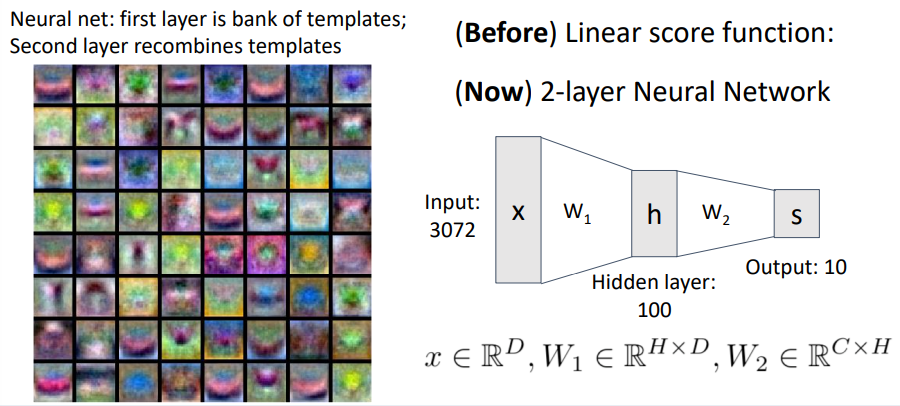
- 레이어가 많을수록 분별력이 높아짐
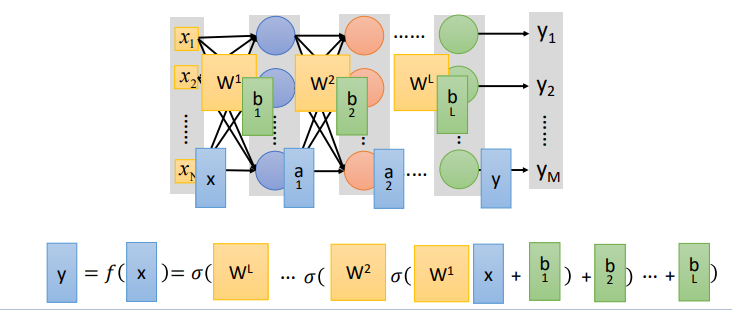
레이어를 찾아가면서 output을 내는것이 딥러닝(Deep Neural Networks)
Regularization
- 위에서 레이어의 개수와 분별력은 비례한다고 하였음
- 레이어가 많을떄의 단점도 있다(over-fitting)
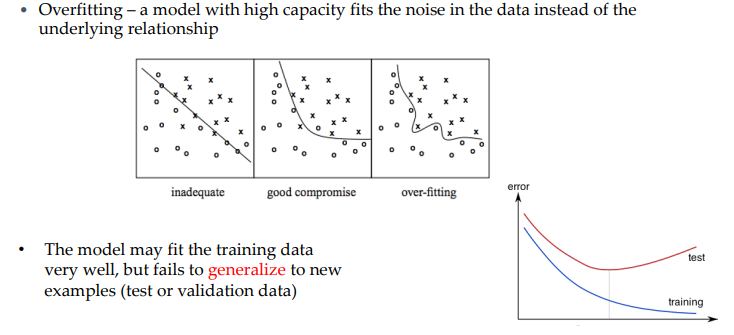
- over-fiting은 train데이터(실험용)과 test데이터(실제 사용시의 데이터)간의 차이에서 문제가 발생함
- train데이터에 너무 맞춰두면 실제 데이터에는 못 맞추는 경우가 늘어날 수 있음
- 결국 train데이터는 많아질수록 에러가 적어지지만 test데이터의 양은 많아지면 에러가 많아질수 있음
- over-fitting을 피하기위해 사용하는 것이 정규화(Regularization)
- loss값에 더해져서 loss펑션 자체를 바꾸는 것이 정규화
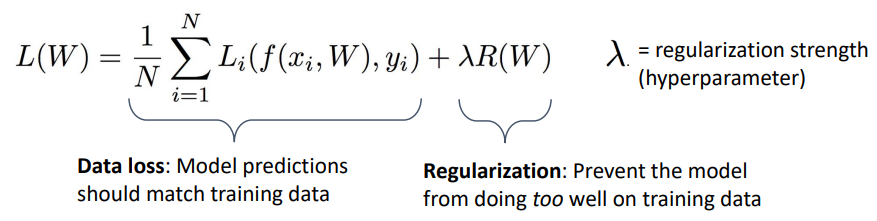
- loss펑션에 붙어서 피팅을 방해해 오버피팅을 완화
- w에서 각각의 값이 너무 크거나 작으면 x각각에 대한 의존도가 높아짐(w의 range를 줄일 필요가 있다 -> regularizer사용)
- Regularizations
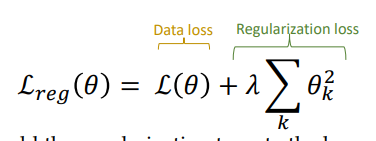
- loss를 데이터, 정규화 loss 2가지로 나눠서 컨트롤
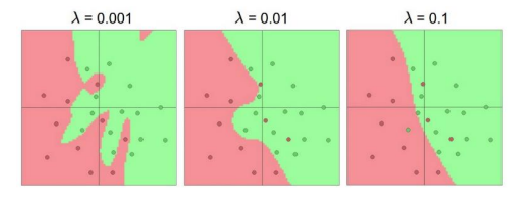
- 오버피팅을 피하는게 목표라면 람다값을 높이면 됨
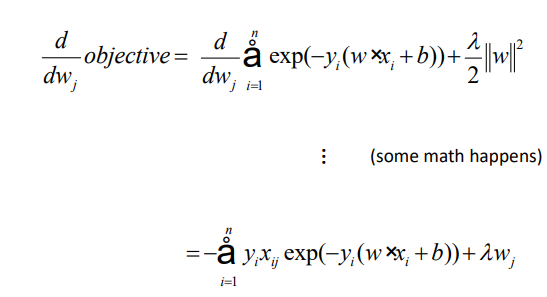
- 레귤라이저 부분이 j에 해당하는 wj에 대해 미분이 되어서 람다wj만 남게 됨
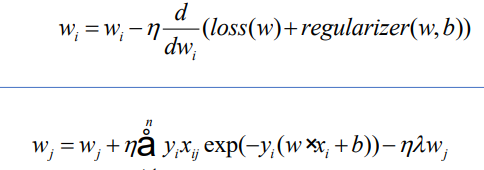
- 앞에 있는 -가 데이터로스, 레귤라이저로스에 붙음
- n은 러닝레이트
결론
- L2 norm
- 업데이트과정에서 미분을 사용
- 레귤라이저가 음수면 더하는 값은 양수가 되고 레귤라이저가 양수면 더하는 값은 음수가 됨
- 결과값의 절대값의 크기가 작아짐
- L1 norm
- 1보다 크면 1, 작으면 -1인 절대값 함수의 미분을 위해 sign함수를 사용
- 미분하면 양수면 1, 음수면 -1이 나옴
- 결국에 앞에 -를 붙이기 때문에 갱신시 절대값의 크기가 작아지는것은 동일
L1, L2 norm의 차이
- L1은 1,-1만큼만 이동하고 L2는 본인의 값을 곱해서 이동
- L2는 본인의 값을 곱하면서 본인의 값을 줄이기 떄문에 이동하는 거리가 점점 작아짐(non sparse)
- 0에 매우 가까워지긴 하지만 0이되지는 않음
- L1은 Spaese한 특성이 있음
- 실제로 0을 만들 수 있음, L2에 비해서 학습을 거듭하면 0을 만드는 횟수가 많아짐
연결선의 행렬 변환
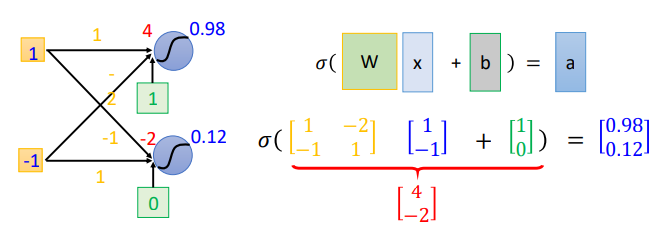
- 왼쪽의 연결선을 오른쪽의 행렬의 곱으로 옮길 수 있음
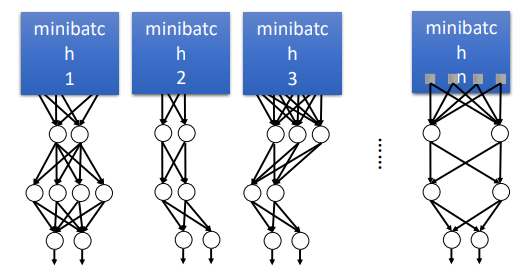
Dropout
- 정규화의 방법중 하나
- 딥러닝의 각 계층(레이어)에서 연결선이 너무 많으면 계산이 정확해서 결국 오버피팅 효과가 발생함
- 연결선의 일부분을 지워버려 과도하게 미세한 계산을 피하는 방법이 Dropout
- 지우는 행렬의 값을 0으로 만들어 반영이 안되게 함
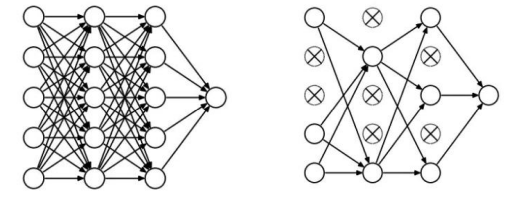
- 앙상블 효과가 있다
- 랜덤하게 연결선을 지우기 때문에 다양한 모양이 나와 성능이 향상된다
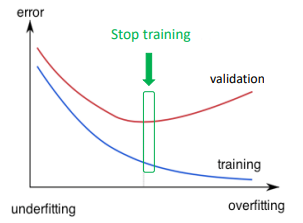
Early-stop
- 오버피팅 되기전 학습을 중지하는 것
- validation : test데이터를 활용하기 어렵기 때문에 train데이터의 일부를 학습전에 분리해 test데이터처럼 활용 하는 것
Activation Functions
- 종류가 여러개가 있다, 상황에 맞게 종류를 결정해야함
- 중요한 것은 non-linear성질을 다루기위해 사용한다는 것
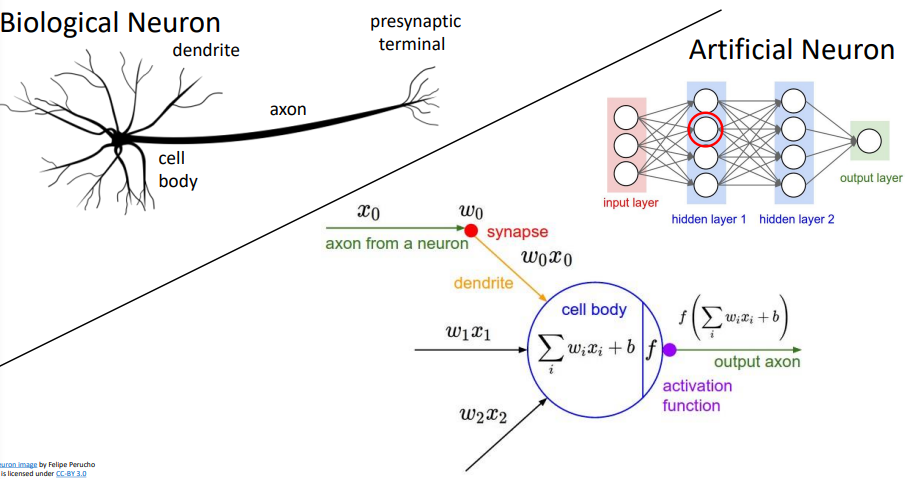
생물학적 뉴런과 유사
KMU SW