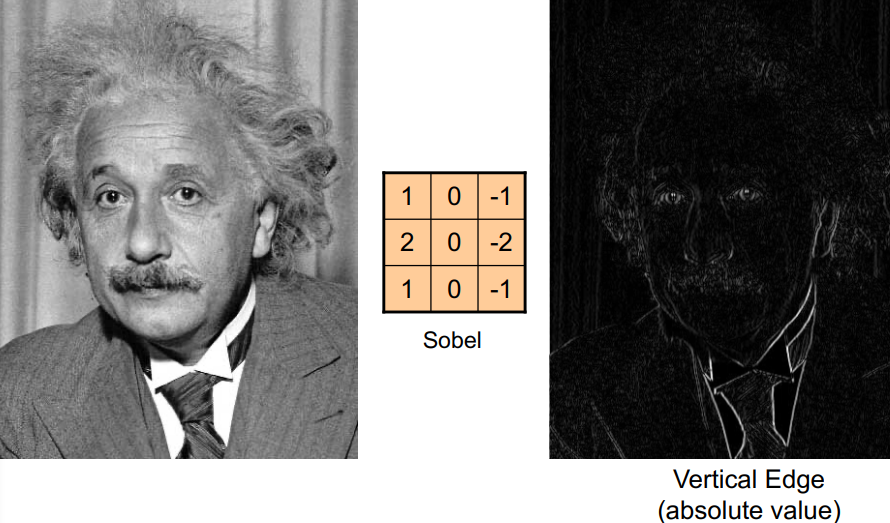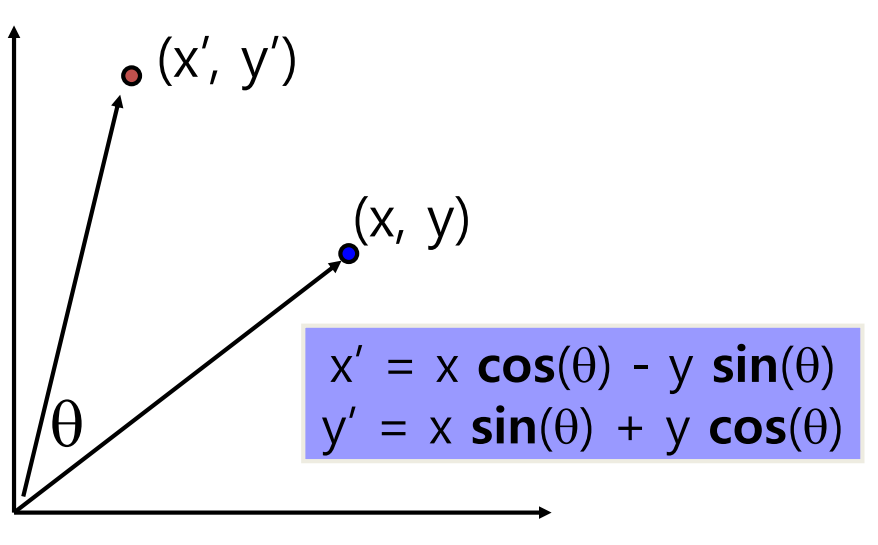연산
영상 처리의 세 가지 기본 연산
- 점 연산 : 오직 자신(픽셀)의 명암값에 따라 새로운 값을 결정
- 영역 연산 : 이웃 픽셀의 명암값에 따라 새로운 값 결정
- 기하 연산 : 일정한 기하 연산으로 결정된 화소의 명암값에 따라 새로운 값 결정
점 연산
- 선형 연산 : +,-를 활용한 연산
- 비선형 연산 : 감마 수정(모니터, 프린터의 색상 조정에 사용)
- 특정 구간의 명암을 많이 변화 시키거나 적게 변화 시키는 방법
- 디졸브 : 영화의 페이드 인, 페이드 아웃
- 화면 전환을 0~1 사이의 알파 값을 사용해 한번에 전환 하지 않고 자연스럽게 넘어가도록 하는 방법
- f1에서 f2로의 전환
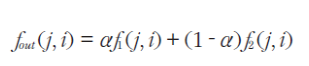

영역 연산(필터링)
- 2차원 영상에서의 연산
- Smoothing, sharpening, measuring texture의 효과
- 각각의 픽셀에 대해서 그 주변의 픽셀의 정보를 활용한 연산 방법
- 패턴 추출, 화질 증가 등에 활용 가능
- 상관(correlation)
- 입력 영상에 주어진 윈도우(필터)를 씌우는 방식
- 영상의 한 픽셀마다 윈도우의 중앙을 맞춤
- 윈도우와 영상의 같은 위치에 있는 값을 각각 곱하고 더함
- 모두 더한 값이 처음 고른 영상의 한 픽셀의 값이 됨
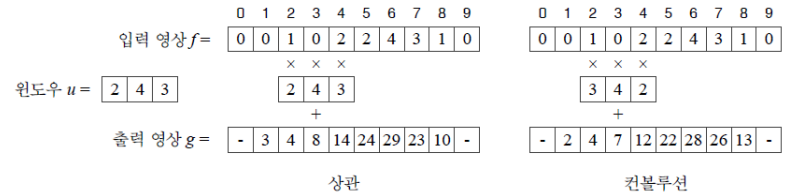
- 1차원에서의 상관 연산
- 입력 영상에 주어진 윈도우(필터)를 씌우는 방식
- 컨볼루션
- 윈도우를 뒤집은 후에 상관을 적용
- 2차원 상관 연산
- 입력 영상의 값이 0이어도 주변의 값에 따라 픽셀이 바뀔 수 있음
- 윈도우의 중앙에 맞추고 연산 후 해당 결과를 한 픽셀에 적용 하는 방법은 동일 함
- 상관, 컨볼루션의 차이
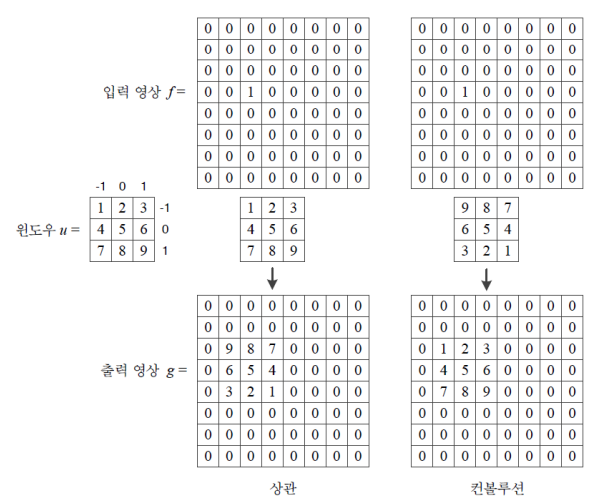
- 상관은 연산 후 결과값이 윈도우와 반대로 나옴
- 윈도우의 특성을 그대로 적용 시키기 위해 윈도우를 뒤집은 후 연산하는 컨볼루션이 존재하고 더 많이 사용함
- 컨볼루션 예제
- 박스 필터 : 주변 픽셀들의 평균값으로 바꾸는 역할 -> 주변과의 경계를 줄여줌
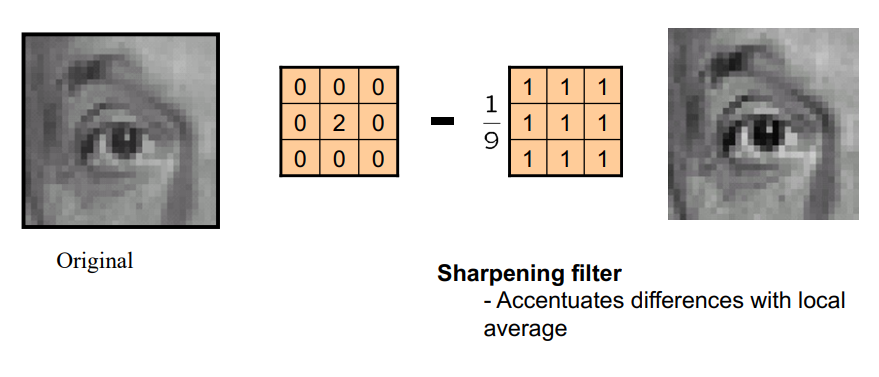
- 샤프닝 필터 : 내가 가지고 있는 픽셀은 강조, 주변은 감소 -> 주변과 내 자신의 경계를 뚜렷하게 함
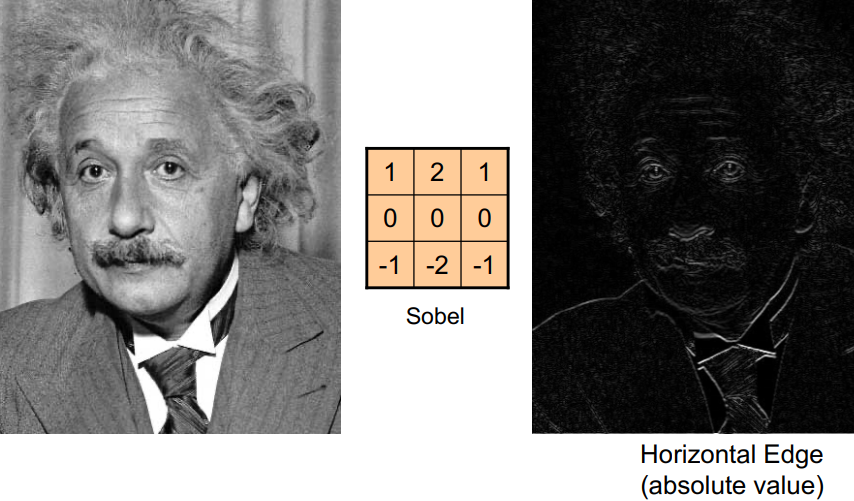
- 수평 엣지 : 세로 방향의 변화를 강조
- 수직 헷지 : 가로 방향의 변화를 강조
- 모션 : 움직임의 느낌

- 박스 필터 예시
- 윈도우의 넓이 만큼 나누어 평균을 구해서 적용하는 방식(윈도우가 3x3이면 9로 나누어야 함)
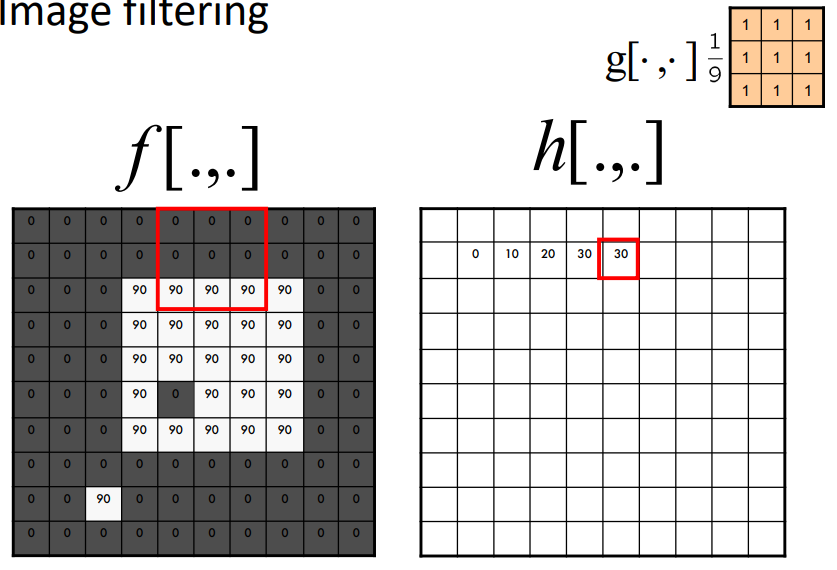
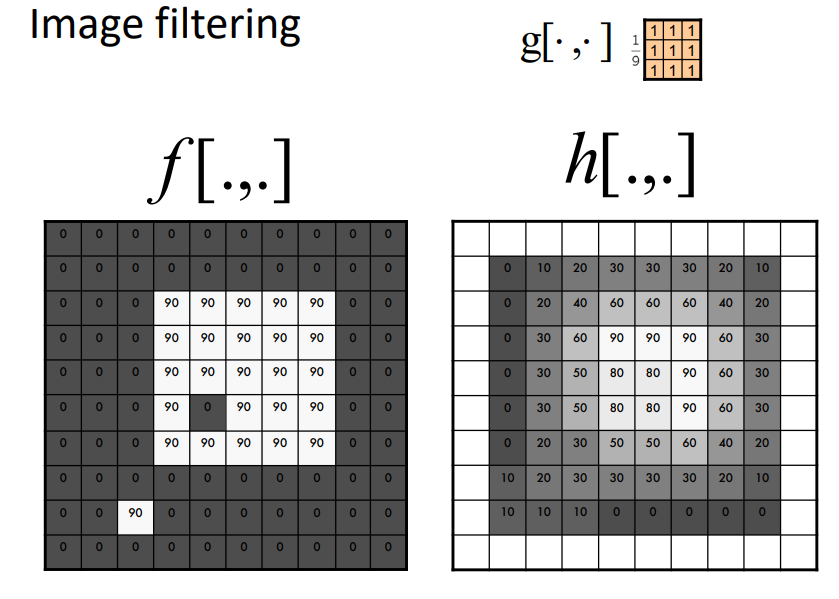
- 주변의 영향을 받아 명암차이가 큰 구간으로 가는 과정에서 중간 단계가 생기는 현상(모자이크의 대표적인 방법)

linear filter
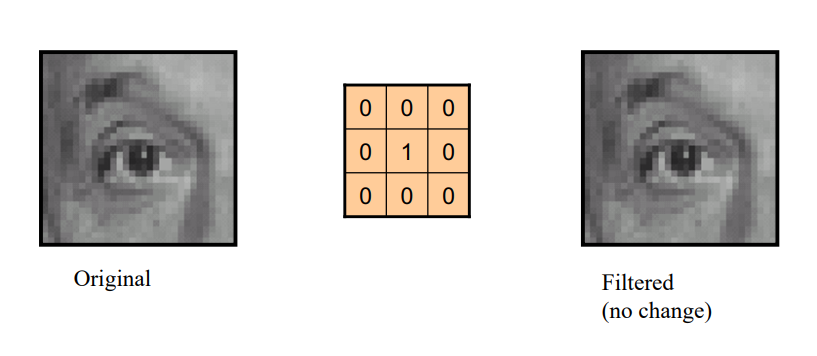
- 본인 값을 그대로 적용 : 변화 없음
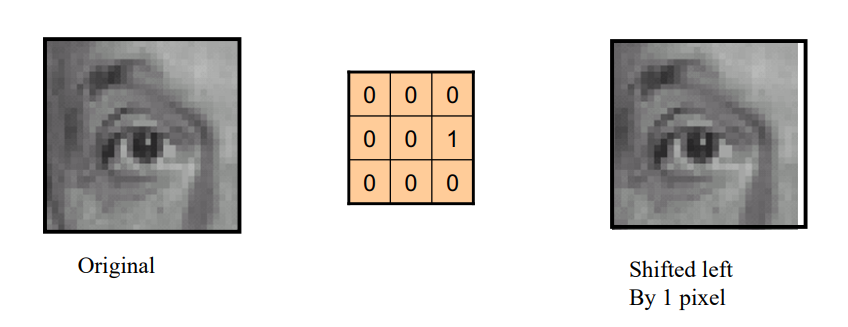
- 오른쪽의 픽셀을 가져옴(왼쪽으로 이동)
- 본인 값을 강조
- 수직 변화 강조
- 수평 변화 강조
리니어 필터의 특징
-
선형적 특징 유지
-
이동시키는 과정도 문제 없음
-
필터의 적용 순서와 상수의 곱에도 영향이 없음
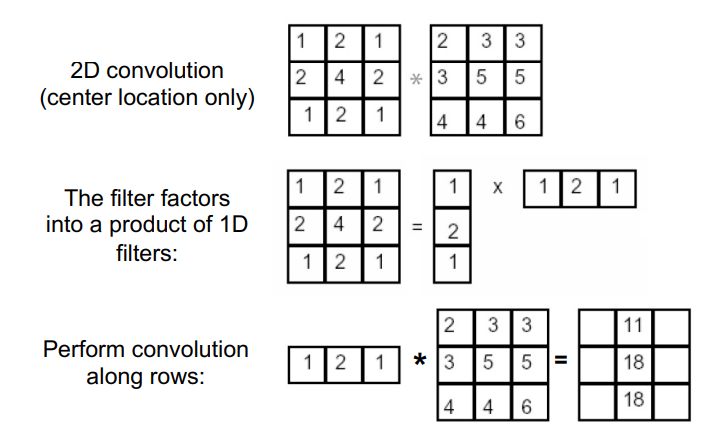
가우시안 필터
- 박스 필터와 같은 역할을 하지만 박스 필터에서 생기는 격자무늬를 줄여줌
- x축 y축에 가우시안 필터를 각각 두번 적용하는 것과 한번에 2차원에 적용하는 것은 효과가 동일함
- 1차원 필터를 x, y로 따로 적용하여 처리 시간을 줄일 수 있음
비선형 필터
- 메디안 필터
- 검정, 흰색의 잡음(0 or 255의 명암값) 제거에 효과적임
- 가우시안은 모든 값을 반영해주지만 메디안은 중간값을 사용하기 때문에 0, 255의 잡음 제거에 효과적

기하 연산

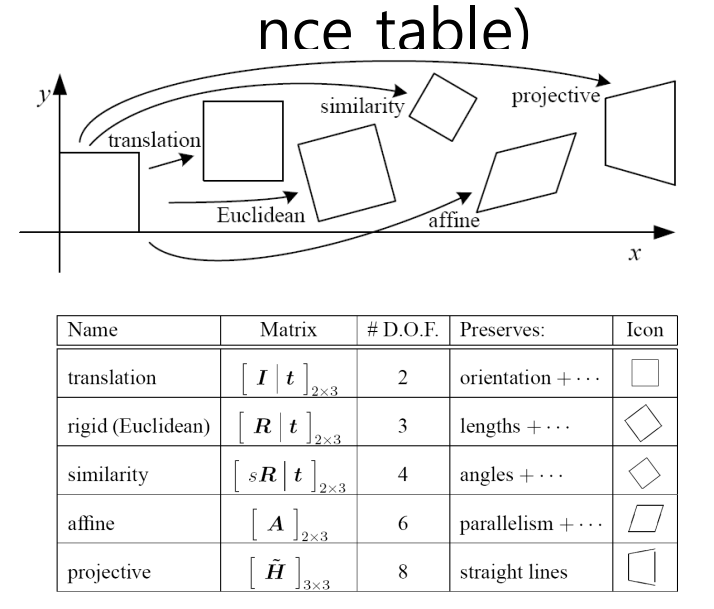
- 원본영상에 매트릭스를 곱해 변화시킴, DOF는 변화되는 요소의 개수
- affine : 각도까지 변화, 마주보는 선분의 평행은 유지
- projective(perspective) : 평행까지 깨짐
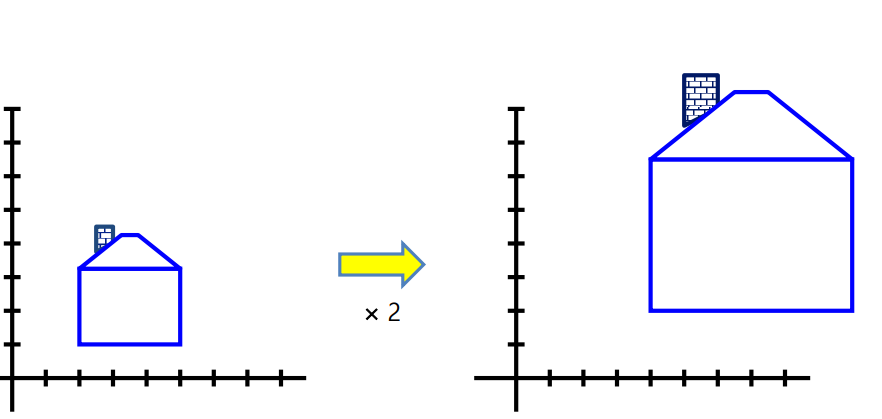
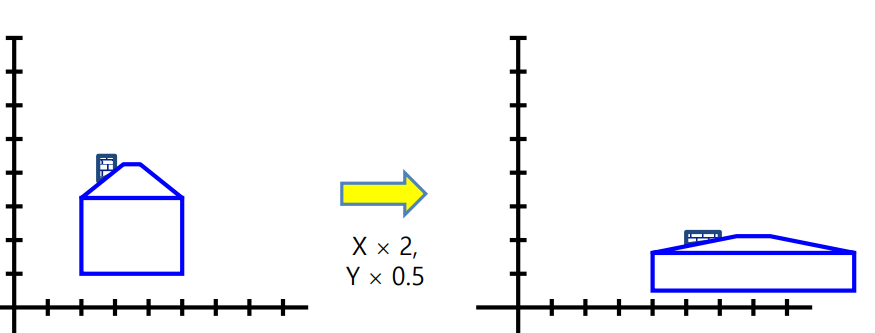
Scaling
- Uniform scailing : x,y축이 동일한 변화를 하는 경우
- Non-Uniform scailing : x,y축이 각각의 배율로 변화함
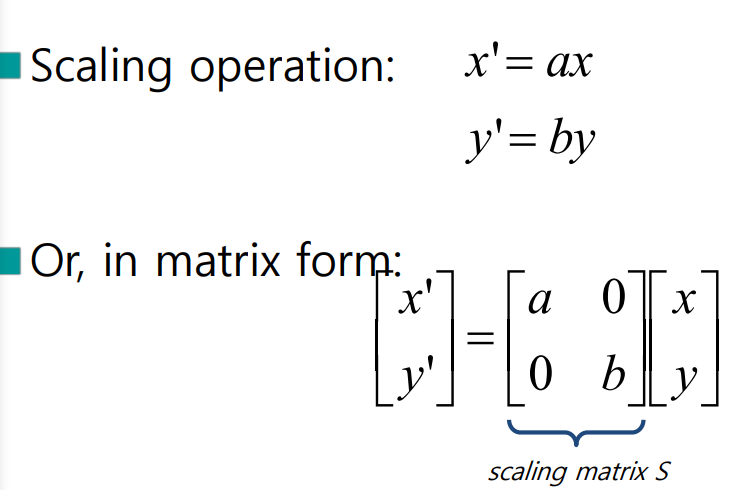
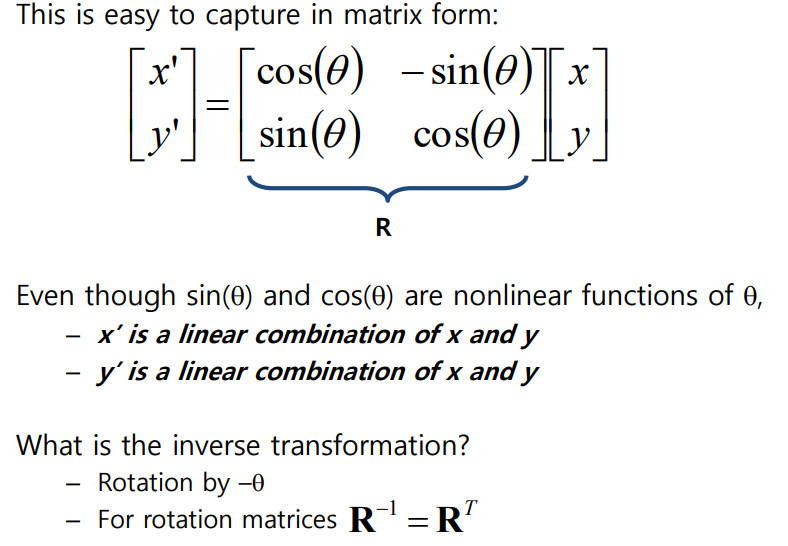
2-D Rotation
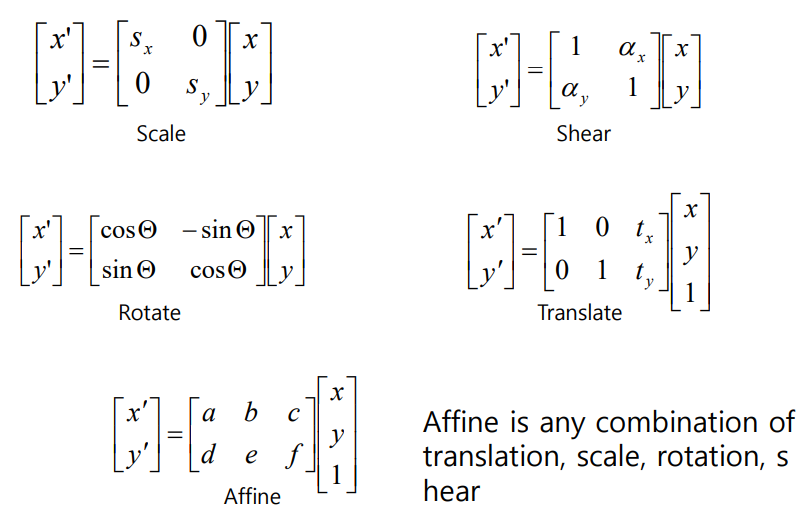
Basic 2D transformations
- Affine은 다른 여러가지 계산의 조합이다
- Affine Transformations
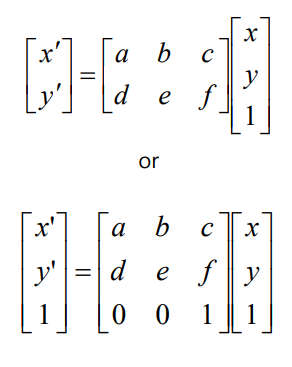
- 평행선은 유지 됨
- Projective Transformations
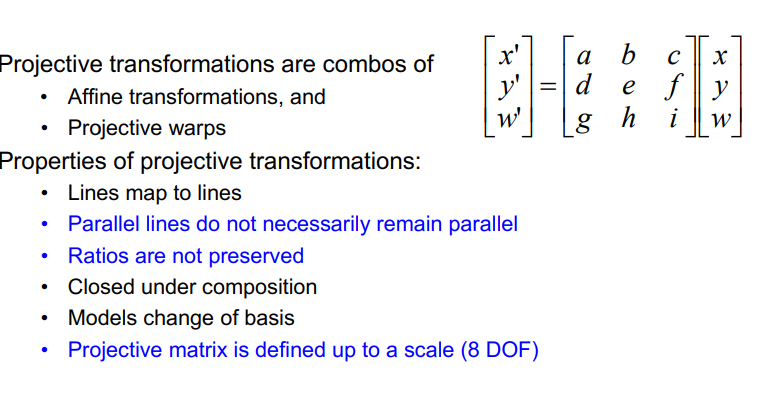
- 보통의 3d를 2d영상으로 옮길떄 사용
- 3x3의 행렬을 사용
동차 좌표와 동차 행렬
- 동차 좌표 :
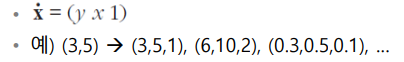
- 동차 행렬 :

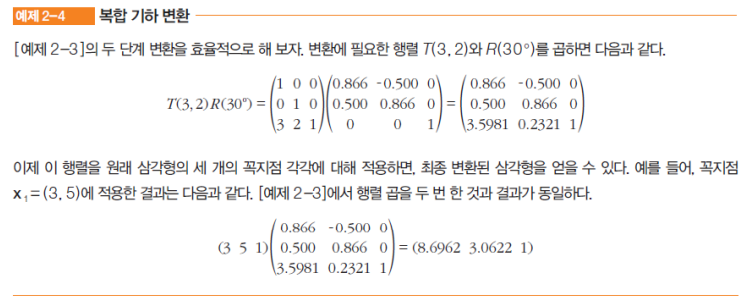
- 동차 행렬을 이용한 기하 변환 예시

- 2가지 변환(이동 후 회전)
- 동차변환을 사용하는 이유
- 복합 변환(2가지 이상의 변환)시 이동 후 회전시 필요한 두 번의 행렬 곱셈을 한 번의 곱셈으로 해결 가능
에일리어싱, 안티 에일리어싱과 보간
- 전방 변환, 후방변환
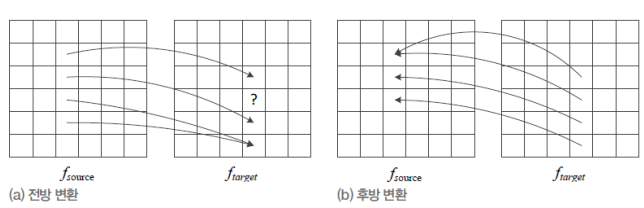
- 변환 시 겹치는 점이나 비어있게 되는 점(에일리어싱) : 비는 점은 검은색, 겹치는 점은 평균값으로 적용시켜 영상이 어색해지는 현상(계단 현상)이 발생함
- 보간에 의한 안티 에일리어싱
- 스케일 x' = 2x, y' = 2y의 과정에서 빈 공간이 생김(0,0, 0,1, 0,2대입 해보면 0,3등이 빈공간)
- 빈 공간은 주변 픽셀을 이용한 보간으로 안티 에일리어싱함
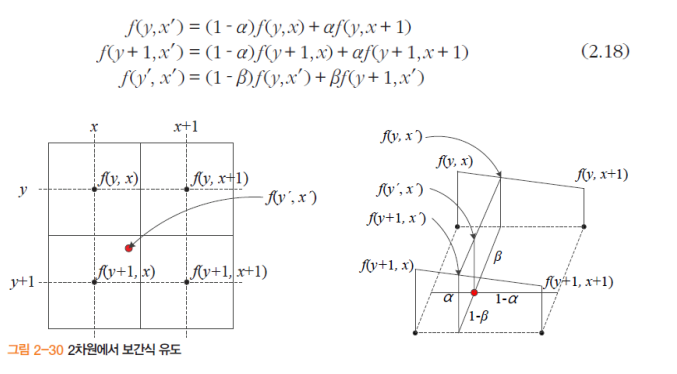
- 양선형 보간
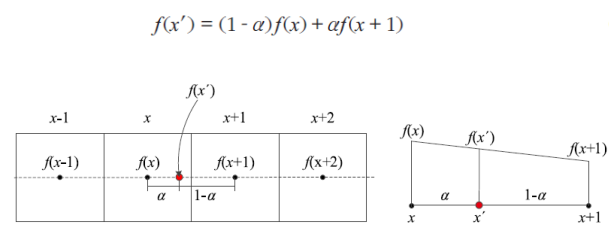
- 평균값이 아닌 웨이트 값을 설정해 차등비율로 적용함
- 2차원의 양선형 보간
- 보간 결과
다해상도
- 해상도를 줄이거나 늘리는 영상
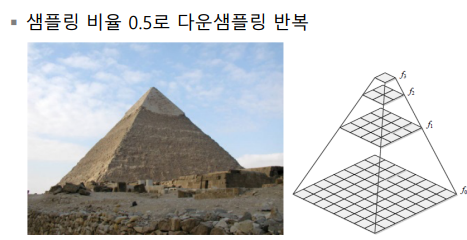
- 피라미드 이미지
- 같은 영상의 해상도를 1/2씩 줄인 여러가지 버전으로 가지고 있는 것(다해상도)
- 특정 필터를 다양한 해상도의 영상에서 사용해야만 효과를 발휘할 수 있는 것이 있음
- 같은 영상의 해상도를 1/2씩 줄인 여러가지 버전으로 가지고 있는 것(다해상도)
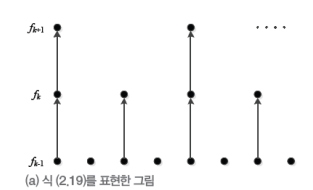
- 피라미드의 구축 연산
- 각 단계(피라미드의 한 층)별로 인접한 2개중 1개의 픽셀만 올리는 방법
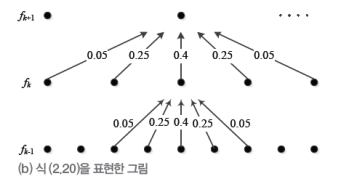
- 앞의 방법의 에일리어싱 효과를 개선(비율을 정해 다음 단계로 올려주는 방법
- 각 단계(피라미드의 한 층)별로 인접한 2개중 1개의 픽셀만 올리는 방법
- Burt&Adelson 방법
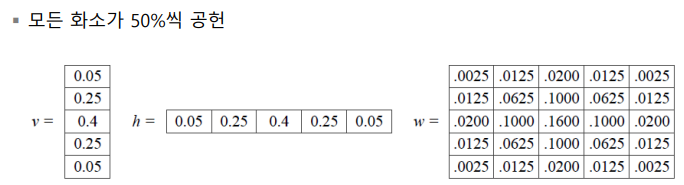
- 비행기 검출 크기가 3x3만큼 작다고 가정하면 영상의 크기가 그 정도로 작아져야 할 필요가 있음(영상이 커서 모든 구간에 필터를 적용한다해도 비행기의 일부분만 검출되기 떄문)

모폴로지
- 패턴을 원하는 형태로 변환하는 기법
- 이진 모폴로지
- 팽창 : 본인이 1이면 구조요소를 모두 1로 만듬
- 침식 : 구조요소가 모두 1이 아니면 본인을 0으로 만듬
- 열기 : 침식 후 팽창 계산
- 닫기 : 팽창 후 침식 계산
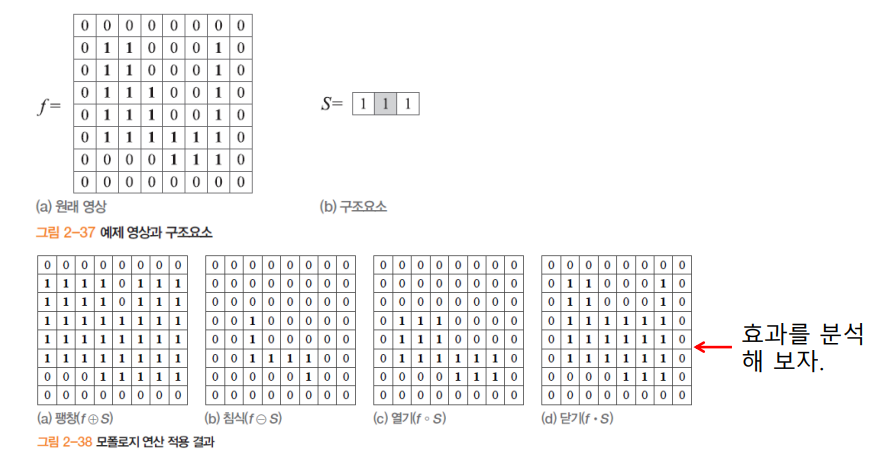
- 열기와 닫기는 팽창, 침식으로 인한 크기의 변화를 원래대로 돌려놓기 위해서 하는 것
- 침식으로 주변의 노이즈를 지우면 중앙의 원래 원하는 영상의 크기가 작아짐
- 그 후 팽창을 하면 노이즈 삭제는 유지하면서 중앙 영상의 크기를 복구함
- 닫기는 가운데 영상의 작은 구멍을 메꾸는데 사용