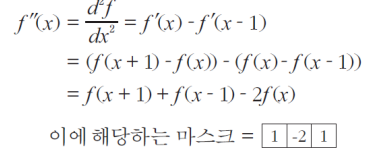엣지 검출
- 엣지의 활용
- 물체의 경계를 표시
- 매칭에 용이한 선분이나 곡선으로 변환
- 엣지의 한계
- 실종된 엣지(거짓 부정), 거짓 엣지(거짓 긍정) 발생
엣지 검출의 기초
원리
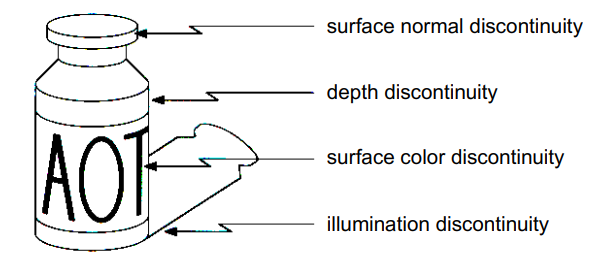
- surface normal discontinuity : 엣지로 어떤 물체인지 구분 가능
- depth discontinuity : 배경과 물체를 구분 가능함
- surface color discontinuity : 색 정보로도 엣지를 검출 가능
- illumination discontinuity : 조명, 그림자에 대한 정보도 검출 가능
명암, 걸러, 텍스처의 변화량을 측정하고 변화량이 큰 곳을 엣지로 검출
디지털 영상의 미분
- 연속 공간이 아닌 디지털 공산에서의 미분이 필요함

- 디지털 영상에서 가장 작은 변화량은 명암값 1이므로 델타의 최솟값은 1
- f(x+1) - f(x) : 바로 옆 픽셀과 본인 픽셀의 차이
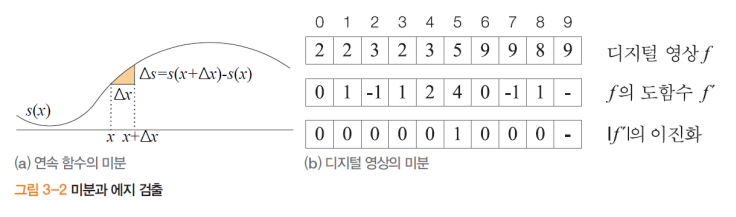
- [-1][1]의 필터로 구현 가능
에지 모델과 연산자
- 1차 도함수의 계단과 램프부분이 엣지라고 판단 가능(자연 영상에서는 램프 엣지가 주로 나타남)
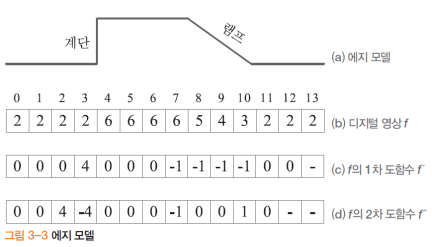
- 램프의 어느 부분을 엣지로 할지가 애매한 문제가 있음(2차 미분으로 해결)
- 2차 미분에서는 하나의 영역에 대해서 엣지가 2개씩 생김(2차 도함수의 4, -4, -1, 1이 해당)
- 2차 미분의 필터 : [1][-2][1]
램프 에지에서의 미분 반응
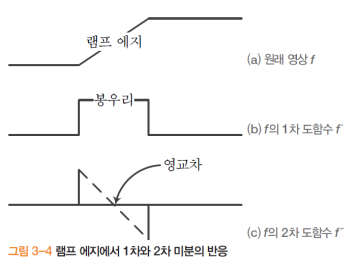
- 영교차 이론
- 2차 미분에서 한 영역에 2개의 엣지가 생기는 단점을 해결하는 방법
- 2개의 엣지의 가운데인 영교차에 해당하는 픽셀을 하나의 엣지로 판단

Characterizing edges
- 1차 미분의 극소 극대값이 엣지라고 판단 가능
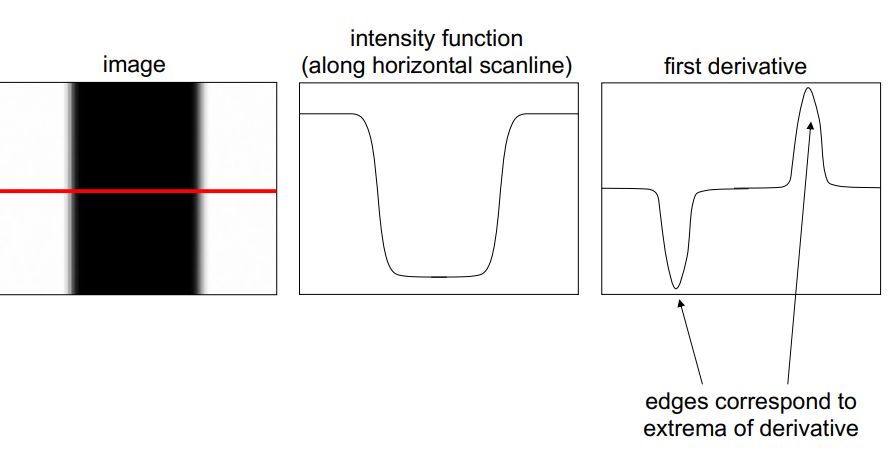
- 빨간선에 대해서의 명암값과 1차 미분 값
- 그라데이션 형태로 이미지가 존재하기 떄문에 곡선형태로 명암, 1차미분 그래프가 나옴
Effects of noise
- 잡음이 있는 영상에서는 가우시안 필터로 이미지를 편집후 도함수를 구함
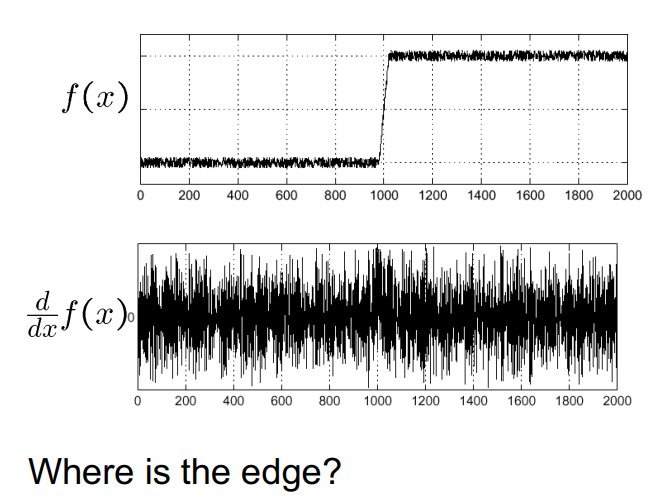
- 영상에 잡음이 있는 경우의 1차 미분(엣지를 구하기 힘듬)
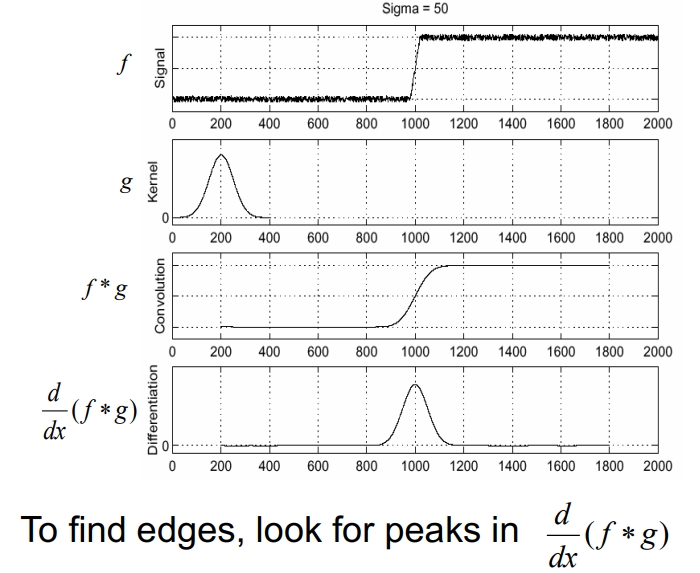
- 가우시안 필터 g를 활용한 방법
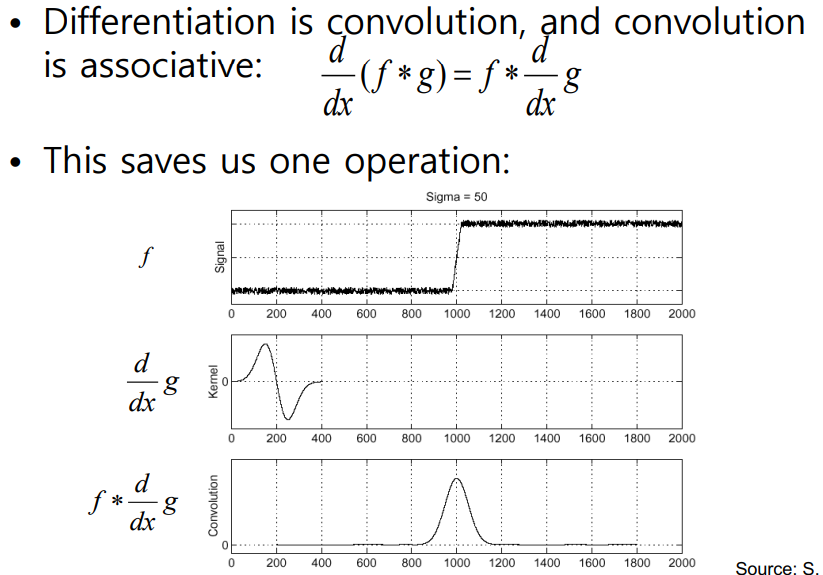
- 연산 횟수를 줄이기 위해 가우시안 필터를 먼저 미분한후 적용하면 연산이 줄어듬
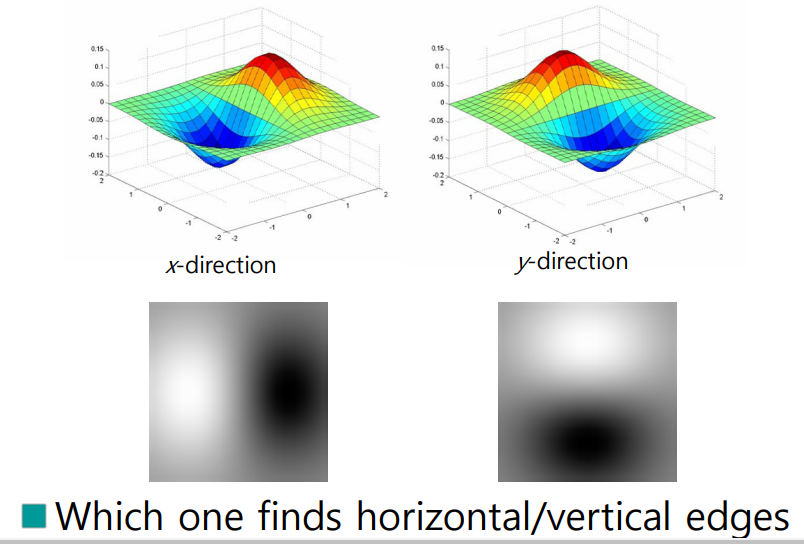
- x, y방향의 가우시안 필터를 통한 수직, 수평 엣지를 판별
- 현실에서는 잡음 때문에 스무딩 필요 : 델타 x의 값을 2로 확장

- 가로방향의 그레디언트를 구하는 필터는 세로(수직) 방향의 엣지를 구함 그레디언트와 엣지는 수직관계일수 밖에 없음
- 대각선, 가로, 세로 엣지 판결 필터, 소벨은 본인축의 값을 더 강조하는 효과도 있음
엣지 강도와 방향
- 그레이디언트 : 어느 방향으로 변하는지와 변하는 강도를 계산 가능(계단 엣지의 경우 강도가 강한 경우임)
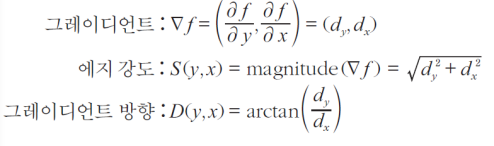
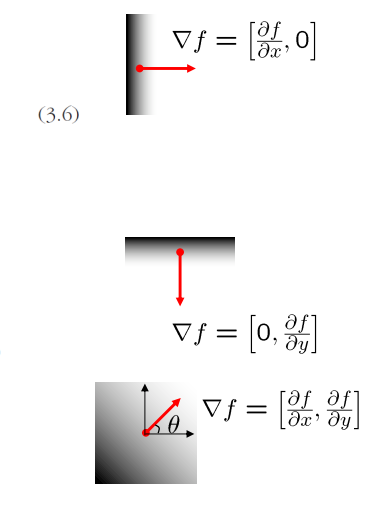
- 그레이디언트는 벡터이기 때문에 방향과 크기를 모두 계산 가능
- x,y의 변화 방향에 따라 변화량이 0인 경우와 둘다 변하는 경우
- 소벨 필터를 씌워 x,y로의 변화(dy, dx)를 구함
- -4, 2가 나오고 각각의 제곱에 루트를 씌우면 강도
- 아크탄젠트 (dy/dx) : 방향

- 짙게 표현된곳과 옅은 곳으로 명암 차이의 강도를 구분 가능, dx, dy로는 방향을 판단 가능
영교차 이론
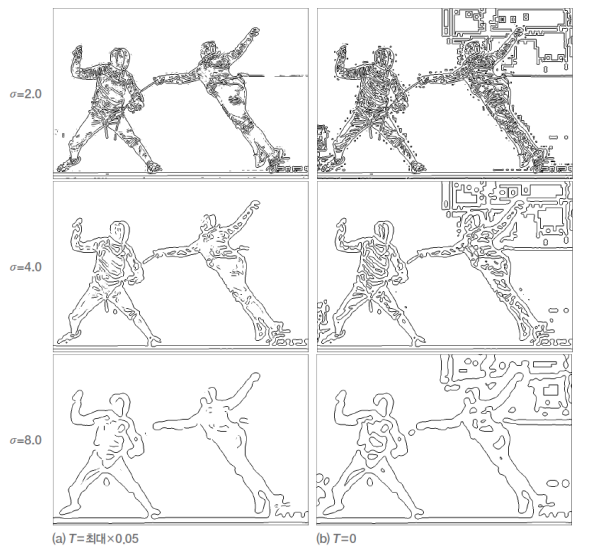
가우시안과 다중 스케일 효과
- 미분은 잡음을 증폭시키므로 스무딩 적용이 중요
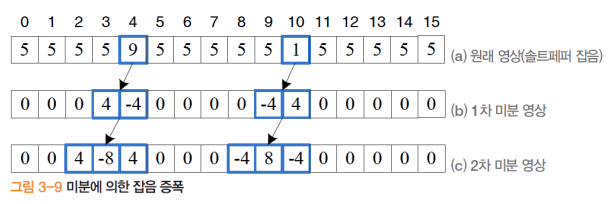
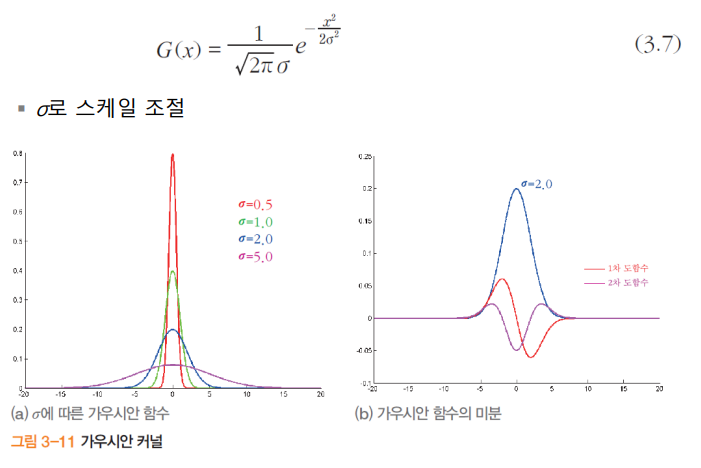
- 가우시안 필터의 시그마 값의 조정으로 다른 효과를 얻을 수 있음
- 가우시안의 시그마 값의 변화에 따라 가우시안 함수의 미분값도 여러가지로 달라짐
- 2차원 가우시안
- 2차원에서 가우시안 필터의 크기는 시그마의 크기와 비례함
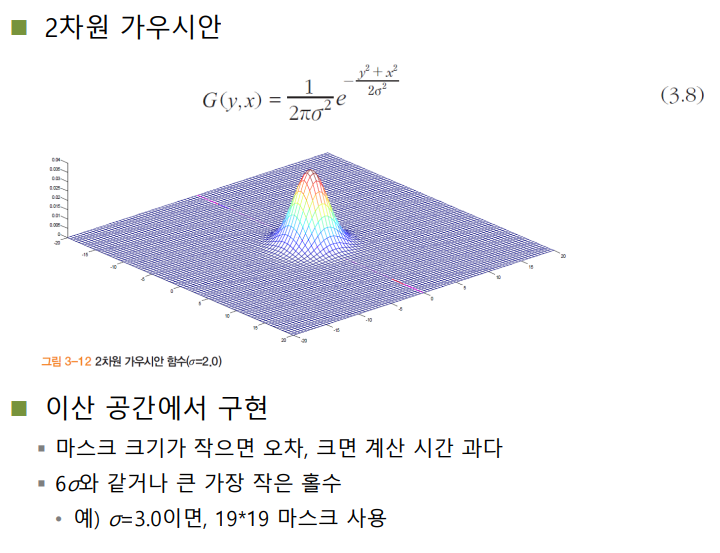
- 필터가 크면 스무딩 효과가 크지만 시간이 오래 걸림
Log 필터
- 엣지 검출 과정
- 시그마 크기의 가우시안으로 영상을 스무딩
- 2차 도함수를 구함(이때 라플라시안 사용)
- 2차 도함수의 영교차를 엣지로 설정
- 라플라시안
- 샤프닝 필터의 모양과 반대임

- 영상에 가우시안 g를 적용하고 다시 라플라시안을 적용하는 과정에서 계산 시간 과다와 오류가 누적 됨
- 로그 오브 가우시안 필터를 활용하여 한 단계로 처리 가능
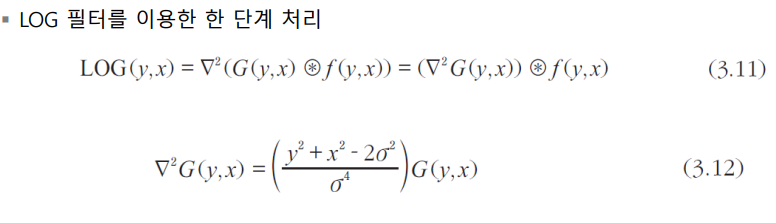
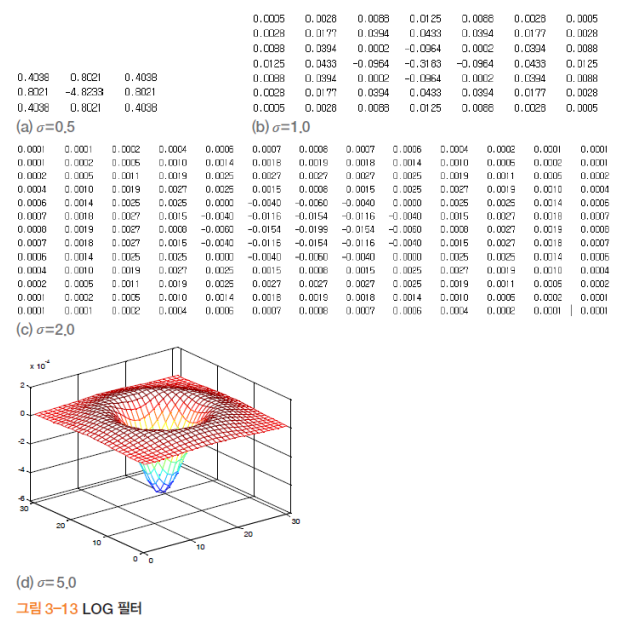
- Log 필터
- 시그마 값에 따른 Log필터 적용 결과
컬러 엣지
- RGB채널에 독립적으로 적용 후 결합
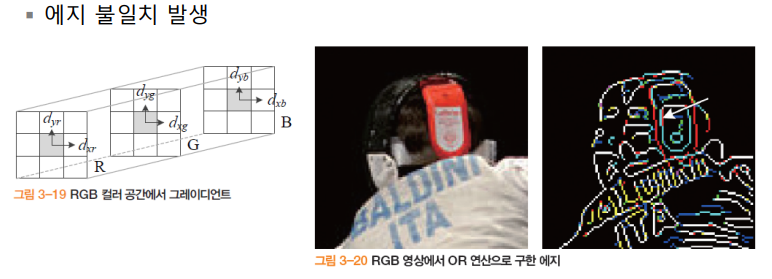
- 색깔별로 기존의 엣지 검출 방법을 적용하고 원하는대로 교집합이나 합집합으로 엣지를 검출함