개인스터디
통계학 기초 3주차
A/B 검정
두 그룹(A, B)의 효과를 비교!
- 두 그룹을 비교하여 어떤 버전이 더 효과적인지 판단하는 방법
- 사용자의 반응(전환율, 클릭률, 매출 등)을 비교하여 의사결정
예시
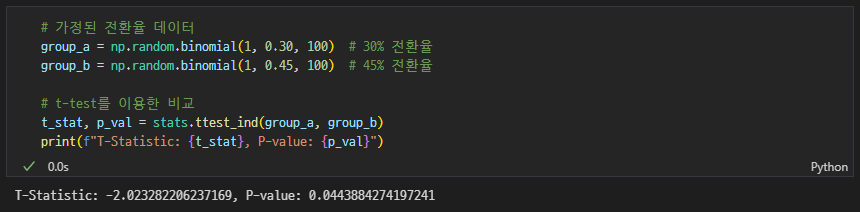
p-value = 0.044 < 0.05
→ A그룹과 B그룹의 전환율에는 통계적으로 유의미한 차이가 있다
→ B그룹 채택
가설검정
데이터가 가설을 지지하는지 확인
-
표본 데이터를 이용해 모집단에 대한 가설(H0 vs H1)을 검증
- 귀무가설(H0): 차이가 없다
- 대립가설(H1): 차이가 있다
-
일반적으로 p값 < 0.05이면 귀무가설 기각 → 통계적으로 유의미함
예시
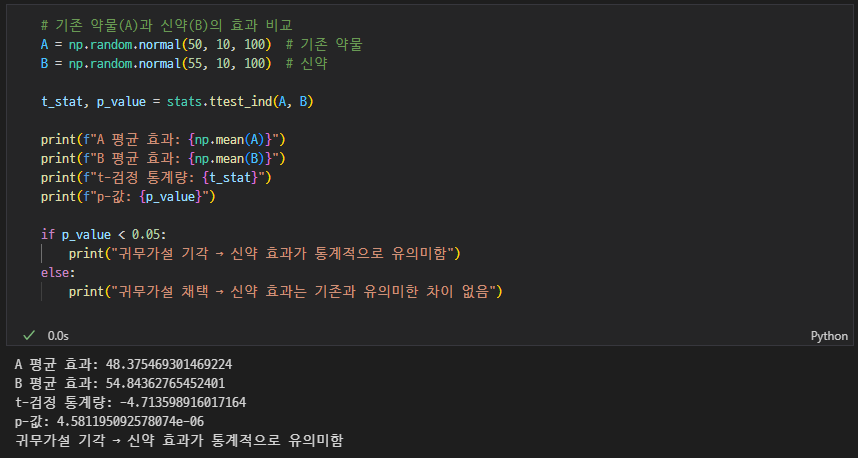
t검정
가설검정에서 평균 차이를 비교할 때 자주 사용하는 방법
- 독립표본 t검정: 서로 다른 두 그룹 비교
- 대응표본 t검정: 같은 그룹의 전후 비교 (예: 다이어트 전후)
다중검정
여러 가설을 동시에 검정할 때 생기는 오류 주의
-
유의수준을 조정하지 않으면 1종 오류 발생 확률 증가
-
하나의 검정에서 제1종 오류가 발생하지 않을 확률
-
m개의 독립된 검정에서 모두 오류 없이 끝날 확률:
-
따라서 하나 이상의 제1종 오류가 발생할 확률(전체 오류율)
-
α = 0.05, m = 10일 경우:
→ 약 40.1% 확률로 적어도 하나의 오류 발생 가능
-
-
보정 기법 필요
- 본페로니 보정이 대표적
→ 유의수준 α를 비교 횟수만큼 나누어 오류율 제어
→ ex) α = 0.05, m = 3 → 보정된 α = 0.0167
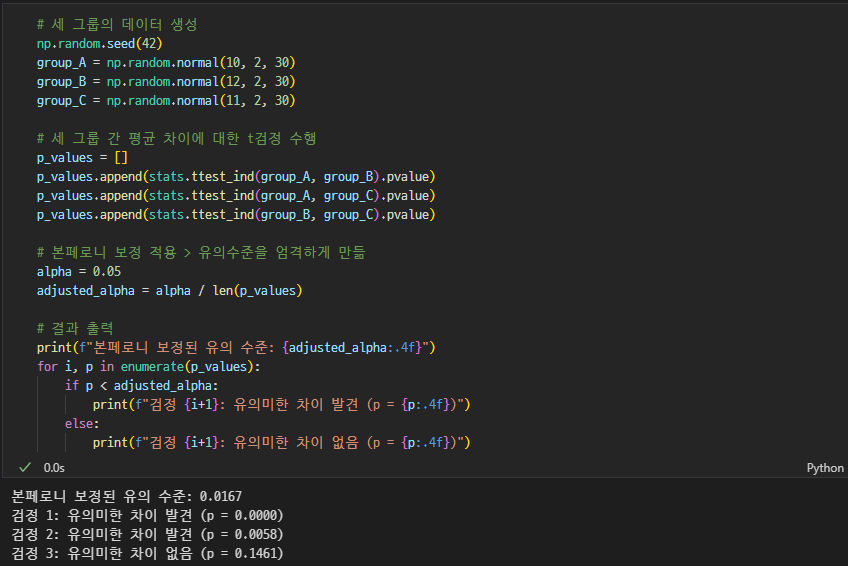
- 본페로니 보정이 대표적
카이제곱검정
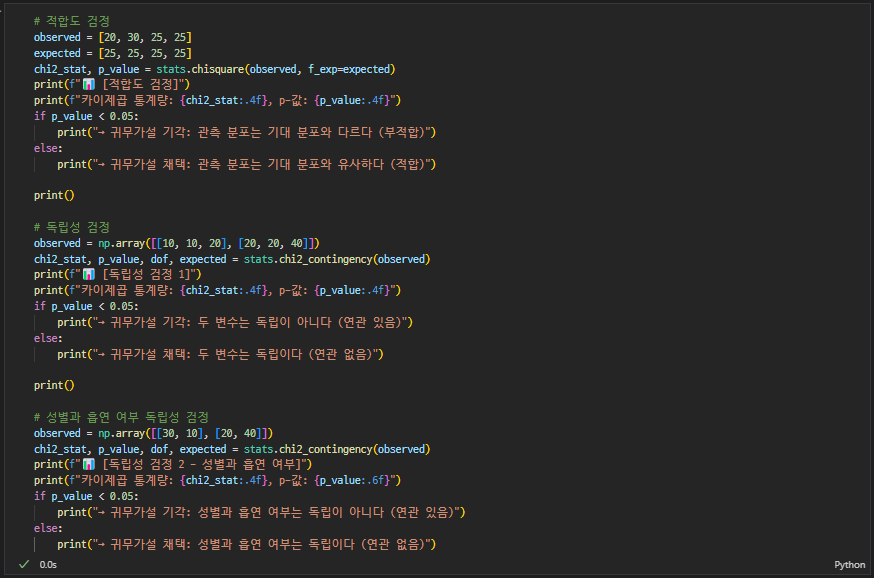
범주형 데이터 분석에 사용
- 적합도 검정: 관찰 분포 vs 기대 분포 비교
- p값이 높으면 데이터 = 귀무가설 > 적합
- p값이 낮으면 데이터 != 귀무가설 > 부적합
- 독립성 검정: 두 범주형 변수 간의 독립 여부 판단
- p값이 높으면 두 변수간 연관성 X > 독립성 O
- p값이 낮으면 두 변수간 연관성 O > 독립성 X
⚠️ 통계량과 p값을 비교하는 게 아니라, p값을 보고 판단하는 것

제 1종 오류 vs 제 2종 오류
| 구분 | 정의 | 예시 |
|---|---|---|
| 제 1종 오류 (α) | H0가 참인데 기각 | 효과 없음 → 효과 있다고 판단 |
| 제 2종 오류 (β) | H0가 거짓인데 채택 | 효과 있음 → 효과 없다고 판단 |
(+) 통계복습
세션 1~3회차 + 강의 1~3주차 관련 내용
1-3. 아래 중 정규분포(Normal Distribution)의 특징이 아닌 것은?
A. 평균을 중심으로 좌우 대칭이다.
B. 종 모양의 곡선을 따른다.
C. 중심 극한 정리에 의해 항상 정규분포를 따른다. ✅
D. 평균과 중앙값, 최빈값이 모두 같다. ❌
C. '항상' 정규분포를 따르는 것은 아님
표본의 크기가 충분이 클 때 적용
D. 정규분포 특징 > 평균 = 중앙값 = 최빈값
1-6. 정규분포는 모든 확률변수가 따르는 보편적인 분포이다. (O/X) ❌
이것도 위 문제랑 같은 맥락으로 오답
모든 데이터가 정규분포를 따르지는 않음
2-5. 유의수준은 제1종 오류의 확률이다? (O/X) ⭕
귀무가설이 실제로는 참인데 기각하는 오류의 확률
허용 가능한 오류 수준을 정하는 것
2-6. p-value는 대립가설이 참일 확률이다? (O/X) ❌
p-value는 귀무가설이 참이라는 가정 하에, 관측된 결과만큼 극단적인 결과가 나올 확률이므로
대립가설의 확률을 직접적으로 의미하지 않음
2-7. 신뢰구간 계산 시 필요한 요소 3가지
표본평균(중심통계량), 표본오차, 신뢰수준(z/t값)
3-7. A/B 테스트 가설 설정
귀무가설 : A와 B 사이에 차이가 없다
대립가설 : A와 B 사이에 차이가 있다
3-8. t 검정은 언제 쓸까?
모표준편차를 모를때 + 표본이 작을때 사용
3-9. 기대도수란?
귀무가설이 참일때, 각 범주에 기대되는 관측값
관측값과 기대도수의 차이가 크면 귀무가설을 기각할 근거가 됨
코드카타
SQL - 저자 별 카테고리 별 매출액 집계하기
SQL - 대여 횟수가 많은 자동차들의 월별 대여횟수 구하기
일기
- SQL
코드카타 68-69✅ - 통계
세션 1-3회차 복습✅기초강의 1-2주차 복습✅기초강의 3주차✅기초강의 4주차❌ - 수준별학습
1-2회차 이론복습✅
원대한 계획을 잡긴 했으나 ... ^ ^ 숙취이슈로 크게 집중하지 못했다
머신러닝 강의도 지급됐겠다 얼른 통계 강의는 끝내놔야 할 것 같아서 오늘 4주차까지 듣고 싶었는데 하하 누굴 탓하겠어
내일 시간 잘 쪼개서 열심히 집중 해봐야겠다
아마 스탠다드 중간중간 스탠다드 강의때문에 시간이 여유롭진 않겠지만 어케든 하면 할 수 있겠지
이번주도 파이팅해보자 아자자
