Graph
- 정점(node, vertex)과 간선(edge)로 이루어진 자료구조
• 간선은 가중치(weight)를 가질 수 있음 - 방향 그래프와 무방향 그래프로 나누어짐
• 무방향 그래프 종류
1) 연결 그래프 : 모든 정점간 경로가 존재할 때
2) 비연결 그래프 : 모든 정점간 경로가 존재하지 않을 때 - 주요 용어
• 차수(degree) : 무방향 그래프에서 한 정점에 인접한 정점 수(간선 수)
• 진입 차수(in-degree) : 방향 그래프에서 내부로 향하는 간선 수
• 진출 차수(out-degree) : 방향 그래프에서 외부로 향하는 간선 수
• 사이클(cycle) : 경로의 시작 정점과 종료 정점이 동일한 것 - 그래프는 인접리스트와 인접행렬로 구현됨
인접행렬
- 보통 2차원 행렬 형태로 나타냄
- 행과 열에 해당하는 인덱스 칸에 값이 적힌 경우, 해당 값이 간선의 가중치가 된다
장점
- 임의의 두 정점 사이의 간선의 존재 유무를 한번에 확인할 수 있다
- 정점 사이 간선의 가중치를 빠르게 파악할 수 있다
단점
- 그래프 내에 존재하는 간선들의 수를 계산하는 것이 힘들다
- N개의 노드를 표현하기 위해서는 N^2개의 공간이 필요하다
- 원하는 노드가 간접적으로 연결되어있는지 확인하기 위해서는 모든 노드를 순회해야한다
인접 리스트
- 해당 노드에 연견된 간선이나 노드의 정보를 리스트 형태로 나타낸다.
장점
- 임의의 정점과 인접한 노드를 쉽게 찾을 수 있다
- 임의의 정점과 연결된 간선의 갯수를 쉽게 파악할 수 있다
단점
- 임의의 두 정점이 연결되어 있는지 확인하기 위해서는 양쪽 노드의 리스트를 모두 탐색해야 한다
Binary Tree
- 각 노드가 최대 두개의 자식을 가지는 트리
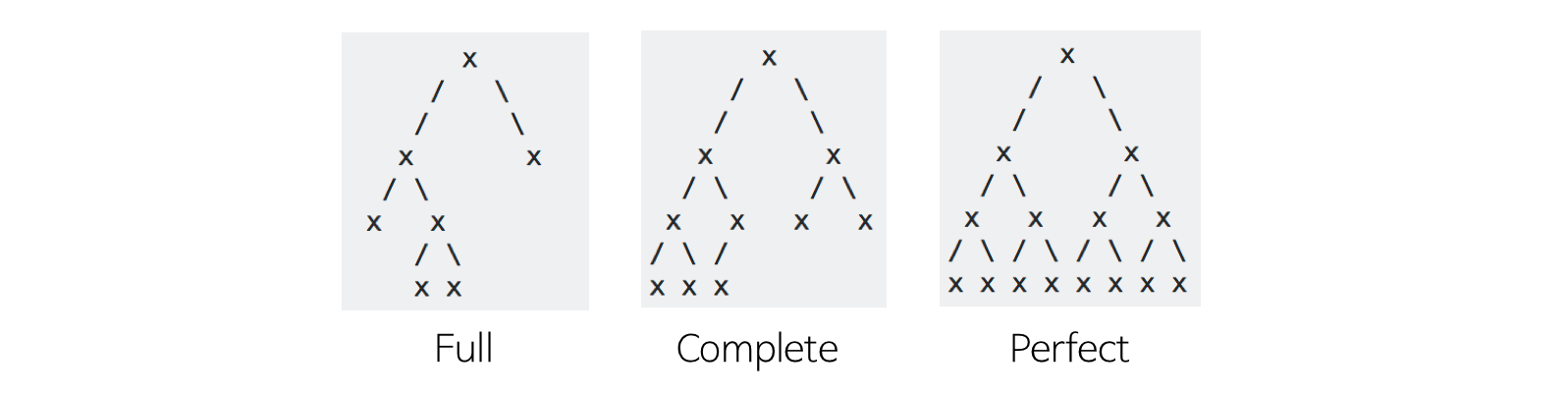
전 이진트리 (Full Binary Tree)
- 모든 노드가 자식을 0개 or 2개 가지는 트리
완전 이진트리 (Complete Binary Tree)
- 노드가 꽉 차있으며, 마지막 레벨에서는 왼쪽으로 차 있는 트리
• 왼쪽 노드부터 순서대로 채운 트리
• 루트노드부터 시작해서 왼쪽 자식 노드 -> 오른쪽 자식 노드 순으로 추가함 - 배열을 통해 표현 가능
포화 이진트리 (Perfect Binary Tree)
- 전 이진트리 + 완전 이진트리
- 모든 레벨에서 노드가 가득 차 있는 트리
정렬 이진 트리
이진 탐색 트리 (Binary Search Tree)
- 좌-우 노드가 부모를 기준으로 정렬된 트리
• 왼쪽노드는 부모보다 작고, 오른쪽 노드는 부모보다 크다
• 트리에서 가장 왼쪽에 위치한 노드가 가장 작은값을 가진다 - 중복 키값을 허용하지 않음
- 탐색시 성능
• 평균 : O(logN) == 높이
• 최악(불균형일 경우) : O(N)