Heap
- 최솟값 및 최대값을 최대한 빠르게 찾아내기 위해 특별히 고안된 자료 구조, 완전 이진트리를 기본으로 하고 있으며(마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리의 형태), 그 목적에 걸맞게 두개의 타입으로 나눈다. -> 사용이유는 루트의 값만 바로 가져오면 되기에 O(1) 시간 복잡도 만으로 최대값 혹은 최소값을 찾을 수 있다.
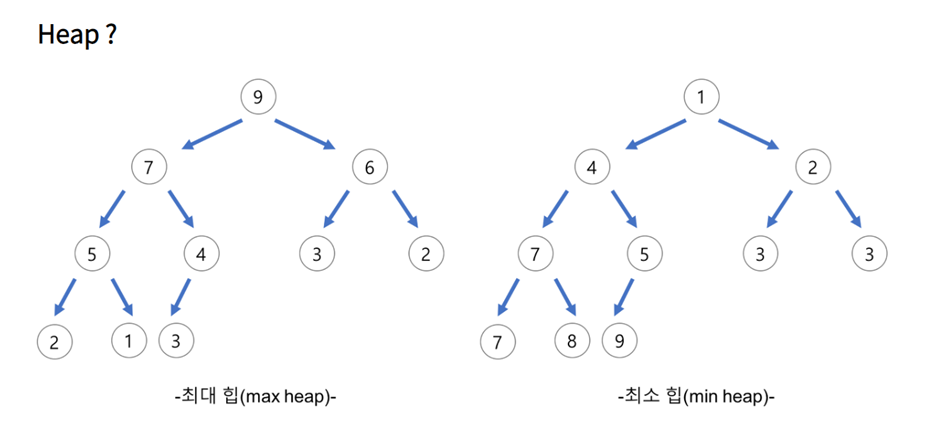
1) Max-Heap : Max-Heap에서 root노드의 key는 무조건 해당 노드의 자식 노드들의 key보다 크거나 같다 Max-heap 트리에서 자식 노드에 딸린 트리 하나 하나가 모두 Max-Heap의 조건을 만족함
2) Min-heap : Min-heap 에서는 반대로 root 노드의 키값이 모든 자식들의 키 보다 작거나 같고 , 재귀적으로 자식 트리들 하나하나 모두 해당 조건을 만족
Trie
- (retrieval Tree) 문자열들을 트리 구조로 저장하여 O(log n) 속도로 빠르게 문자열을 탐색 주로 알고리즘 문제에서는 ‘접두어’/’접미어’ 등의 키워드가 나오는 문제에 사용
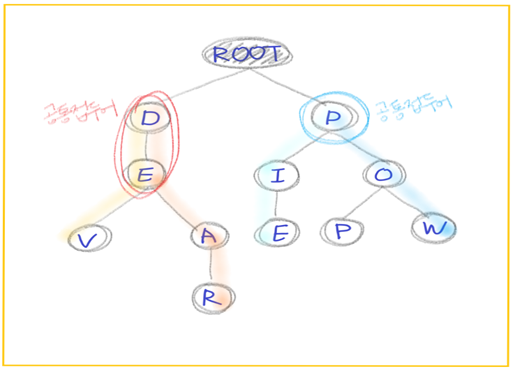
Trie 자료구조 형태
- 각 노드는 <key,value> 맵을 가지고 있고, Key는 하나의 알파벳,Value는 그 Key에 해당하는 자식 노드가 된다. 또한 루트 노드를 제외한 노드의 자손들은 해당 노드와 공통 접두어를 가진다.
AVL Tree
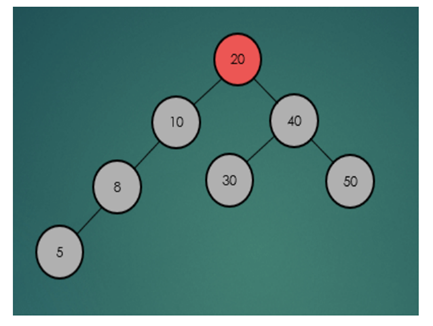
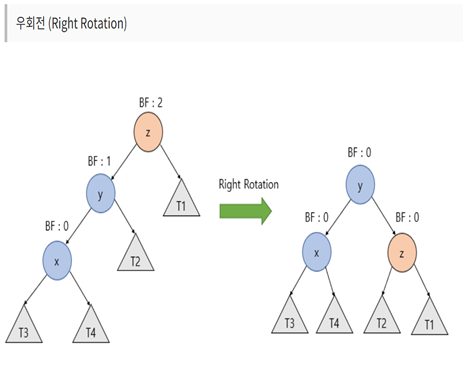
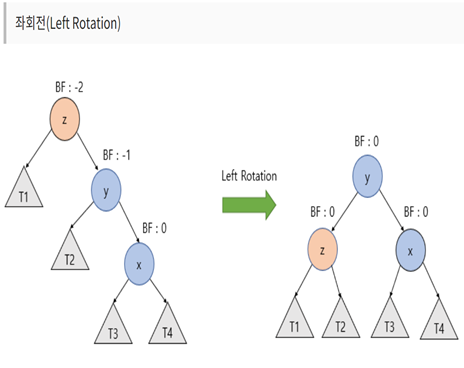
- 트리 높이의 균형을 유지하는 이진탐색트리, 엄격하게 균형을 유지하기 때문에 Red-black 트리보다 더 빠른 성능을 가지지만 더 많은 작업을 수행해야만 한다. 왼쪽 자식노드는 부모 노드보다 작고,오른쪽 자식노드는 크다. 탐색은 이진트리와 동일 높이의 균형을 맞추기 위해 회전을 한다. 균형도가 2미만 일 경우 균형트리이다.
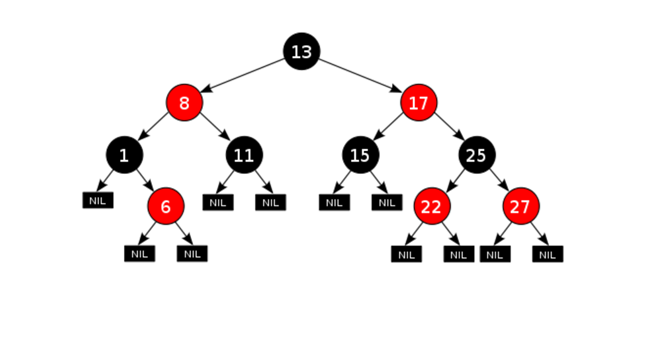
Red-Black Tree
-
자가 균형 이진 탐색 트리
-
모든 노드들이 블랙/레드의 색을 가지고, 루트 노드와 마지막 노드(리프 노드)는 블랙을 가진다. 레드 노드는 연속적으로 나올 수 없고(자식 노드들은 모두 검정),모든 리프노드에서 루트노드까지 가는 경로의 블랙노드의 개수는 모두 같다.
-
모든 새로운 노드는 빨간색 색상으로 가진채로 삽입 되어야한다. 추후 레드_블랙 트리의 조건에 맞게 변경
삽입 절차
- 트리가 비었는지 확인 ->비었다면 ,검은색 루트 노드 / 비어있지 않다면, 빨간색 리프 노드
2.새 노드의 부모가 검은색이라면,연산을 마침 /빨간색이라면, 새 노드의 부모의 형제를 확인 - 새 노드의 부모의 형제가 검은색 혹은 Null이면, 적절한 회전과 재색칠을 한다.
/새 노드의 부모의 형제가 빨간색이면,재색칠을 한다.