정렬 알고리즘
1. 선택 정렬
- 현재 배열중 최소(최대) 값을 찾아 그 값을 맨 앞(뒤) 자리 값과 교체하고 나머지 배열중 다시 최소(최대)값을 찾아 그 다음 맨 앞(뒤)자리 값과 교체를 반복함
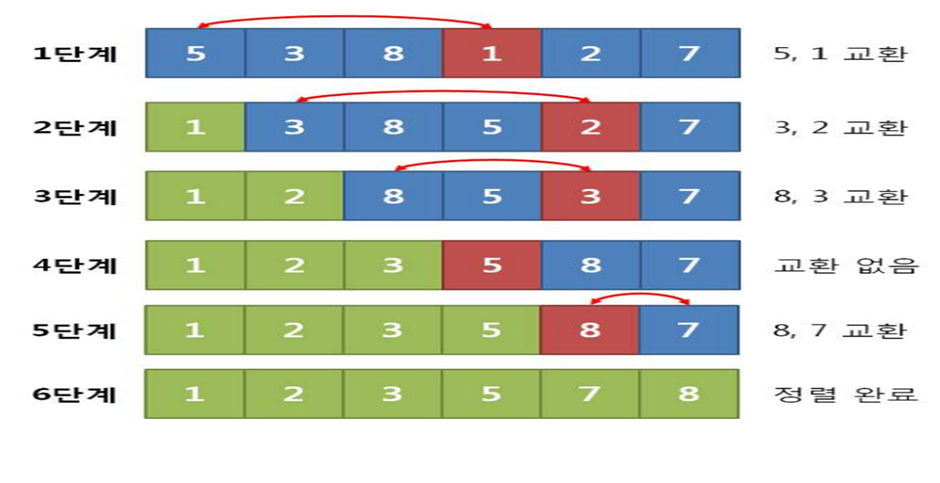
2. 거품 정렬
- 서로 인접한 두 원소를 검사하여 정렬하기를 반복, 구현이 매우 간단하지만 교환 작업이 복잡하고 효율이 좋지 않음
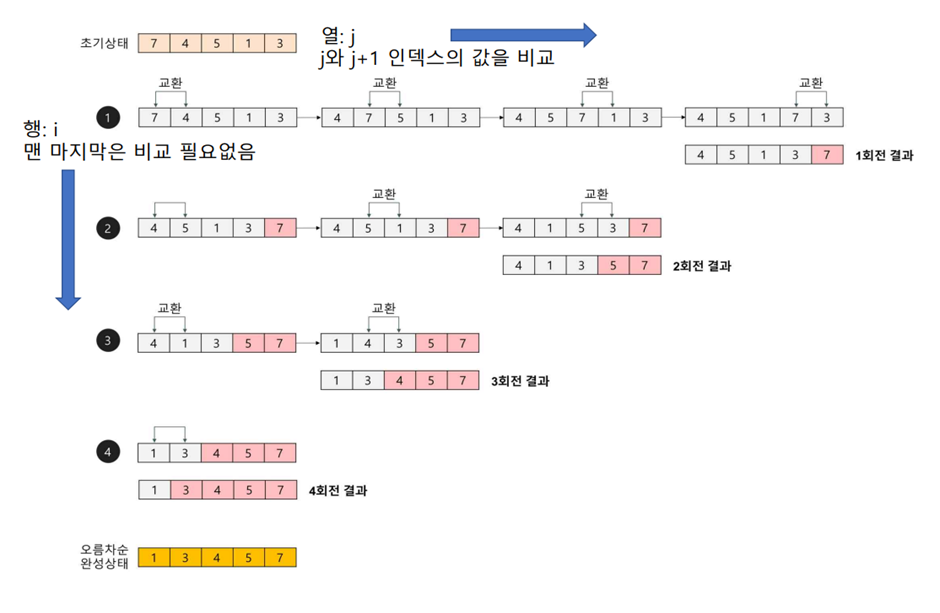
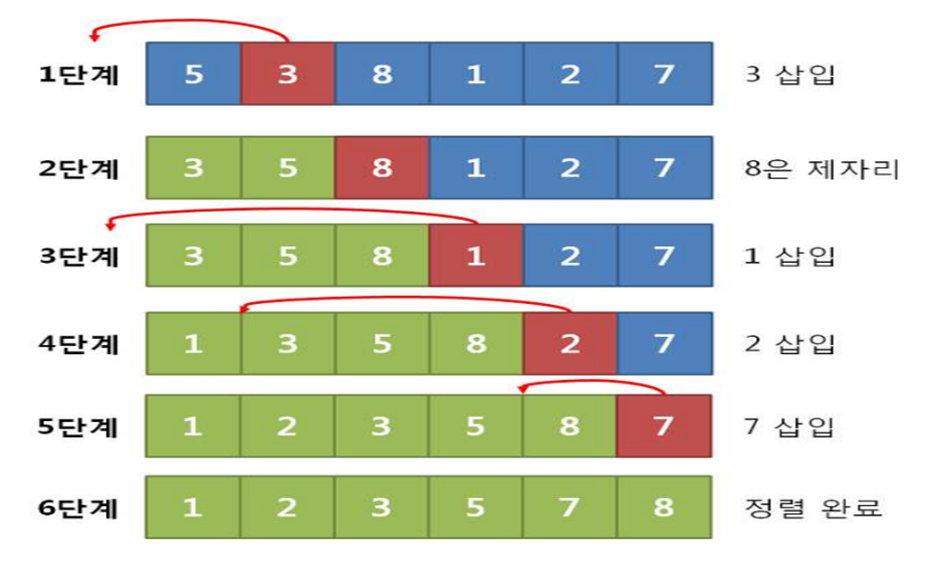
3. 삽입 정렬
- 새로운 수를 기존 정렬된 수 사이의 올바른 자리를 찾아 삽입함으로써 정렬 유지
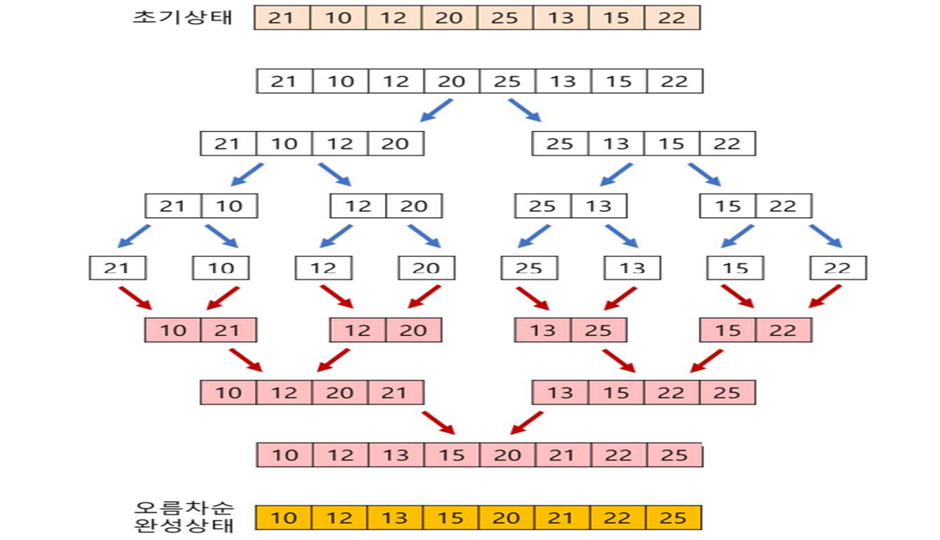
4. 병합 정렬
- 입력된 배열을 같은 크기의 부분 배열 2개로 분할, 더 이상 분할 할 수 없을 때까지 분할, 부분 배열을 정렬하고 부분배열을 병합하면서 정렬 반복. 분할 정복 방법을 이용한다는 점에서 퀵정렬과 유사
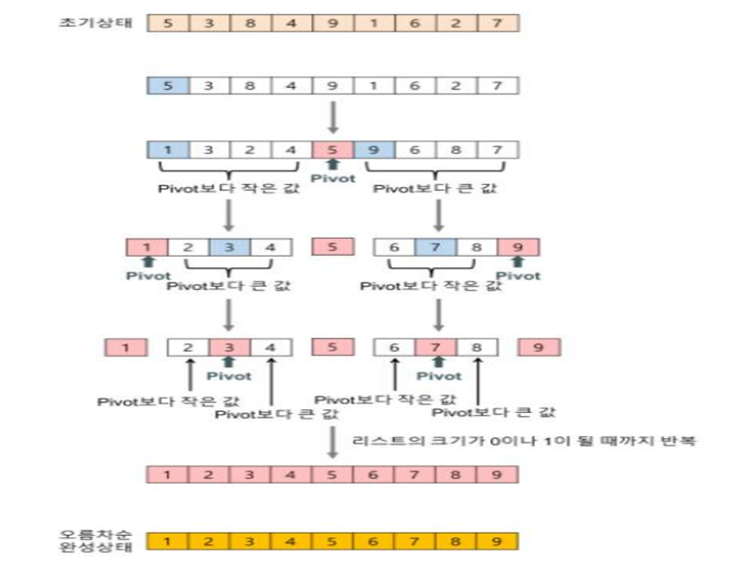
5. 퀵 정렬
- 분할 정복 방법-> 문제를 작은 문제로 분리하고 각각을 해결한 뒤 결과를 모아서 원래의 문제를 해결하는 전략,분할 정복 문제는 대개 재귀함수로 구현하는 것이 효과적
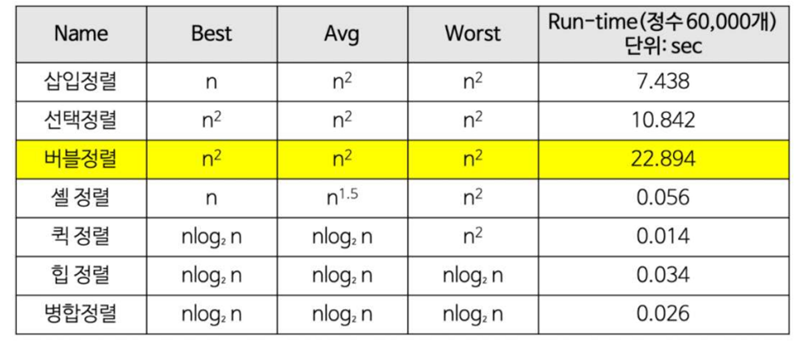
정렬 알고리즘별 시간복잡도 비교
이분탐색
- 정렬된 배열 또는 리스트에 적합한 고속 탐색법
-> 배열의 중앙에 있는 값을 조사하여 찾고자 하는 값이 왼쪽 또는 오른쪽 부분에 있는지 알아내어 범위를 반으로 줄인 후 반복(주로 고정된 데이터에 대한 탐색에 적합)

Mid 값(0+n-1)/2을 구하고자 하는 값과 비교 후 key==mid가 될 때 까지 반복
동적계획법
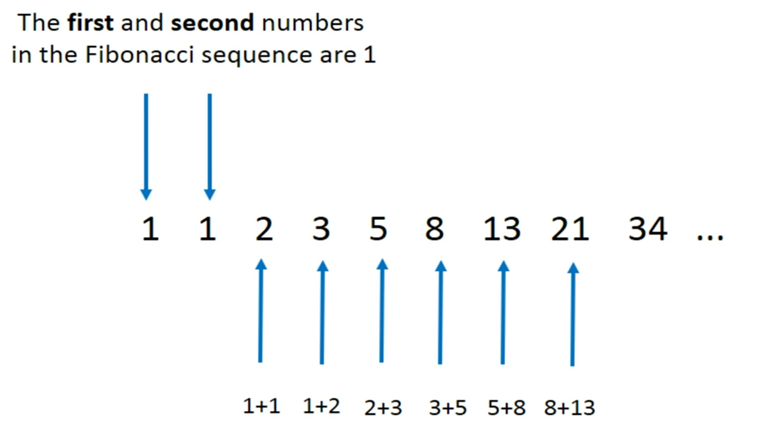
- 특정 범위까지의 최적해(상위 문제)를 구하기위해 다른 범위까지의 최적해(하위 문제)를 이용하여 효율적으로 해를 구하는 알고리즘 ex)피보나치 수열
-> Top-Down : 큰 문제를 작은 문제로 나누고 작은 문제를 풀어 재귀호출
-> Bottom-Up : 문제 크기가 작은 문제부터 차례대로 쓰고 크기를 조금씩 크게 만들면서 큰 문제의 답을 구함(반복문)
최단경로
- 특정 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 계산(다익스트라 최단 경로 알고리즘) 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정 반복
-> 출발 노드 설정
-> 최단 거리 테이블 초기화
-> 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드 선택
-> 해당 노드를 거쳐 다른 노드로 가는 비용 계산하여 최단 거리 테이블 갱신 후 반복
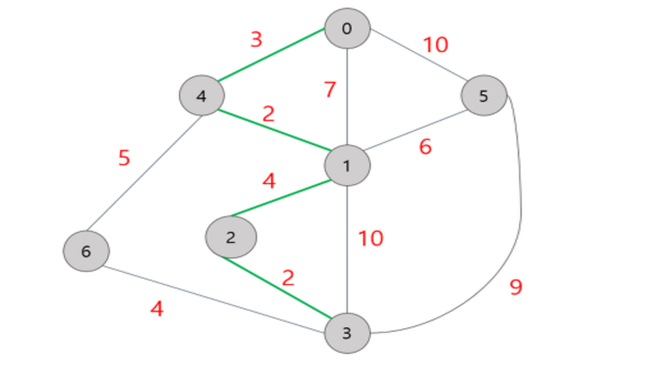
최소비용
- 트리를 구성하는 간선들의 가중치를 합한 값이 최소가 되는 신장 트리(크루스칼,프림)
프림
- 가중치가 있는 무방향 그래프의 최소 비용 신장 트리를 찾는 알고리즘
-> 그래프에서 시작 정점 선택
-> 선택한 정점에 부속된 모든 간선 중 가중치가 가장 작은 간선 연결하여 트리 확장
-> 이전에 선택한 정점과 새로 확장된 정점에 부속된 모든 간선 중 가중치가 가장 작은 간선 삽입(사이클을 형성하지 않는 가장 작은 간선 선택) (-> 반복)
-> 그래프에 n-1개의 간선을 삽입할 때까지 반복
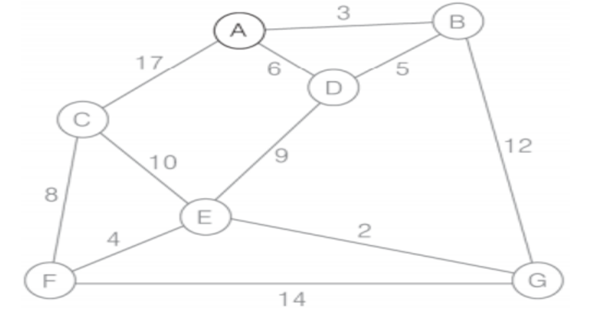
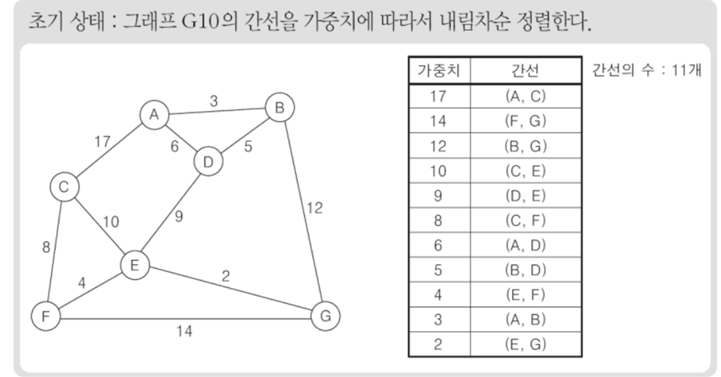
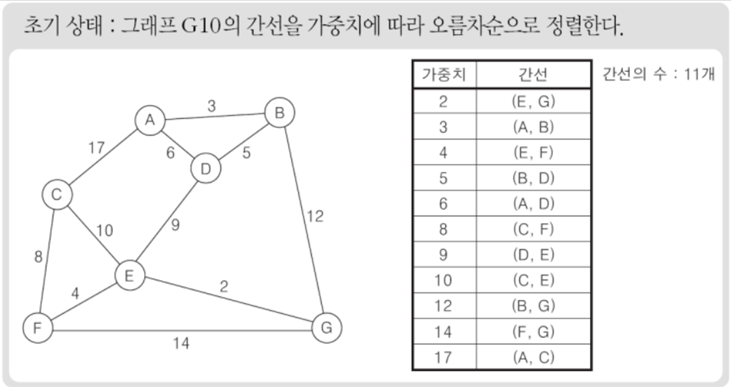
크루스칼 : 최소 비용 신장 부분 트리 찾는 알고리즘
-> 모든 간선을 가중치에 따라 내림차순 or 오름차순으로 정리
-> 가중치가 가장 높은 간선부터 제거 or 가장 낮은 간선부터 삽입(정점을 그래프에서 분리시키는 간선은 제거불가능 -> 그다음으로 가중치 높은 간선 선택)
-> N-1개의 간선만 남을 때 까지 반복