편집거리 알고리즘(Edit distance)?

편집 거리 알고리즘은 주어진 두 문자열 사이의 유사도를 판단하는 알고리즘이다.
이때 사용할 수 있는 연산은 다음 3가지 이다.

• 삽입(insert)
• 삭제(remove)
• 수정(modify)
  
  
  즉, 문자열 s1, s2가 주어졌을 때 위 3가지 연산을 사용해서 s1을 s2로 바꾸기 위해 사용한 연산의 횟수를 구하는 알고리즘이다.

연산을 살펴보자!

삽입(insert)

주어진 문자열이 아래와 같을 경우,
s1 : ab
s2 : abc
✅ s1의 맨 끝에 c를 삽입(insert)해서 s2로 바꿀 수 있다.

삭제(remove)

주어진 문자열이 아래와 같을 경우,
s1 : wxyz
s2 : xy
✅ s1에서 w와 z를 삭제(remove)해서 s2로 바꿀 수 있다.

수정(modify)

주어진 문자열이 아래와 같을 경우,
s1 : chiduen
s2 : chicken
✅ s1에서 d와 u를 c와 k로 수정(modify)해서 s2로 바꿀 수 있다.

구현은 어떻게?

편집거리 알고리즘은 Dynamic Programming, 이하 DP로 구현할 수 있다.

예시

주어진 문자열이 아래와 같을 때, 그림으로 살펴보자
s1 : abcdab
s2 : acbdcf

과정 0

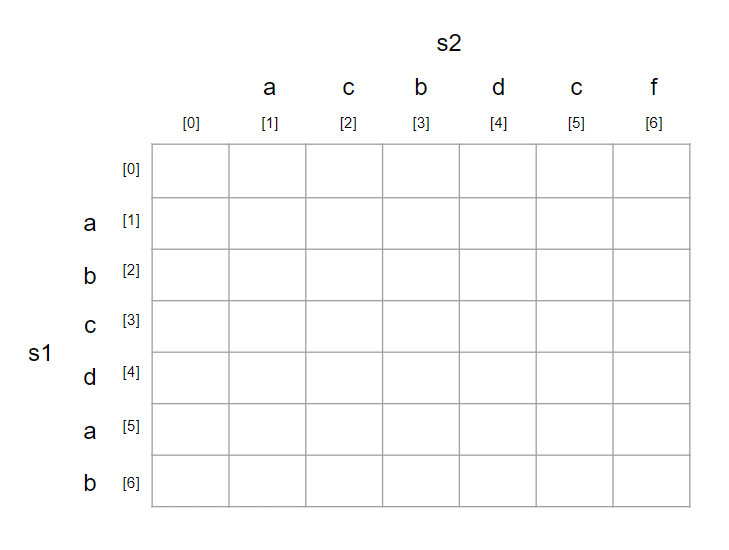
초기 표의 상태는 다음과 같다.
s1은 행으로, s2는 열로 표시한다.

과정 2

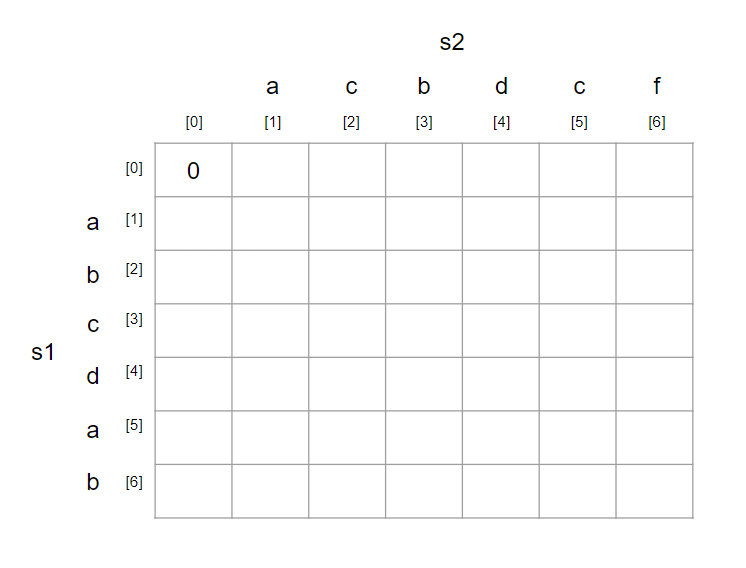
위의 표에서 (0, 0)은 문자가 없는 빈 문자열을 의미한다.
(0, 0)은 0으로 초기화해준다.

과정 3

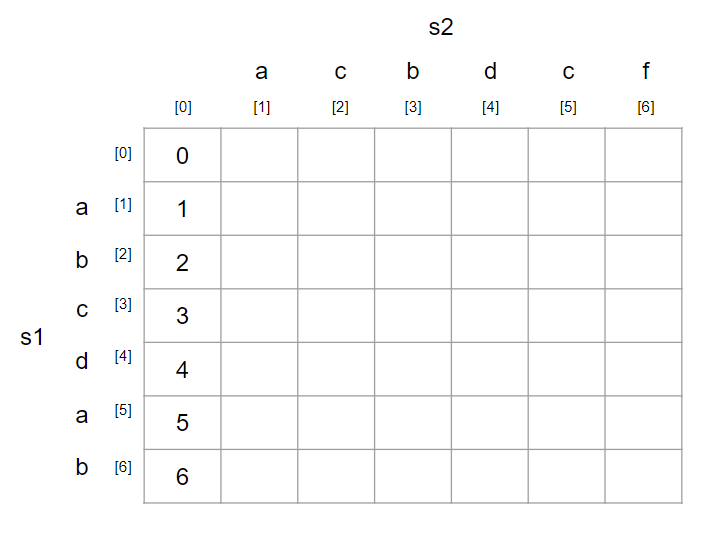
0번째 열은 s1 $\rightarrow$ 빈 문자열로 바꿀 때 필요한 연산의 횟수를 의미한다.
즉, 삭제(remove)연산을 몇 번 해야하는지를 채우면 된다.

과정 4

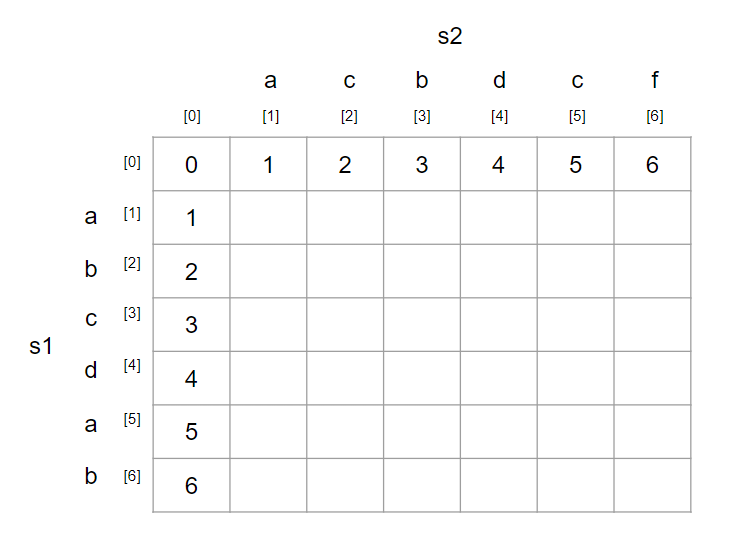
0번째 행은 빈 문자열 $\rightarrow$ s2로 바꿀 때 필요한 연산의 횟수를 의미한다.
즉, 삽입(insert)연산을 몇 번 해야하는지를 채우면 된다.
이렇게 해서 처음에 수행해야 하는 DP 테이블의 초기화는 끝이다.

알고리즘 플로우

1. s1의 i번째 문자와 s2의 j번째 문자를 비교한다.
   (편의상 s1[row - 1], s2[col - 1]로 칭하겠다.)
2. s1[row - 1] == s2[col - 1] 인 경우
3. s1[row - 1] != s2[col - 1 인 경우

먼저 s1[row - 1] == s2[col - 1]인 경우를 살펴보자
비교하는 두 문자가 같은 경우, 별도의 연산을 수행할 필요가 없기 때문에 dp[row - 1][col - 1]을 그대로 가져온다.

즉, dp[row][col] = dp[row - 1][col - 1]

만약, s1[row - 1] != s2[col - 1] 라면, 연산을 따로 수행해줘야 한다.

1. 삽입(insert) : dp[row - 1][col] + 1
2. 삭제(remove) : dp[row][col - 1] + 1
3. 수정(modify) : dp[row - 1][col - 1] + 1

위 3개의 연산 중 가장 작은 값을 dp[row][col]에 넣어준다.

즉, dp[row][col] = min(dp[row - 1][col], dp[row][col - 1], dp[row - 1][col - 1]) + 1 이다.

---

과정 5

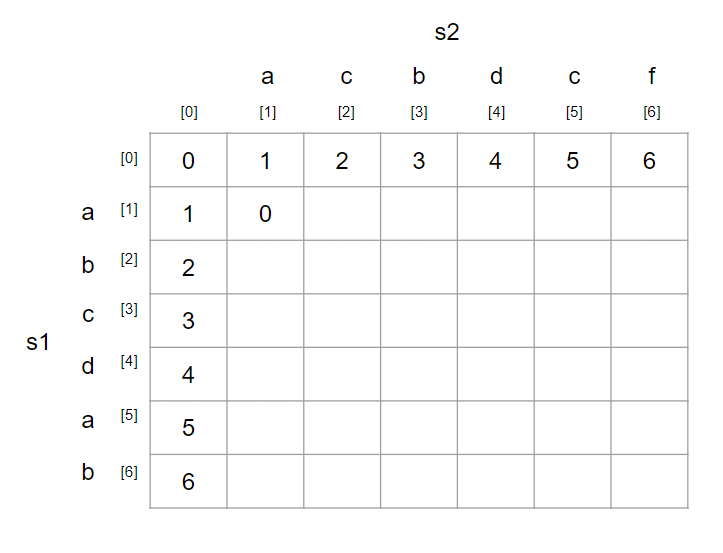
(1, 1)부터 보자. s1[1] = s2[1] 이므로 별도의 연산 없이 (0, 0)의 값을 가져온다.

과정 6

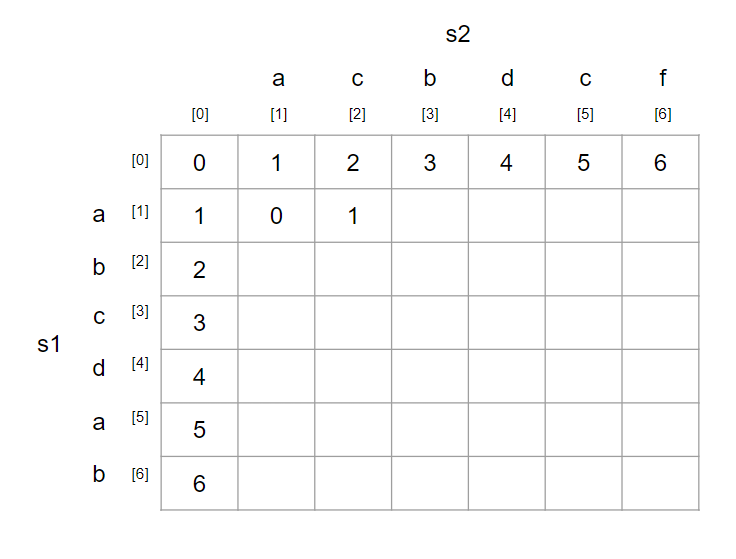
(1, 2)를 보자. s1[1] = a, s2[2] = c 이므로 연산이 필요하다.
위에서 언급한 3가지 연산의 총 연산횟수를 살펴보면,
삽입 : 1 (dp[1][1] + 1)
삭제 : 3 (dp[0][2] + 1)
수정 : 2 (dp[0][1] + 1)
이므로, 제일 최소인 삽입 연산을 수행한다.

과정 7

위의 과정을 반복해서 표를 채우자.

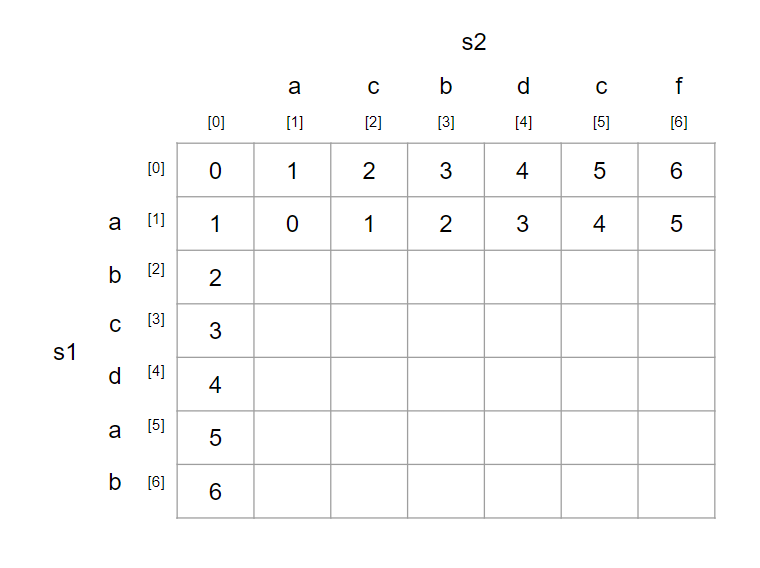
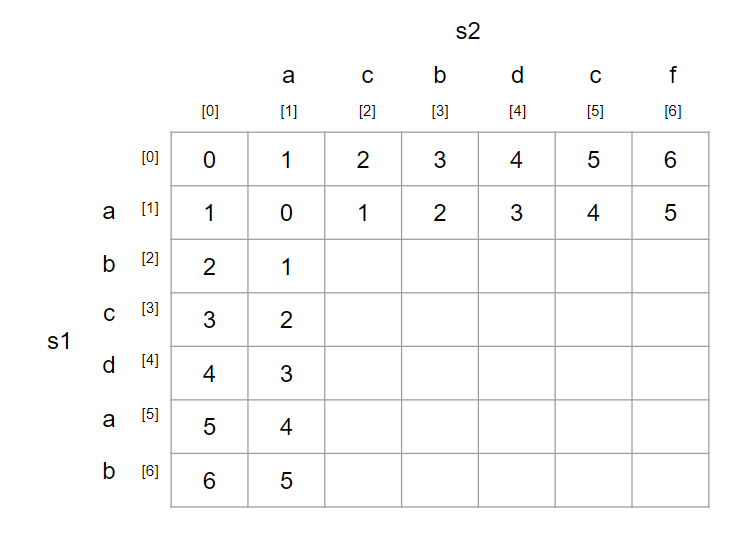
과정 8

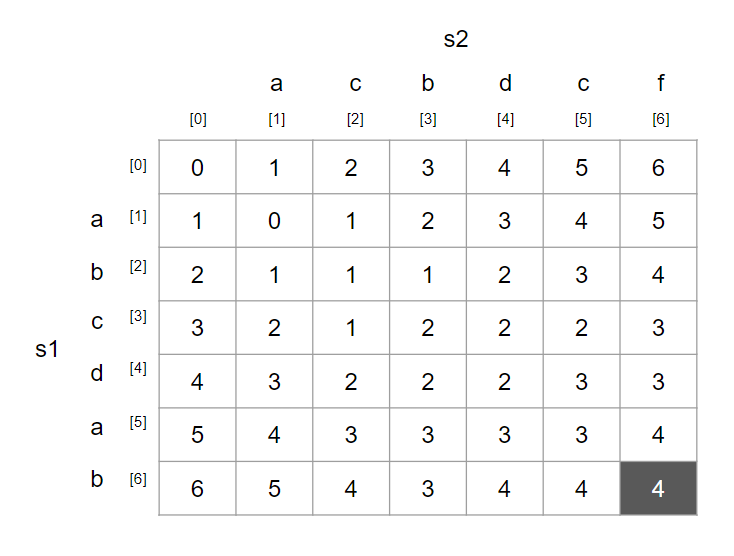
최종적으로는 위의 표가 만들어지고, 우리가 구하고자 하는 값은 맨 오른쪽 아래의 값이다.

코드를 맹글어보자!

def edit_dist(a, b):
    n = len(a)
    m = len(b)
    
    # DP 테이블 초기화
    dp = [[0] * (m + 1) for _ in range(n + 1)]

    # DP 테이블 초기 설정
    for i in range(1, n + 1):
        dp[i][0] = i

    for j in range(1, m + 1):
        dp[0][j] = j

    # 최소 편집 거리 계산
    for i in range(1, n + 1):
        for j in range(1, m + 1):
            
            # 문자가 같다면, 왼쪽 위에 해당하는 수를 그대로 대입
            if a[i - 1] == b[j - 1]:
                dp[i][j] = dp[i - 1][j - 1]
                
            # 문자가 다르다면, 3가지 경우 중에서 최솟값을 대입
            # 삽입(왼쪽), 삭제(위쪽), 교체(왼쪽 위) 중에서 최소 비용을 찾는다.
            else:
                dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
                
    return dp[n][m]

끗-!