
DFS/BFS
| 출제 빈도 | 평균 점수 | 문제 세트 |
|---|---|---|
| 높음 | 낮음 | 5 / 7 |
타겟 넘버
문제 설명
n개의 음이 아닌 정수들이 있습니다. 이 정수들을 순서를 바꾸지 않고 적절히 더하거나 빼서 타겟 넘버를 만들려고 합니다. 예를 들어 [1, 1, 1, 1, 1]로 숫자 3을 만들려면 다음 다섯 방법을 쓸 수 있습니다.
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
사용할 수 있는 숫자가 담긴 배열 numbers, 타겟 넘버 target이 매개변수로 주어질 때 숫자를 적절히 더하고 빼서 타겟 넘버를 만드는 방법의 수를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 주어지는 숫자의 개수는 2개 이상 20개 이하입니다.
- 각 숫자는 1 이상 50 이하인 자연수입니다.
- 타겟 넘버는 1 이상 1000 이하인 자연수입니다.
입출력 예
| numbers | target | return |
|---|---|---|
| [1, 1, 1, 1, 1] | 3 | 5 |
| [4, 1, 2, 1] | 4 | 2 |
입출력 예 설명
입출력 예 #1
문제 예시와 같습니다.
입출력 예 #2
+4+1-2+1 = 4
+4-1+2-1 = 4
- 총 2가지 방법이 있으므로, 2를 return 합니다.
아이디어
- numbers 배열의 앞의 숫자부터 뽑아서, 합에 - or + 를 진행한다.
- 모든 숫자를 사용했고 최종 합이 target과 같으면, 경우의 수 + 1
알고리즘
문제에서 최소 거리 같은 키워드 언급이 없으므로 DFS 사용
코드
answer = 0
def solution(numbers, target):
global answer
n = len(numbers)
def helper(_sum, count, idx): # 총 합, 숫자 사용 개수, 인덱스
global answer
if count == n and _sum == target: # 숫자를 모두 사용했고 총 합이 target과 같을 때
answer += 1 # 경우의 수 + 1
return
if count >= n: # 합이 target과 같지 않다면
return
helper(_sum + numbers[idx], count + 1, idx + 1) # 덧셈
helper(_sum - numbers[idx], count + 1, idx + 1) # 뺄셈
helper(0, 0, 0)
return answer설명
helper: dfs 함수_sum: 숫자를 모두 더한(+,-) 총합count: 사용한 숫자 개수idx: 인덱스(어떤 숫자를 사용할지)n:numbers의 길이
문제에서 숫자들의 순서를 유지한 채 더하거나 빼야한다고 언급되어있다.
따라서, 처음 인덱스는 0으로 시작하고 +, - 이 가능하므로 각 경우의 수를 나누어 재귀호출한다.
이때, count와 idx는 1씩 증가시켜 인자로 넘긴다.
만약, 숫자를 모두 사용했고 총 합이 target과 같다면 경우의 수를 1 증가시킨다.
시간복잡도
다음은 n = 3일 때, 경우의 수를 표현한 그림이다.
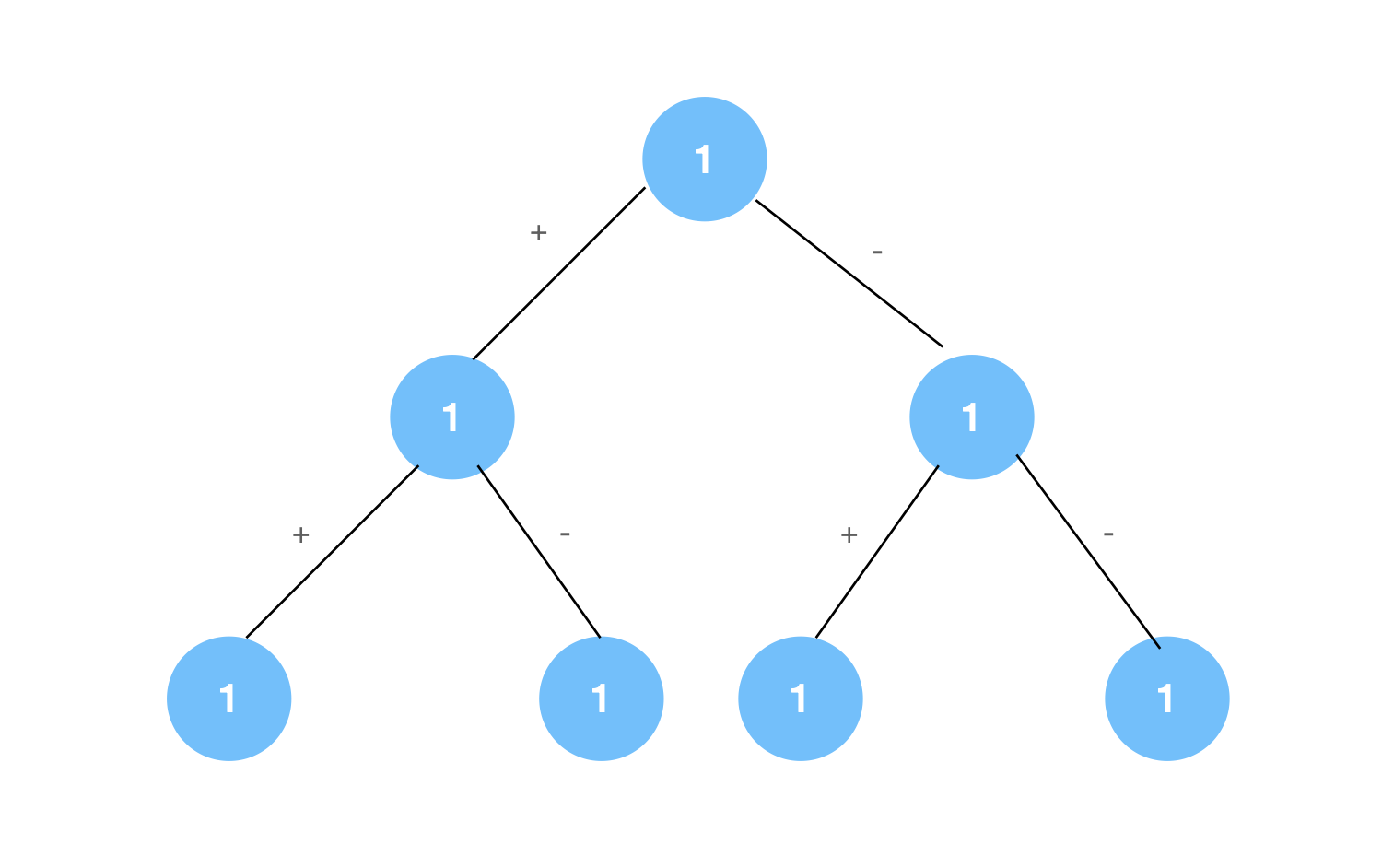
각 number마다 갈래가 2개로 뻗어나가는 트리 형태이다.
그리고 트리의 최대 깊이는 3임을 알 수 있다.
따라서, 최대 깊이는 n이고 갈래가 2개로 뻗어나가므로 임을 알 수 있다.
네트워크
문제 설명
네트워크란 컴퓨터 상호 간에 정보를 교환할 수 있도록 연결된 형태를 의미합니다. 예를 들어, 컴퓨터 A와 컴퓨터 B가 직접적으로 연결되어있고, 컴퓨터 B와 컴퓨터 C가 직접적으로 연결되어 있을 때 컴퓨터 A와 컴퓨터 C도 간접적으로 연결되어 정보를 교환할 수 있습니다. 따라서 컴퓨터 A, B, C는 모두 같은 네트워크 상에 있다고 할 수 있습니다.
컴퓨터의 개수 n, 연결에 대한 정보가 담긴 2차원 배열 computers가 매개변수로 주어질 때, 네트워크의 개수를 return 하도록 solution 함수를 작성하시오.
제한사항
- 컴퓨터의 개수 n은 1 이상 200 이하인 자연수입니다.
- 각 컴퓨터는 0부터
n-1인 정수로 표현합니다. - i번 컴퓨터와 j번 컴퓨터가 연결되어 있으면 computers[i][j]를 1로 표현합니다.
- computer[i][i]는 항상 1입니다.
입출력 예
| n | computers | return |
|---|---|---|
| 3 | [[1, 1, 0], [1, 1, 0], [0, 0, 1]] | 2 |
| 3 | [[1, 1, 0], [1, 1, 1], [0, 1, 1]] | 1 |
입출력 예 설명
예제 #1
아래와 같이 2개의 네트워크가 있습니다.

예제 #2
아래와 같이 1개의 네트워크가 있습니다.

아이디어
- 하나의 컴퓨터를 선택해서 연결된 컴퓨터가 없을 때 까지, 연결된 모든 컴퓨터를 탐색한다. → 함수 재귀호출
- 단, 중복해서 탐색하면 안되므로 방문 배열을 하나 선언해, 방문 표시를 해준다.
- 만약, 연결된 컴퓨터가 없어서 재귀호출이 종료된다면 네트워크의 개수를 1 증가시킨다.
알고리즘
이 문제도 역시 따로 키워드 언급이 없어서 DFS를 사용했다.
코드
연결정보 담는 리스트(graph) 새로 선언
# DFS
def helper(graph, visited, node):
visited[node] = 1 # 방문처리
for nxt in graph[node]: # 연결된 컴퓨터 확인
if not visited[nxt]: # 방문하지 않았다면
helper(graph, visited, nxt) # 다음 컴퓨터를 인자로 재귀호출
def solution(n, computers):
answer = 0
visited = [0] * n # 방문처리 리스트
graph = [[] for _ in range(n)] # 연결되어 있는 컴퓨터들의 정보
# 연결되어 있는 컴퓨터들의 정보만 담는 리스트 초기화
# 인덱스로 정보를 갖는다.
for i in range(n):
for j in range(n):
if i != j:
if computers[i][j] == 1:
graph[i].append(j)
for i in range(n):
if not visited[i]: # 방문하지 않았을 경우에만
helper(graph, visited, i)
answer += 1 # 네트워크 개수 + 1
return answer인자로 주어진 computers(연결정보) 사용
# DFS
def helper(computers, visited, node):
visited[node] = 1 # 방문처리
for i in range(len(computers[node])): # 모든 컴퓨터 확인
if i != node and computers[node][i] == 1 and not visited[i]: # 자기 자신이 아니고 연결되어 있고 방문하지 않았다면
helper(computers, visited, i) # 재귀호출
def solution(n, computers):
answer = 0
visited = [0] * n # 방문처리 리스트
# 컴퓨터 확인
for i in range(n):
if not visited[i]: # 방문하지 않았다면
helper(computers, visited, i)
answer += 1 # 네트워크 개수 + 1
return answer설명
먼저 코드가 2개이다.
- 처음 푼 코드는 인자로 주어진
computers는 인덱스가 아닌 연결인지 아닌지를 나타내기 때문에graph라는 새로운 리스트를 선언해서 각 컴퓨터에 연결된 컴퓨터의 인덱스를 다시 저장했다. - 그리고 한번 탐색한 컴퓨터는 중복해서 탐색하면 안되므로 방문 리스트를 선언했다.
graph에 인덱스를 저장할 때i == j가 같은 경우는 반드시 1이므로 저장하지 않고 넘겼다.- 만약, 현재 컴퓨터를 탐색하지 않았다면
helper(dfs)를 호출한다.- 현재 컴퓨터를 방문처리하고 연결된 컴퓨터를 확인한다.
- 만약, 연결된 컴퓨터가 탐색이 되지 않았다면 해당 컴퓨터를 인자로 넘겨서 재귀 호출을 수행한다.
- 만약, 더 이상 연결된 컴퓨터가 없다면
helper(dfs)가 종료되고 네트워크 수를 1 증가시킨다.(answer += 1)
처음에 graph를 만든 이유는, 인덱스로 편하게 재귀호출을 하기 위해서였다.
생각해보니 따로 연결정보를 저장하는 리스트를 만들면 낭비겠다고 생각했다.
그래서 나머지 로직은 동일하되, 주어진 computers를 그대로 사용했다.
살짝 다른 점은, helper 함수 내부의 for 문이다.
node는 현재 탐색하려는 컴퓨터이고 i는 다음으로 탐색하려는 컴퓨터의 인덱스이다.
이때, 탐색하려는 컴퓨터의 인덱스가 자기 자신이 아닐 때(node == i)만 탐색을 진행하고 현재 컴퓨터와 연결이 되어있어야 한다.(computers[node][i] == 1 )
그리고 연결이 되어있다면, 방문하지 않았어야 한다(not visited[i])
위의 조건 3개가 모두 만족이 되면 인덱스 i를 인자로 재귀호출을 진행한다.
만약, 연결된 컴퓨터가 더 이상 없다면 함수가 종료되고 이때 네트워크의 개수를 1 증가시킨다.
시간복잡도
리스트를 새로 선언한 코드
- 연결된 컴퓨터의 정보만 들어가있다 →
주어진 computers를 사용한 코드
- 모든 노드(컴퓨터)를 탐색한다 →
게임 맵 최단거리
문제 설명
ROR 게임은 두 팀으로 나누어서 진행하며, 상대 팀 진영을 먼저 파괴하면 이기는 게임입니다. 따라서, 각 팀은 상대 팀 진영에 최대한 빨리 도착하는 것이 유리합니다.
지금부터 당신은 한 팀의 팀원이 되어 게임을 진행하려고 합니다. 다음은 5 x 5 크기의 맵에, 당신의 캐릭터가 (행: 1, 열: 1) 위치에 있고, 상대 팀 진영은 (행: 5, 열: 5) 위치에 있는 경우의 예시입니다.

위 그림에서 검은색 부분은 벽으로 막혀있어 갈 수 없는 길이며, 흰색 부분은 갈 수 있는 길입니다. 캐릭터가 움직일 때는 동, 서, 남, 북 방향으로 한 칸씩 이동하며, 게임 맵을 벗어난 길은 갈 수 없습니다.
아래 예시는 캐릭터가 상대 팀 진영으로 가는 두 가지 방법을 나타내고 있습니다.
- 첫 번째 방법은 11개의 칸을 지나서 상대 팀 진영에 도착했습니다.

- 두 번째 방법은 15개의 칸을 지나서 상대팀 진영에 도착했습니다.

위 예시에서는 첫 번째 방법보다 더 빠르게 상대팀 진영에 도착하는 방법은 없으므로, 이 방법이 상대 팀 진영으로 가는 가장 빠른 방법입니다.
만약, 상대 팀이 자신의 팀 진영 주위에 벽을 세워두었다면 상대 팀 진영에 도착하지 못할 수도 있습니다. 예를 들어, 다음과 같은 경우에 당신의 캐릭터는 상대 팀 진영에 도착할 수 없습니다.

게임 맵의 상태 maps가 매개변수로 주어질 때, 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값을 return 하도록 solution 함수를 완성해주세요. 단, 상대 팀 진영에 도착할 수 없을 때는 -1을 return 해주세요.
제한사항
- maps는 n x m 크기의 게임 맵의 상태가 들어있는 2차원 배열로, n과 m은 각각 1 이상 100 이하의 자연수입니다.
- n과 m은 서로 같을 수도, 다를 수도 있지만, n과 m이 모두 1인 경우는 입력으로 주어지지 않습니다.
- maps는 0과 1로만 이루어져 있으며, 0은 벽이 있는 자리, 1은 벽이 없는 자리를 나타냅니다.
- 처음에 캐릭터는 게임 맵의 좌측 상단인 (1, 1) 위치에 있으며, 상대방 진영은 게임 맵의 우측 하단인 (n, m) 위치에 있습니다.
입출력 예
| maps | answer |
|---|---|
| [[1,0,1,1,1],[1,0,1,0,1],[1,0,1,1,1],[1,1,1,0,1],[0,0,0,0,1]] | 11 |
| [[1,0,1,1,1],[1,0,1,0,1],[1,0,1,1,1],[1,1,1,0,0],[0,0,0,0,1]] | -1 |
입출력 예 설명
입출력 예 #1
주어진 데이터는 다음과 같습니다.

캐릭터가 적 팀의 진영까지 이동하는 가장 빠른 길은 다음 그림과 같습니다.

따라서 총 11칸을 캐릭터가 지나갔으므로 11을 return 하면 됩니다.
입출력 예 #2
문제의 예시와 같으며, 상대 팀 진영에 도달할 방법이 없습니다. 따라서 -1을 return 합니다.
아이디어
-
구하고자 하는 것은 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값이다.
-
따라서, BFS를 사용한다.
-
이동한 칸의 개수를 저장하기 위해 덱에 저장하거나 또는 새로운 리스트를 만든다.
-
다음 칸으로 이동할 수 있는지 없는지 판단하기 위해서는,
- 거리 갱신이 이미 이루어졌는지
- 범위에 맞는지
- 벽이 아닌지
→ 위 3개의 조건을 확인해야 한다.
알고리즘
- 지나가야 하는 최소 칸의 개수를 구해야 하므로 BFS를 사용한다.
코드
from collections import deque
dx, dy = [-1, 1, 0, 0], [0, 0, -1, 1] # 상, 하, 좌, 우
INF = int(1e9) # 최대 정수
# 범위 확인
def is_range(x, y, n, m):
return 0 <= x < n and 0 <= y < m
# BFS
def helper(maps, dist, x, y, n, m):
q = deque([(x, y)])
dist[x][y] = 1 # 시작 위치도 칸 개수에 포함
while q:
x, y = q.popleft()
for i in range(4):
nx, ny = x + dx[i], y + dy[i] # 다음 위치 선정
# 범위 포함 & 벽이 아님 & 처음 방문이라면
if is_range(nx, ny, n, m) and maps[nx][ny] != 0 and dist[nx][ny] == INF:
dist[nx][ny] = dist[x][y] + 1 # 거리 갱신
q.append((nx, ny)) # 덱에 추가
def solution(maps):
n, m = len(maps), len(maps[0])
dist = [[INF] * m for _ in range(n)] # 거리 저장 리스트
helper(maps, dist, 0, 0, n, m)
# 이동할 수 없다면 -1, 아니면 최소 칸 개수 출력
return dist[n - 1][m - 1] if dist[n - 1][m - 1] != INF else -1설명
일반적인 BFS 코드와 같다.
시작 위치를 덱에 넣고, 방향을 설정해서 다음 칸을 정한다.
다음 칸이 범위를 벗어나지 않고 이동할 수 있는 칸이고 거리 갱신이 처음이라면(방문이 처음이라면) 다음 칸의 거리 갱신을 해주고 덱에 추가한다.
이를 덱이 비지 않을 때 까지 계속해서 반복한다.
시간복잡도
→ 게임 맵의 크기와 같다.
단어 변환
문제 설명
두 개의 단어 begin, target과 단어의 집합 words가 있습니다. 아래와 같은 규칙을 이용하여 begin에서 target으로 변환하는 가장 짧은 변환 과정을 찾으려고 합니다.
1. 한 번에 한 개의 알파벳만 바꿀 수 있습니다.
2. words에 있는 단어로만 변환할 수 있습니다.
예를 들어 begin이 "hit", target가 "cog", words가 ["hot","dot","dog","lot","log","cog"]라면 "hit" -> "hot" -> "dot" -> "dog" -> "cog"와 같이 4단계를 거쳐 변환할 수 있습니다.
두 개의 단어 begin, target과 단어의 집합 words가 매개변수로 주어질 때, 최소 몇 단계의 과정을 거쳐 begin을 target으로 변환할 수 있는지 return 하도록 solution 함수를 작성해주세요.
제한사항
- 각 단어는 알파벳 소문자로만 이루어져 있습니다.
- 각 단어의 길이는 3 이상 10 이하이며 모든 단어의 길이는 같습니다.
- words에는 3개 이상 50개 이하의 단어가 있으며 중복되는 단어는 없습니다.
- begin과 target은 같지 않습니다.
- 변환할 수 없는 경우에는 0를 return 합니다.
입출력 예
| begin | target | words | return |
|---|---|---|---|
| "hit" | "cog" | ["hot", "dot", "dog", "lot", "log", "cog"] | 4 |
| "hit" | "cog" | ["hot", "dot", "dog", "lot", "log"] | 0 |
입출력 예 설명
예제 #1
문제에 나온 예와 같습니다.
예제 #2
target인 "cog"는 words 안에 없기 때문에 변환할 수 없습니다.
아이디어
- 하나의 알파벳만 바꿀 수 있는데 이를 어떻게 바꿀지가 중요하다.
- 직접 단어를 변경하는 것은 불필요할 수 있다.
- DFS, BFS에서 어떤 조건에서 함수를 종료해야 하는지 기준 설정이 중요하다.
- 인자로 어떤 값들을 넘겨줘야 할지를 잘 판단해야 한다.
알고리즘
- DFS or BFS
코드
BFS - 실패
from collections import deque
# 다른 알파벳이 단 한개인지 확인
def check_digit(begin, target):
diff_count = 0
for x, y in zip(begin, target):
if x != y:
diff_count += 1
return True if diff_count == 1 else False
# BFS
def helper(begin, target, check, words):
q = deque([(begin, 0)])
while q:
cur, count = q.popleft()
# 변환 가능
if cur == target:
return count
for i, word in enumerate(words):
if check_digit(cur, word) and not check[i]:
check[i] = 1
q.append((word, count + 1))
return 0 # 변환할 수 없음
def solution(begin, target, words):
answer = 0
check = [0] * len(words)
if target not in words:
return 0
helper(begin, target, check, words)
return answerDFS - 성공
from collections import deque
answer = int(1e9)
# 다른 알파벳이 단 한개인지 확인
def check_digit(begin, target):
diff_count = 0
for x, y in zip(begin, target):
if x != y:
diff_count += 1
return True if diff_count == 1 else False
# DFS
def dfs(begin, target, count, check, words):
global answer
if begin == target: # 변환 가능
answer = min(answer, count) # 최소 단계 횟수 갱신
return
for i, word in enumerate(words):
if not check[i] and check_digit(begin, word): # 방문 X and 알파벳 한개 차이라면
check[i] = 1 # 방문 처리
dfs(word, target, count + 1, check, words) # 재귀호출
check[i] = 0 # 다음 경우의 수를 위해 방문 처리 해제
def solution(begin, target, words):
check = [int(1e9)] * len(words)
# target이 words에 없다면
if target not in words:
return 0 # 변환 불가능
dfs(begin, target, 0, check, words)
return answerBFS - 성공
from collections import deque
answer = int(1e9)
# 다른 알파벳이 단 한개인지 확인
def check_digit(begin, target):
diff_count = 0
for x, y in zip(begin, target):
if x != y:
diff_count += 1
return True if diff_count == 1 else False
# BFS
def bfs(begin, target, words, check):
global answer
q = deque([(begin, 0)])
while q:
cur, count = q.popleft() # 현재 단어, 단계 횟수
# 변환 가능
if cur == target:
answer = min(answer, count) # 최소 단계 횟수 갱신
continue
for i, word in enumerate(words):
# 알파벳 1개 차이나고 최소 단계 횟수가 더 적을 때
if check_digit(cur, word) and count + 1 < check[i]:
check[i] = count + 1 # 갱신
q.append((word, check[i]))
return 0 # 변환할 수 없음
def solution(begin, target, words):
check = [int(1e9)] * len(words)
# target이 words에 없다면
if target not in words:
return 0 # 변환 불가능
bfs(begin, target, words, check)
return answer설명
먼저, 처음에 BFS로 풀었는데 실패했다. → 원인은 방문 리스트이다.
아래 예시로 어떤 흐름으로 작동하는지 살펴보자.
| begin | target | words |
|---|---|---|
| "hit" | "cog" | ["hot", "dot", "dog", "lot", "log", "cog"] |
먼저, hit은 hot으로 변경이 가능하다.
이후 hot은 dot, lot으로 변경이 가능하다.
dot은 dog로, lot은 log로 변경이 가능하다.
dog는 log, cog로 log는 dog, cog로 변경이 가능하다.
이렇듯, 하나의 단어는 여러 단어로 가지치기가 된다.
처음에는 방문처리를 통해 한번 사용한 단어는 다시는 사용하지 못하게했다.
그러나 위의 예시에서 dog → log, log → dog 경우가 존재할 수 있다.
이때, 우리는 둘 중의 어느 경우의 수가 더 최소인지 판단할 수가 없다.
방문처리 리스트를 활용하게 되면 최소일 수도 있는 경우의 수를 의도치 않게 막아버리게 된다.
그래서 BFS로 풀고자 한다면, 방문처리 리스트가 아닌 누가 최소인지 판단하는 것이 필요하다.
그렇다면 누가 최소인지 어떻게, 무엇으로 판단할 수 있을까?
'가지치기가 되는 단어들을 모두 넣되 최소 단계를 거친 단어만 넣으면 되지 않을까?'
그렇다.
BFS - 성공 코드를 보면 각 단어마다 최소 단계를 저장하는 check 리스트를 사용한다.
이를 사용해서, 단어 A에서 단어 B로 변환이 가능하다면,
단어 B가 가지고 있는 최소 단계 횟수(check[i])와 단어 A가 가지고 있는 단계횟수(count)에 1을 더한 값과 비교한다.
만약 count + 1이 더 작다면 최소 단계를 거쳐서 단어 B로 변환이 가능하다는 의미이므로 check[i]를 count + 1로 갱신하고, 덱에 (단어 B(=word), check[i])를 넣어준다.
DFS는 조합을 구현하는 것과 거의 똑같다.
먼저, 현재 단어 A를 단어 B로 변환할 수 있고 단어 B를 방문하지 않았다면 방문처리를 해주고 재귀호출을 수행한다.
그리고 재귀호출이 끝나면, 다음 경우의 수를 위해 다시 방문 처리를 해제해준다.
종료조건은 begin == target일 때, 최소 단계 횟수를 갱신해주고 종료한다.
시간복잡도
단어의 개수 : N
단어의 길이 : M
- DFS : → 계산을 못하겠다.. 누가 알려주세요
- BFS : → 각 단어마다 모든 단어에 대해 변환 가능한지 확인 + 변환할 때 단어의 길이 만큼 시간 소요
시간복잡도 확실하지 않다. BFS는 인 것 같기도 하고..
여행경로
문제 설명
주어진 항공권을 모두 이용하여 여행경로를 짜려고 합니다. 항상 "ICN" 공항에서 출발합니다.
항공권 정보가 담긴 2차원 배열 tickets가 매개변수로 주어질 때, 방문하는 공항 경로를 배열에 담아 return 하도록 solution 함수를 작성해주세요.
제한사항
- 모든 공항은 알파벳 대문자 3글자로 이루어집니다.
- 주어진 공항 수는 3개 이상 10,000개 이하입니다.
- tickets의 각 행 [a, b]는 a 공항에서 b 공항으로 가는 항공권이 있다는 의미입니다.
- 주어진 항공권은 모두 사용해야 합니다.
- 만일 가능한 경로가 2개 이상일 경우 알파벳 순서가 앞서는 경로를 return 합니다.
- 모든 도시를 방문할 수 없는 경우는 주어지지 않습니다.
입출력 예
| tickets | return |
|---|---|
| [["ICN", "JFK"], ["HND", "IAD"], ["JFK", "HND"]] | ["ICN", "JFK", "HND", "IAD"] |
| [["ICN", "SFO"], ["ICN", "ATL"], ["SFO", "ATL"], ["ATL", "ICN"], ["ATL","SFO"]] | ["ICN", "ATL", "ICN", "SFO", "ATL", "SFO"] |
입출력 예 설명
예제 #1
["ICN", "JFK", "HND", "IAD"] 순으로 방문할 수 있습니다.
예제 #2
["ICN", "SFO", "ATL", "ICN", "ATL", "SFO"] 순으로 방문할 수도 있지만 ["ICN", "ATL", "ICN", "SFO", "ATL", "SFO"] 가 알파벳 순으로 앞섭니다.
아이디어
- 단어 변환처럼 출발지가 같은 경로가 있을 수 있다.
- 즉, 가지치기가 발생할 수 있다는 의미이다.
- 가능한 경로가 2개 이상일 수 있고 가지치기가 존재하므로, 가능한 방법은
- DFS + 방문 처리
- BFS + 우선하는 경로 처리(= 알파벳 순서 처리)
- DFS를 사용한다면, 방문처리를 할 때 주어진
tickets의 인덱스를 방문 처리용 인덱스로 사용했다.(즉,1번 항공권을 방문했다면check[1] = True)
알고리즘
내가 생각한 알고리즘은 일단 아이디어에서 언급했듯이, 가지치기가 발생할 수 있고 가능한 경로가 2가지이므로(사실 가능한 경로가 여러개이다 == 가지치기가 발생한다) 방문처리를 결합한 DFS를 사용했다.
(또는 문제에서 가능한 경로가 여러 개일 경우, 알파벳 순서가 앞서는 경로를 return 하라고 하니, BFS를 사용하면서 덱에 경로를 넣기 전에 알파벳 순서 계산을 하면 된다)
코드
내 코드
from collections import defaultdict
answer = [] # 경로 저장
# DFS
def dfs(n, tickets, check, cnt, prev, way):
if cnt == n: # 모든 경로 탐색함.
answer.append(list(way))
return
# 항공권 탐색
for i, ticket in enumerate(tickets):
# 해당 항공권을 사용하지 않았고, 현재 출발지가 이전 목적지와 같다면
# 즉, 여행경로가 이어진다면
if not check[i] and prev == ticket[0]:
check[i] = True # 방문처리
dfs(n, tickets, check, cnt + 1, ticket[1] , way + [ticket[1]]) # 재귀호출
check[i] = False # 방문처리 해제
def solution(tickets):
n = len(tickets) # 티켓 길이
check = [0] * n # 방문처리 리스트
# 첫 출발지는 무조건 "ICN"
# "ICN"이 여러 개 있을 수 있다.
for i, ticket in enumerate(tickets):
if ticket[0] == "ICN":
check[i] = True # 방문처리
dfs(n, tickets, check, 1, ticket[1], [ticket[0], ticket[1]])
check[i] = False # 방문처리 해제
answer.sort() # 알파벳 순서로 빠른 경로를 위해 정렬
return answer[0] # 첫번째 경로가 가장 빠른 경로임.다른 사람 코드
def solution(tickets):
path = []
# 1. {시작점: [도착점리스트]} 형태로 그래프 생성
graph = defaultdict(list)
for (start, end) in tickets:
graph[start].append(end)
# 2. 도착점 리스트를 역순 정렬
for airport in graph.keys():
graph[airport].sort(reverse=True)
# 3. 출발지는 항상 ICN이므로 stack에 먼저 넣어두기
stack = ["ICN"]
# 4. DFS로 모든 노드 순회
while stack:
# 4-1. 스택에서 가장 위의 저장된 데이터 꺼내오기
top = stack.pop()
# 4-2. top이 그래프에 없거나, top을 시작점으로 하는 티켓이 없는 경우 path에 저장
if top not in graph or not graph[top]:
path.append(top)
# 4-3. top을 다시 스택에 넣고 top의 도착점 중 가장 마지막 지점을 꺼내와 스택에 저장
else:
stack.append(top)
stack.append(graph[top].pop())
# 5. path를 뒤집어서 반환
return path[::-1]모든 testcase가 0.2ms에 끝난다.
접근 방법 참고하려면 여기로
설명
- 문제에서 언급했듯이 처음 출발지는 무조건 "ICN" 이다.
- "ICN"이 출발지인 항공권이 여러 개 있을 수 있으므로
방문처리 → DFS → 방문처리 해제의 과정을 거친다.
- "ICN"이 출발지인 항공권이 여러 개 있을 수 있으므로
- 모든 항공권을 탐색하면서, 현재 항공권의 출발지(
ticket[0])가 이전 목적지(prev)와 같고 현재 항공권을 사용하지 않았다면(not check[i]) 방문처리를 해주고 재귀 호출한다. - 모든 항공권을 탐색했다면, 여행 경로를 저장한다.
- (2)번의 현재 항공권의 방문처리를 해제해준다.
[회고] 경로를 저장하는 거에서 시간을 좀 투자했다.. 그리고 알고리즘은 맞는 것 같은데 계속 []를 반환하길래 살펴보니, 전역변수를 설정해놓고 지역변수에 []를 할당하고 있는 어이없는 실수를 했다..
시간복잡도
어떻게 계산해야 할지..
