
문제 설명
n개의 지점이 있고, 각 지점은 출입구, 쉼터 또는 산봉우리입니다.
지점은 양방향 등산로로 연결되어 있고, 이동하는 데 일정 시간이 소요됩니다.
등산코스는 지점 번호를 순서대로 나열하여 표현하며, 등산 중 쉼터나 산봉우리를 방문할 때마다 휴식을 취할 수 있습니다.
등산코스의 intensity는 휴식 없이 이동하는 가장 긴 시간입니다.
당신은 출입구에서 시작하여 한 곳의 산봉우리만 방문한 후 다시 출입구로 돌아오는 등산코스를 최소 intensity로 정하려고 합니다.
등산코스에서 출입구는 처음과 끝에 한 번씩, 산봉우리는 한 번만 포함되어야 합니다.
즉, 출입구 → 쉼터 → 산봉우리 → 쉼터 → 출입구(처음 출입구와 같은) 이다.
intensity가 최소가 되는 등산코스에 포함된 산봉우리 번호와 intensity의 최솟값을
[산봉우리 번호, intensity 최솟값] 형태로 return 하세요.
단, intensity가 최소가 되는 등산코스가 여러 개라면 그중 산봉우리의 번호가 가장 낮은 등산코스를 선택한다.
- 위 그림에서 원에 적힌 숫자는 지점의 번호를 나타내며, 1, 3번 지점에 출입구, 5번 지점에 산봉우리가 있습니다. 각 선분은 등산로를 나타내며, 각 선분에 적힌 수는 이동 시간을 나타냅니다. 예를 들어 1번 지점에서 2번 지점으로 이동할 때는 3시간이 소요됩니다.
등산코스를 1-2-4-5-6-4-2-1 과 같이 정했을 때의 이동경로를 그림으로 나타내면 아래와 같습니다.
이때, 휴식 없이 이동해야 하는 시간 중 가장 긴 시간은 3시간입니다. 따라서 이 등산코스의 intensity는 3이며, 이 보다 intensity가 낮은 등산코스는 없습니다.

가능한 intensity의 최솟값은 4이며, intensity가 4가 되는 등산코스는 1-4-1과 1-7-3-7-1 이 있습니다. intensity가 최소가 되는 등산코스가 여러 개이므로 둘 중 산봉우리의 번호가 낮은 1-7-3-7-1 을 선택합니다. 따라서 [3, 4]를 return 해야 합니다.
제한 사항
- 2 ≤
n≤ 50,000 n- 1 ≤paths의 길이 ≤ 200,000paths의 원소는[i, j, w]형태입니다.i번 지점과j번 지점을 연결하는 등산로가 있다는 뜻입니다.w는 두 지점 사이를 이동하는 데 걸리는 시간입니다.- 1 ≤
i<j≤n - 1 ≤
w≤ 10,000,000 - 서로 다른 두 지점을 직접 연결하는 등산로는 최대 1개입니다.
- 1 ≤
gates의 길이 ≤n- 1 ≤
gates의 원소 ≤n gates의 원소는 해당 지점이 출입구임을 나타냅니다.
- 1 ≤
- 1 ≤
summits의 길이 ≤n- 1 ≤
summits의 원소 ≤n summits의 원소는 해당 지점이 산봉우리임을 나타냅니다.
- 1 ≤
- 출입구이면서 동시에 산봉우리인 지점은 없습니다.
gates와summits에 등장하지 않은 지점은 모두 쉼터입니다.- 임의의 두 지점 사이에 이동 가능한 경로가 항상 존재합니다.
- return 하는 배열은
[산봉우리의 번호, intensity의 최솟값]순서여야 합니다.
아이디어
- 문제는 출입구에서 시작하여 특정 산봉우리로 가는 최소
intensity를 구하는 것이다.- 이는 다익스트라 알고리즘과 유사하다.
- → 특정 노드에서 출발해 다른 특정 노드로 가는 최단 경로 알고리즘
- 단, 경로를 확인할 때 기준을 가중치의 합이 아닌
intensity를 설정했다.
- 이는 다익스트라 알고리즘과 유사하다.
- 등산코스는
출입구 → 쉼터 → 산봉우리 → 쉼터 → 출입구(처음 출입구와 같은)를 만족한다.- 이때, 산봉우리까지 갔다가 다시 되돌아오는 경우는 처음과 같은 경로를 선택하면 되므로 고려하지 않아도 된다.
- 즉, 편도 경로(
출입구 → 쉼터 → 산봉우리)만 구하면 된다.
- 최소가 되는 등산코스가 여러 개라면 그 중 산봉우리 번호가 가장 낮은 등산코스를 선택해야 한다.
- 처음에 산봉우리(
summits) 오름차순 정렬을 수행하면 해결할 수 있다.
- 처음에 산봉우리(
n의 최대 크기가 50,000이기 때문에, 다익스트라를 처음 수행할 때 모든 출입구를 heap에 넣고 시작해야 한다.- 만약, 출입구마다 다익스트라를 수행한다면 시간초과가 발생할 수 있다.
코드
실패코드
import heapq
INF = int(1e9)
def solution(n, paths, gates, summits):
# 다익스트라
def dijkstra():
q = []
dist = [INF] * (n + 1) # 거리 정보 초기화
# 모든 출입구 넣기
for gate in gates:
dist[gate] = 0
heapq.heappush(q, (0, gate))
while q:
intensity, cur = heapq.heappop(q) # intensity가 가장 작은 것을 먼저 꺼낸다.(즉, 출입구부터 꺼내게 됨)
# 최소 intensity를 구해야 하므로
# 산봉우리거나 더 큰 intensity라면 이동하지 않는다.
if cur in summits or dist[cur] < intensity:
continue
# 이동해본다.
for w, nxt in edges[cur]:
cost = max(w, intensity) # 휴식없는 가장 긴 시간이므로
if cost < dist[nxt]:
dist[nxt] = cost
heapq.heappush(q, (cost, nxt))
# 최소 intensity 찾기
ret = [summits[0], dist[summits[0]]]
for summit in summits:
if dist[summit] < ret[1]:
ret[0] = summit
ret[1] = dist[summit]
return ret
# intensity가 최소가 되는 산봉우리가 여러 개일 때
# 산봉우리의 번호가 가장 낮은 등산코스를 선택하기 위해 정렬
summits.sort()
edges = [[] for _ in range(n + 1)]
# 양방향 등산로 정보 초기화
for path in paths:
i, j, w = path
edges[i].append((w, j))
edges[j].append((w, i))
# 다익스트라 수행
answer = dijkstra()
return answer설명
일단 계속해서 테스트케이스 25번이 시간초과가 났다.
테스트 13 〉 통과 (8.55ms, 11.6MB)
테스트 14 〉 통과 (40.90ms, 20MB)
테스트 15 〉 통과 (303.95ms, 74.3MB)
테스트 16 〉 통과 (375.93ms, 77.1MB)
테스트 17 〉 통과 (385.67ms, 77MB)
테스트 18 〉 통과 (17.86ms, 15.4MB)
테스트 19 〉 통과 (141.27ms, 34MB)
테스트 20 〉 통과 (326.29ms, 71MB)
테스트 21 〉 통과 (412.63ms, 68MB)
테스트 22 〉 통과 (200.47ms, 14.8MB)
테스트 23 〉 통과 (2296.10ms, 30.9MB)
테스트 24 〉 통과 (2288.53ms, 26.6MB)
테스트 25 〉 실패 (시간 초과)summits의 최대 크기가 n이고, n의 최대 크기는 50,000이다.
q를 순회할 때 cur in summits에서 in은 이 소요된다. (리스트는 , 집합은 )
성공코드
import heapq
INF = int(1e9)
def solution(n, paths, gates, summits):
# 다익스트라
def dijkstra():
q = []
dist = [INF] * (n + 1) # 거리 정보 초기화
# 모든 출입구 넣기
for gate in gates:
dist[gate] = 0
heapq.heappush(q, (0, gate))
while q:
intensity, cur = heapq.heappop(q)
# 최소 intensity를 구해야 하므로
# 산봉우리거나 더 큰 intensity라면 이동하지 않는다.
if cur in summits_set or dist[cur] < intensity:
continue
# 이동해본다.
for w, nxt in edges[cur]:
new_intensity = max(w, intensity) # 휴식없는 가장 긴 시간이므로
# new_intensity는 확인할 경로의 intensity이고
# dist[nxt]는 이미 저장된 nxt까지의 경로의 intensity이다.
# nxt 위치에 더 작은 intensity로 도착한 적이 있다면
# 큐에 넣지 않는다.
if new_intensity < dist[nxt]:
dist[nxt] = new_intensity
heapq.heappush(q, (new_intensity, nxt))
# 최소 intensity 찾기
ret = [summits[0], dist[summits[0]]]
for summit in summits:
if dist[summit] < ret[1]:
ret[0] = summit
ret[1] = dist[summit]
return ret
# intensity가 최소가 되는 산봉우리가 여러 개일 때
# 산봉우리의 번호가 가장 낮은 등산코스를 선택하기 위해 정렬
summits.sort()
summits_set = set(summits)
edges = [[] for _ in range(n + 1)]
# 양방향 등산로 정보 초기화
for path in paths:
i, j, w = path
edges[i].append((w, j))
edges[j].append((w, i))
answer = dijkstra()
return answer설명
new_intensity: 새로운 intensitynxt: 다음노드w: nxt가 가지는 intensity(=nxt로 들어가는 intensity)cur: 현재노드
아이디어에서 언급했듯이, 개선된 다익스트라 알고리즘을 활용한다.
(단, 기준은 가중치의 합이 아닌 intensity이다.)
먼저, heap에 모든 출입구를 intensity는 0으로 설정하고 (0, 출입구) 형태로 넣어준다.
해당 heap을 순회하면서,
- 만약, 현재 노드가 산봉우리라면, 큐에 넣지 않는다(
continue) → 산봉우리까지의 편도 경로만 구하면 되므로.. - 만약, 현재 노드까지의 경로가 이미 처리되었고
intensity보다 작다면 큐에 넣지 않는다. → 문제에서최소 intensity를 구해야 하므로
자 이제 연결된 노드로 이동을 해보자.
이때 새로운 intensity의 설정을 어떻게 하느냐가 중요하다.
intensity[to 현재노드의 intensity]와 w[from 현재노드 to 다음노드의 intensity]를 비교해서 큰 값을 새로운 intensity로 설정한다.
그림으로 보면 다음과 같다.
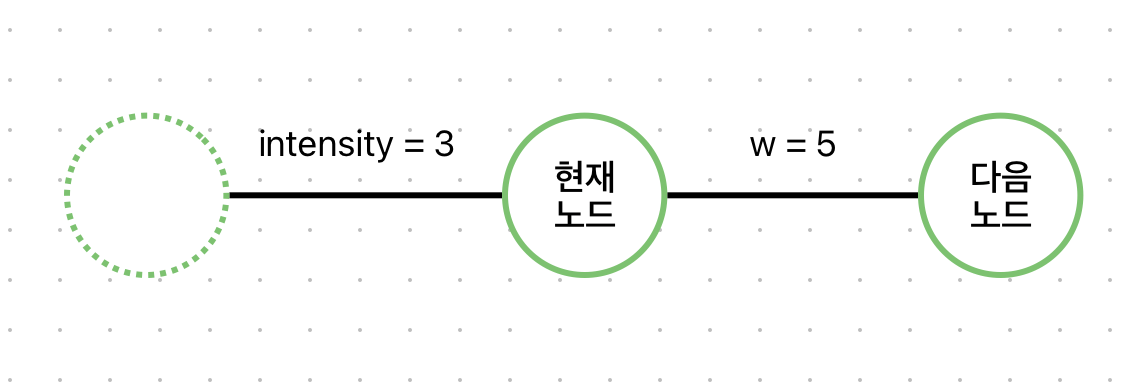
그리고나서 다음노드까지의 경로의 intensity(dist[nxt])와 새로운 intensity를 비교한다.
dist[nxt]가 의미하는 것은 어떤 특정 노드에서 시작해서 nxt까지의 경로의 intensity를 의미한다.
즉, 이미 구한 경로의 intensity이다.
우리가 구하고자 하는 것은 여러 경로 중 최소 intensity를 갖는 경로이므로, 새로운 intensity가 더 작다면 갱신하고 heap에 (새로운 intensity, 다음노드)를 넣어준다.
(여기서 dist[다음노드] 는 7 → 5로 갱신됨.)
이를 그림으로 살펴보면 다음과 같다.
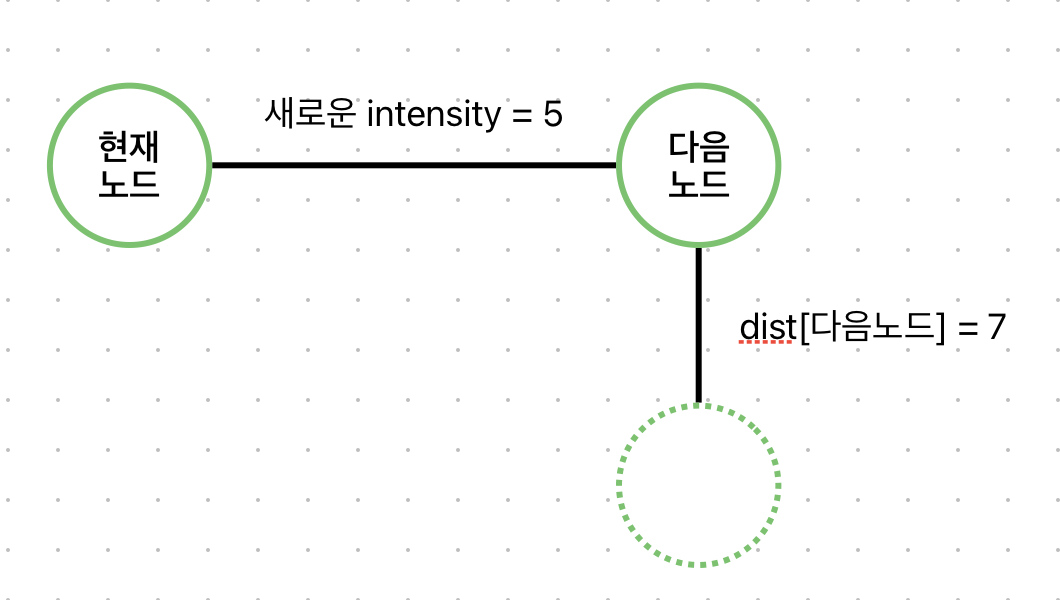
시간복잡도
단순하게 살펴봤을 때,
- 간선의 개수 : E
- 노드의 개수 : V
→



