모폴로지 연산은 물체의 모양을 분석하거나 원하는 형태로 바꾸는 작업에
유용하게 사용될 수 있다고 한다.
특정 부분을 강조하거나 잡음을 제거하는 등에 사용할 수 있다.
이진 모폴로지
모폴로지의 기본적인 두 가지 연산은 팽창과 침식이 있다.
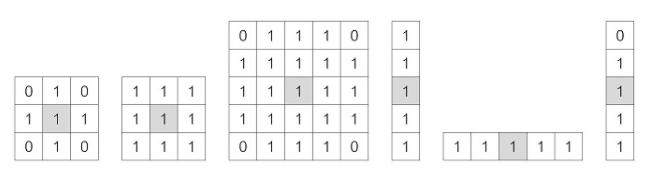
팽창은 영상의 255인 화소에 구조요소를 씌워 구조요소가 1인 부분과
겹치는 부분은 모두 255로 바꾼다.(합집합)
침식은 영상에 구조요소를 씌웠을 때 겹치는 곳이 모두 255인 경우에만
255로 바꾼다.(교집합)
대표적인 구조요소는 아래와 같다.
팽창과 침식 연산을 이용해 열기와 닫기 연산을 할 수 있다.
열기 연산은 침식 이후 팽창
닫기는 팽창 이후 침식이다.
명암 모폴로지
이진 영상에서는 움푹 패인 곳을 메우거나 튀어나온 곳을 깎는 역할이 주였다면, 명암에서는 명암값을 높이로 보고 골짜기를 메우거나 봉우리를 깎는 상태로 생각해야 한다.
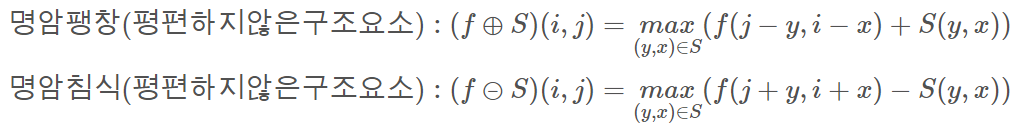

이진 모폴로지에서는 0인 부분은 사실 의미가 없었지만 명암 모폴로지에서는 최대, 최소를 뽑을 때 관여를 하기 때문에 0을 무시할 수 없다. 그래서 연결요소가 모두 0으로 이루어진 평편하지 않은 구조요소에는 아래와 같은 식을 적용할 수 있다.
명암모폴로지에서도 이진모폴로지와 같이 열기와 닫기 연산을 정의할 수 있다.
연결요소를 어떻게 구성하고 어떤 순서로 적용하는 가에 따라 다른 효과가 생기므로 문제에 따라 여러가지 적용을 해보고 경험을 쌓는 것이 중요하다고 한다.
모폴로지의 코드는 각 영상의 연결요소 사이즈만큼 연결요소가 1인 부분만 보거나, 명암에서는 더해서 최대, 최소값을 취해줘 이미 앞에 포스팅 내용들을 봤다면 충분히 구현할 수 있기에 넘어간다.
이미지 참조 : https://songminkee.github.io/studyblog/computer%20vision/2020/05/30/morphology.html
내용 참조 : 컴퓨터비전(저자 오일석)
