컴퓨터비전
1.영상의 이진화

영상의 이진화란 모든 픽셀을 두가지 즉 흑과 백으로만 표현하는 영상을 말한다.왼쪽도 흑과 백으로 착각할 수 있지만 저것은 밝기값이 0 ~ 255까지 가지는 이미지이다.그럼 이진화를 어떻게 할 수 있을까?단순하게 접근을 하면 픽셀값이 일정값을 넘으면 백, 일정값보다 낮으
2.Opencv pixel접근
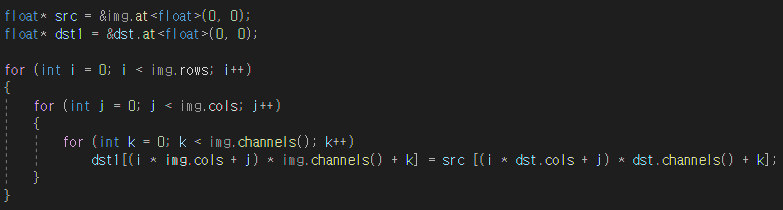
OpenCV에는 Mat이라는 자료형이 있다.보통 imread라는 함수로 이미지를 읽는데컬러이미지 같은 경우 unsigned char의 자료형으로 이미지의 width height 3의 크기로흑백이미지는 unsigned char의 자료형으로 width height의
3.히스토그램 평활화
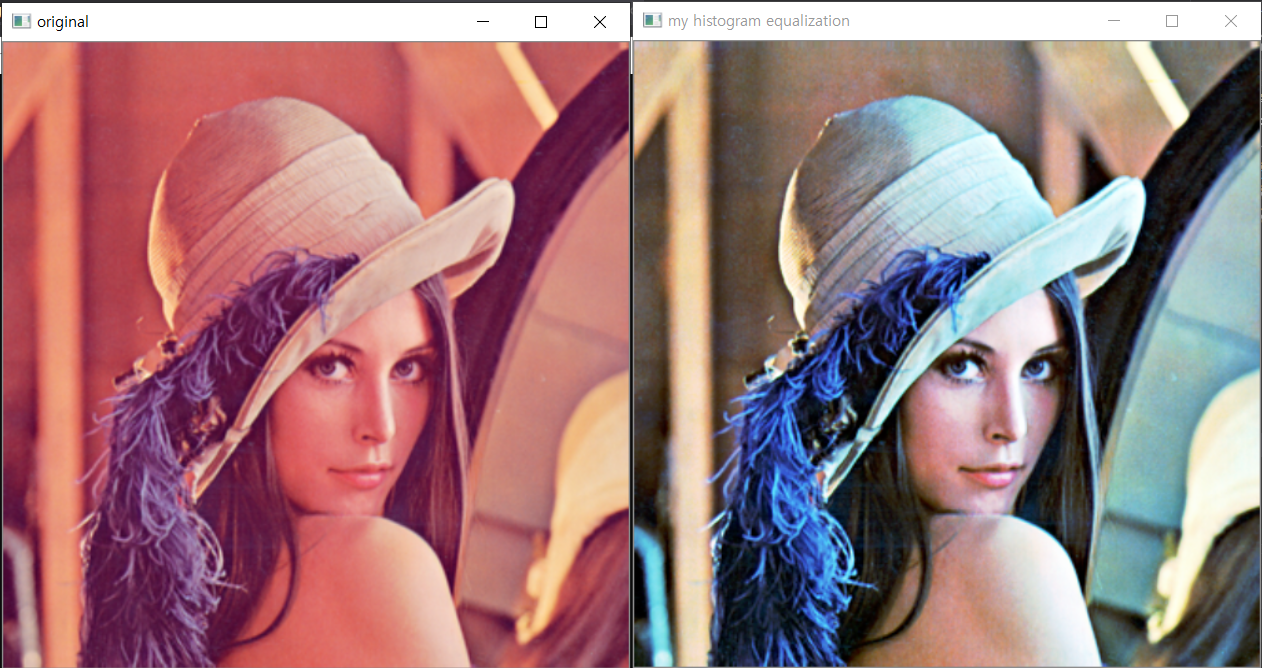
히스토그램(histogram)은 표로 되어 있는 도수 분포를 정보 그림으로 나타낸 것이다. 더 간단하게 말하면, 도수분포표를 그래프로 나타낸 것이다. 보통 히스토그램에서는 가로축이 계급, 세로축이 도수를 뜻하는데, 때때로 반대로 그리기도 한다.= 위키백과 =이미지에서
4.Affine 변환
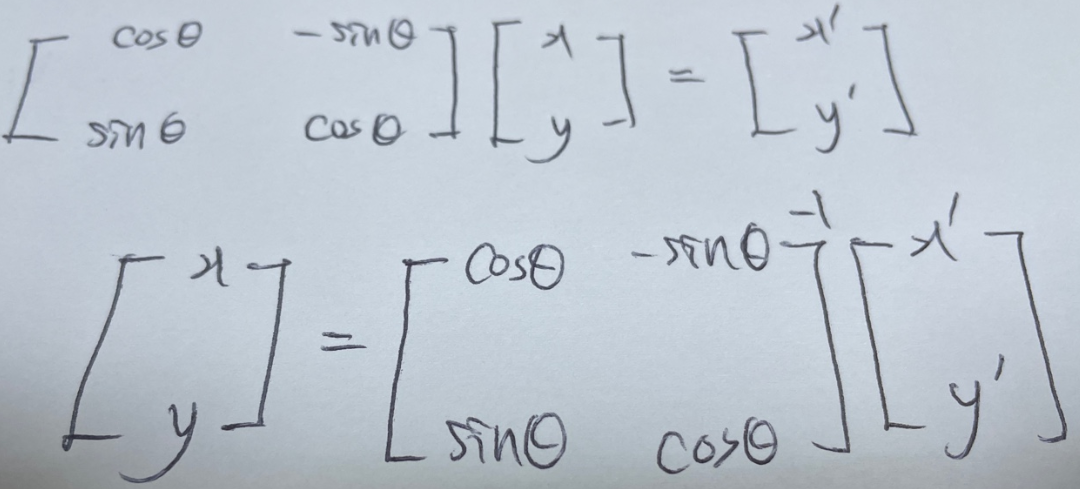
이미지 변환에는 여러가지가 있다대표적으로는 확대, 축소, 회전 등이 있다. 이런 변환들 중에서 점, 직선, 평면을 보존하는 선형 매핑을 Affine변환이라고 한다. 즉, 아핀 변환 후에도 평행한 선들이 그대로 평행하게 유지된다.여기서는 shear, scaling, ro
5.Perspective 변환
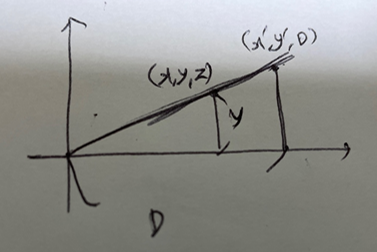
지난 글에서 affine transformation을 다뤘다. 회전, 이동, shear 변환들로 총 자유도가 6인 행렬을 곱해 구할 수 있었다.하지만, affine 변환은 평행한 선들이 유지된 채로 변환이 되는 것이었는데 평행이 유지되지 않은 채 변환되는 것은 어떻게
6.선형보간법
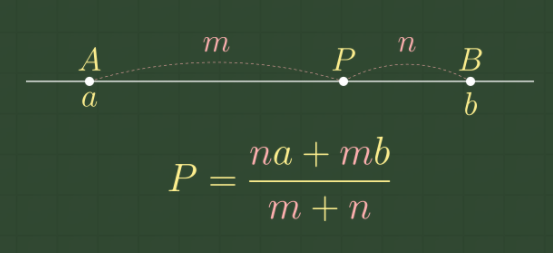
보간법에는 선형보간법만 있지는 않지만 이번에 살펴볼 것은 선형보간법이다.선분의 내분점이 원리가 된다.이 공식만 알고 있다면 이해하는데 전혀 지장이 없다. 이 1차원에서 진행되었던 것을 이미지 즉 2차원으로 확장하는 것이다.픽셀간의 차이가 1이기 때문에 1 - alpha
7.이미지 레이블링
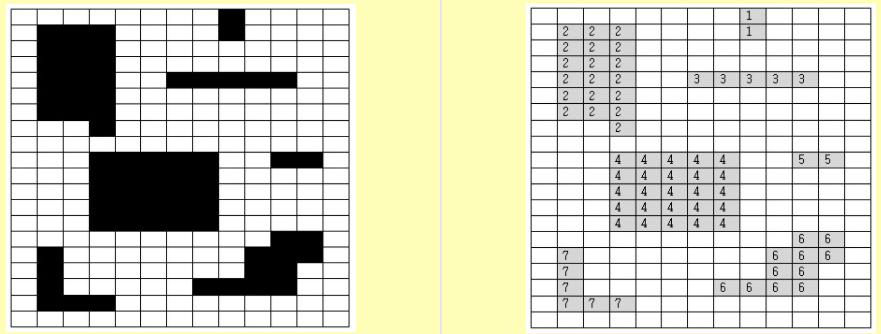
이진 영상을 살펴보면 서로 연결된 화소의 집합이 여럿 나타난다. 이들 집합 각각을 연결요소라 부른다.보통 연결요소는 별도로 다루기 때문에, 이들 각각에 고유한 번호를 붙인 후 다음 처리 단계로 넘겨줘야 한다.이 연결된 요소를 판단하기 위해 4-연결성과 8연결성이 있다.
8.디졸브 효과

많이 볼 수 있는 효과인데, 한 이미지에서 다른 장면으로 넘어갈 때 서서히 넘어가는 효과를 디졸브 효과라고 한다.구현은 매우 간단하다.기존 이미지 : f1바뀔 이미지 : f2출력 이미지 : f3$f3 = \\alpha f1 + (1 - \\alpha)f2$alpha는
9.컨볼루션과 상관
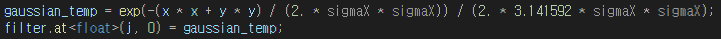
지금까지 봐왔던 영상처리 기술들은 모두 한 점을 보고 다른 점을 계산해는 형태로 진행되었습니다. 이번에 살펴볼 것은 영역 연산이다.해당 점만 보는 것이 아닌 이웃 픽셀들을 참고하여 계산하는 연산이다.이렇게 하면 이미지의 공간적인 정보를 유지할 수 있다.상관은 위의 이미
10.다해상도
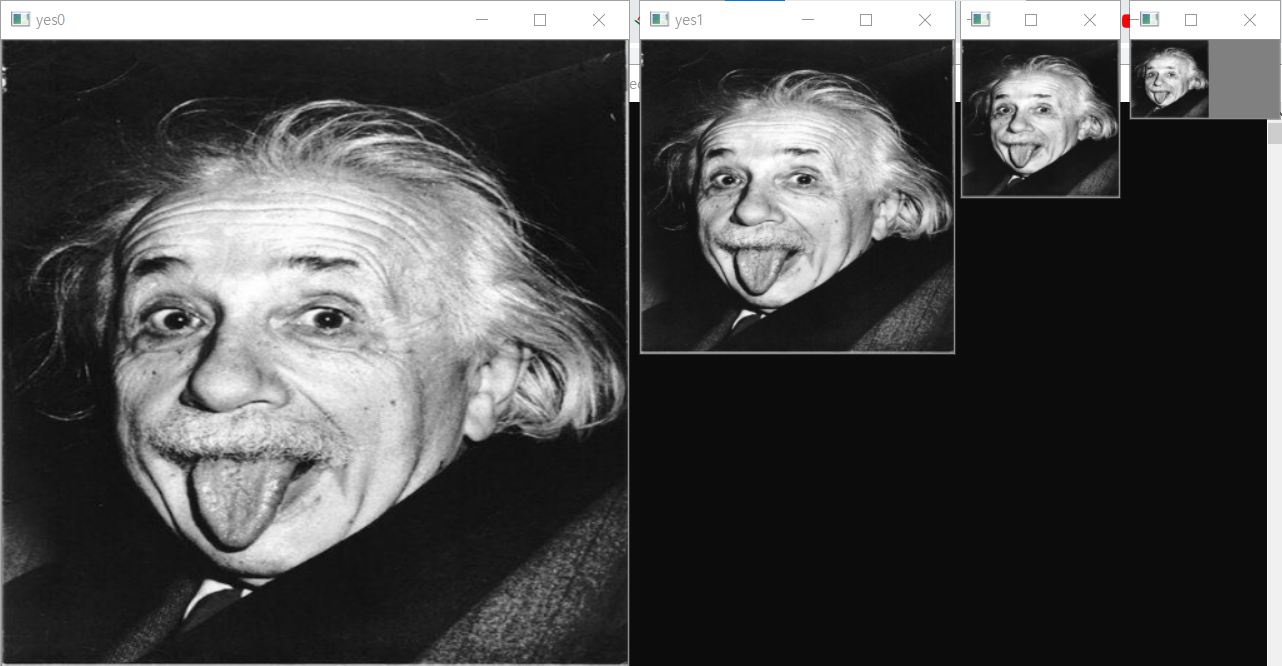
업샘플링 : 해상도를 늘리는 영상처리 연산 다운샘플링 : 해상도를 줄이는 연산 어떤 영상에서는 물체가 영상 전체를 덮을 정도로 크게 나타날 수 있고 다른 영상에서는 아주 작게 나타날 수 있다. 이처럼 다양한 상황에 상관없이 물체를 안정적으로 찾기 위해 고안된 기법이
11.모폴로지 연산
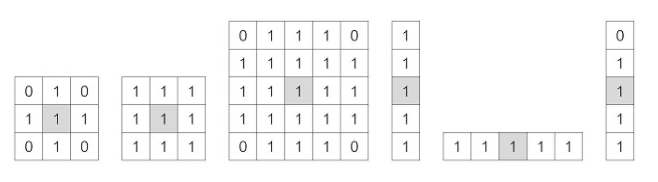
모폴로지 연산은 물체의 모양을 분석하거나 원하는 형태로 바꾸는 작업에 유용하게 사용될 수 있다고 한다.특정 부분을 강조하거나 잡음을 제거하는 등에 사용할 수 있다.모폴로지의 기본적인 두 가지 연산은 팽창과 침식이 있다.팽창은 영상의 255인 화소에 구조요소를 씌워 구조
12.컬러모델
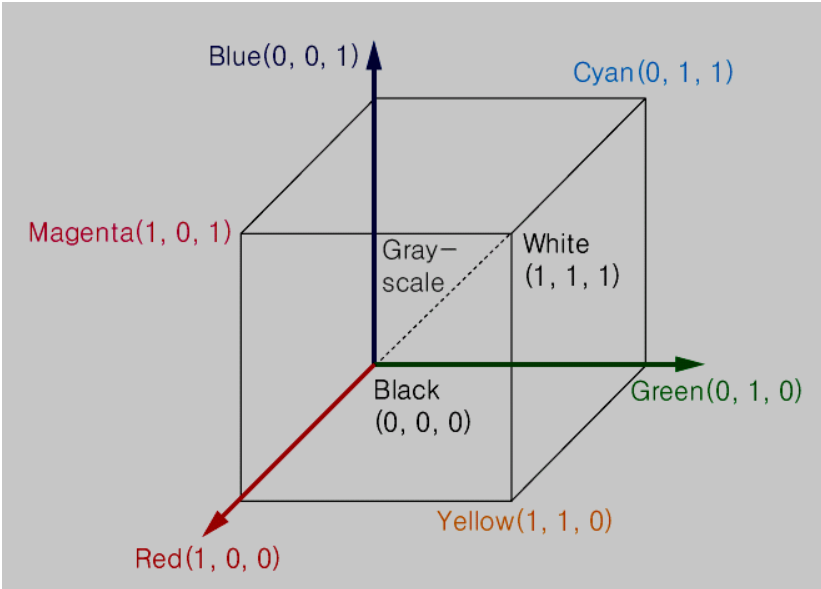
이미 구현할 때에는 컬러 영상에도 적용을 했지만 컬러 영상이 흑백 영상과 어떻게 다르게 되어있는 지는 언급한 적이 없다.컬러영상을 어떻게 나타내는 지 한 번 알아보자가장 널리 사용되는 모델은 RGB모델이다.컴퓨터에서는 이를 나타내기 위해 양자화한다. 길이가 1인 구간을
13.에지 검출의 기초
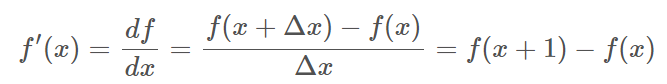
영상에서 에지만 있어도 원래 영상을 거의 그대로 해석할 수 있다.게다가 에지 영상은 이진 영상이므로 원래 영상에 비해 필요한 메모리가 적다그러므로 에지는 매우 유용하다. 그럼 에지를 어떻게 검출할까물체의 경계에서는 명암값에 급격한 변화가 일어난다.즉, 에지는 영상의 명
14.영교차이론

이전 포스팅에서 가우시안 마스크를 아주 가볍게 소개한 적이 있다. 에지 연산에서 미분연산을 적용하기 전에 가우시안을 스무딩하는 전처리 과정을 중요하게 생각했는데 가우시안 스무딩은 두 가지 효과를 제공한다. 잡음 대처 (미분은 잡음을 증폭하므로 스무딩은 중요하다) $
15.캐니 에지
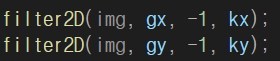
현재 가장 널리 사용되는 에지 검출 연산자이다. 기존의 휴리스틱한 방식을 뛰어넘어, 에지 검출을 최적화 문제로 취급했다. 에지 알고리즘이 갖추어야 할 세 가지 기준을 아래와 같이 제시했다. 최소 오류율 : 거짓 긍정과 거짓 부정이 최소여야 한다. 없는 에지가 생성되거