N-Queen

문제

N-Queen문제는 크기가 NXN인 체스판위에 퀸 N개를 서로 공격할 수 없게 퀸을 놓는 방법의 수를 구하는 문제입니다.

제약조건
1 <= N <= 15

풀이

체스판을 3가지 관점에서 바라봅니다.

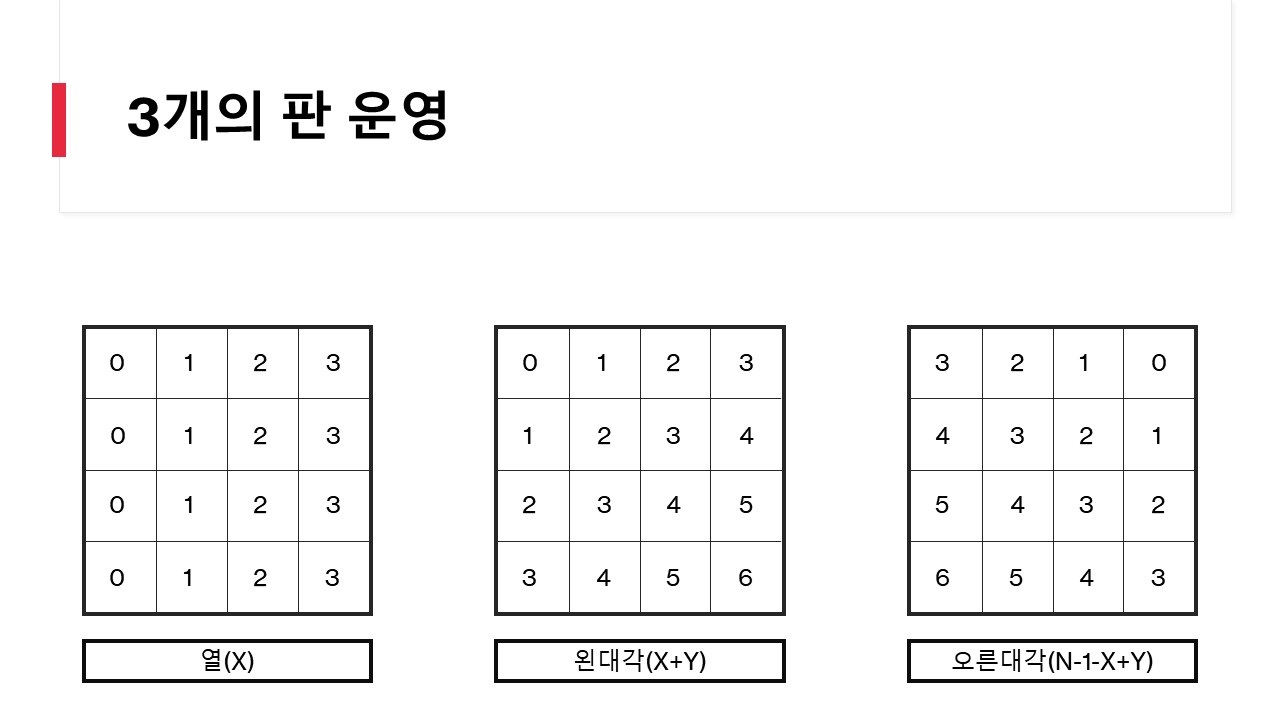
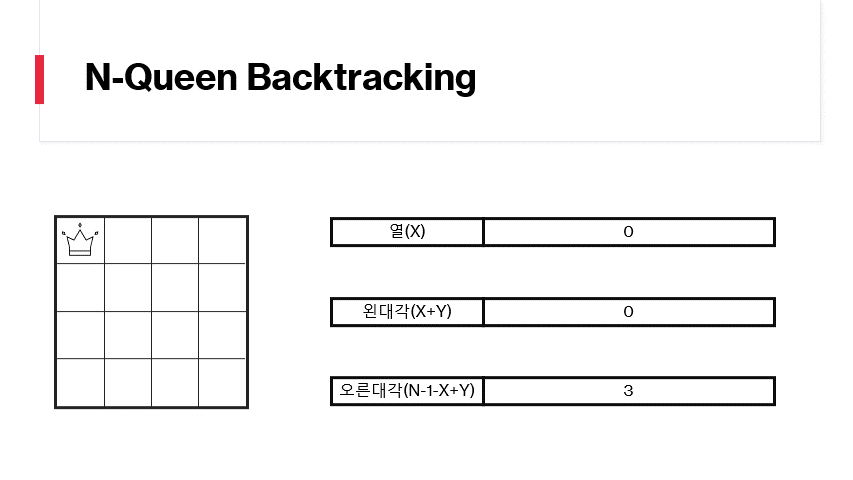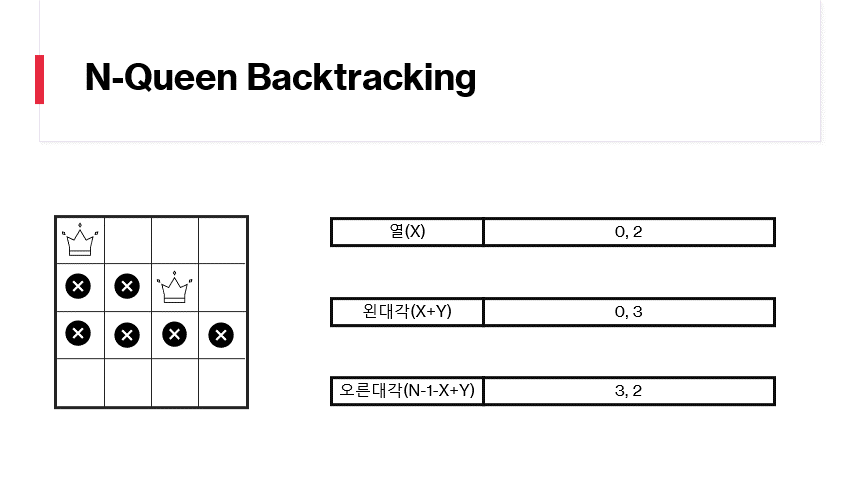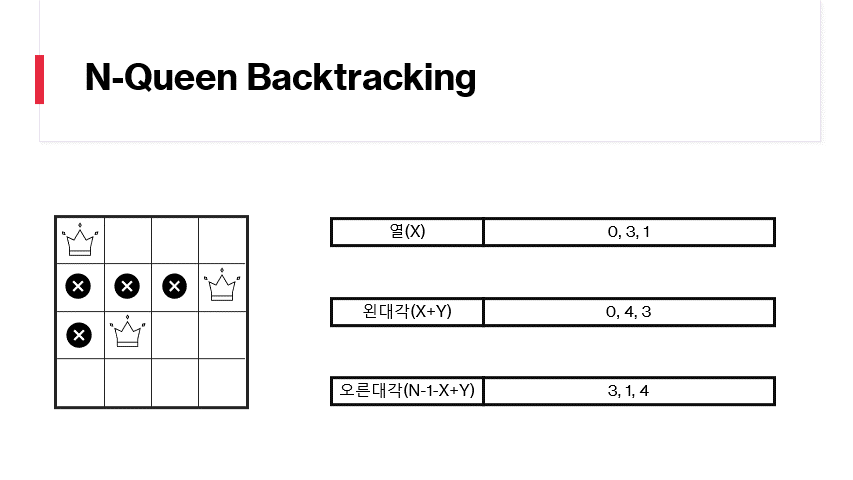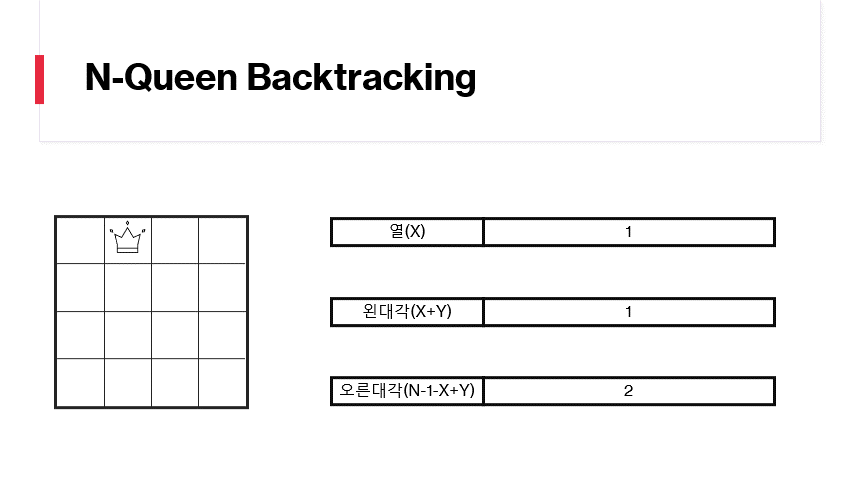
특정 좌표에 퀸을 위치시킬때 퀸의 위치에 해당하는 번호를 추가합니다. 예를 들어 0,0에 퀸을 위치시킨다면 열에는 0, 왼대각에는 0, 오른대각에는 3을 추가합니다. 이후 연산에서 중복된 값이 3개의 판중 하나에도 존재한다면 해당 위치는 놓을수 없는 위치입니다. 행 단위로 검사를 실행하므로 행을 위한 판은 운영하지 않습니다.

행을 끝까지 검사했다면 이전행으로 돌아갑니다(backtracking)
행 검사시에 열/왼대각/오른대각에 없는 번호를 가진 위치는 추가하고 재귀호출을 통하여 다음 행을 검사하게 합니다. 행은 0번째부터 N-1번째 까지 존재합니다. N번째 행을 검사한다는것은 0번째부터 N-1번째까지 퀸이 채워졌다는 의미이고, 더이상 재귀호출을 할수없기 때문에 정답처리를 합니다.

성공하는 경우는 다음과 같습니다.

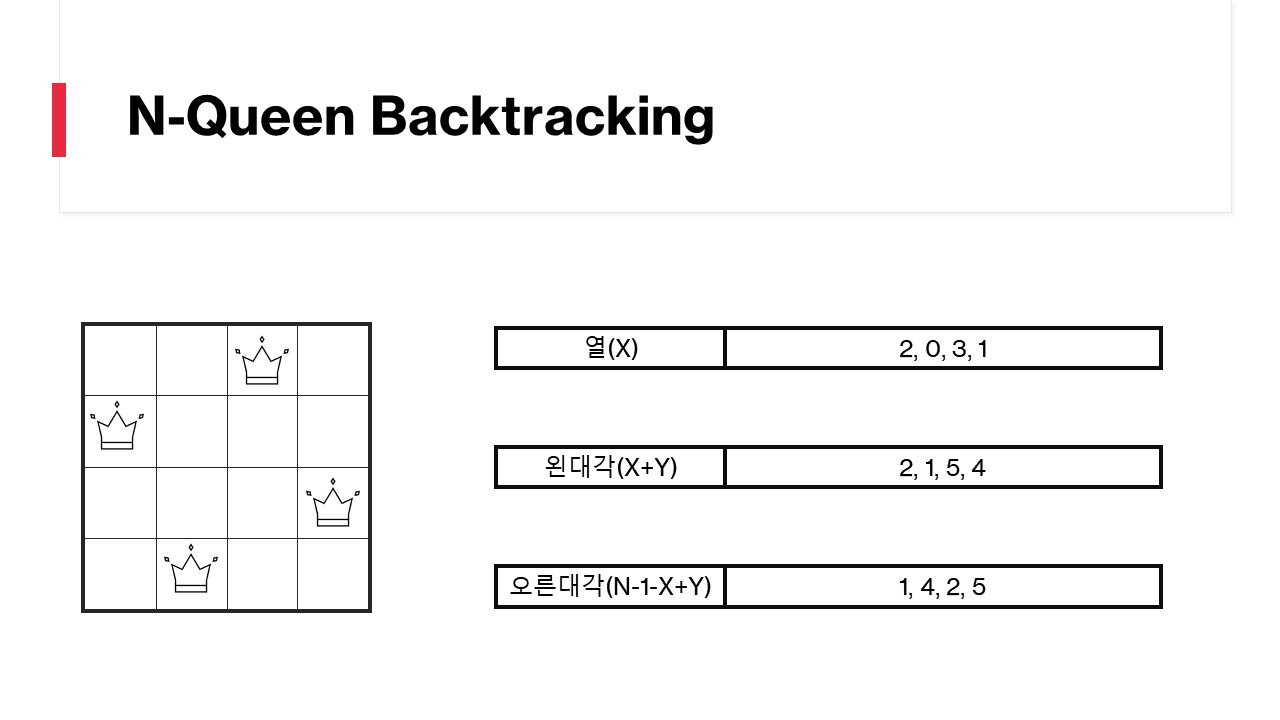
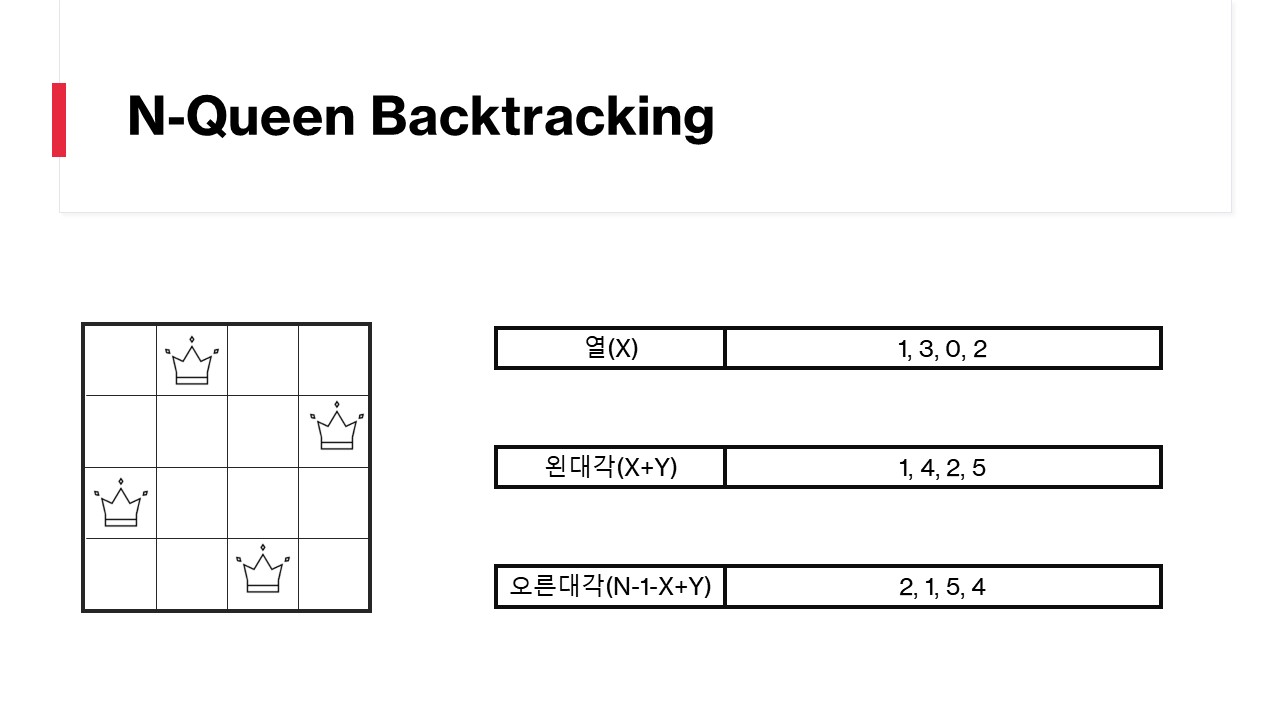
열 / 왼대각 / 오른대각에 들어있는 숫자들이 유일함을 확인할수있습니다.

N이 최대 15이므로 모든 가능한 가지수는 15!입니다. 1억을 훨씬 넘는 숫자이기 때문에 brute force로 안될것이라고 생각할수있지만, 가지치기(Pruning)를 통해 상당한 수의 가지수를 쳐내므로 brute force로 풀 수 있는 문제였습니다.

코드

'''
Created by jun on 21/05/26
N = int(input())
col = set()
#row = set()
ldiag = set()
rdiag = set()

def dfs(y:int)->int:
    if y == N:
        return 1

    res = 0
    for x in range(0, N):
    	#현재 위치에 해당하는 번호가 3개의 판에 있지 않은 경우
        if x not in col and y + x not in ldiag and y + (N-x-1) not in rdiag:
        	#3개의 판에 번호들을 추가함.
            col.add(x)
            ldiag.add(y + x)
            rdiag.add(y + N - x - 1)
            #재귀 호출. 다음 행을 검사함.
            res += dfs(y+1)
            #검사가 끝났으면 성공/실패 여부 상관없이 다음 실행을 위해 추가되었던 번호들을 제거함
            col.remove(x)
            ldiag.remove(y + x)
            rdiag.remove(y + N - x - 1)
    return res

print(dfs(0))

새로 알게된 사실

체스판을 보는 3가지 관점.