스도쿠

문제

빈칸이 존재하는 스도쿠를 채우는 문제

풀이

N-Queen문제와 같은 문제이다. 다만 N-Queen에서 운영하는 세가지 판과 스도쿠에서 운용하는 세가지 판은 다른점이 있다. 스도쿠판을 다음과 같은 세가지 관점에서 바라본다.

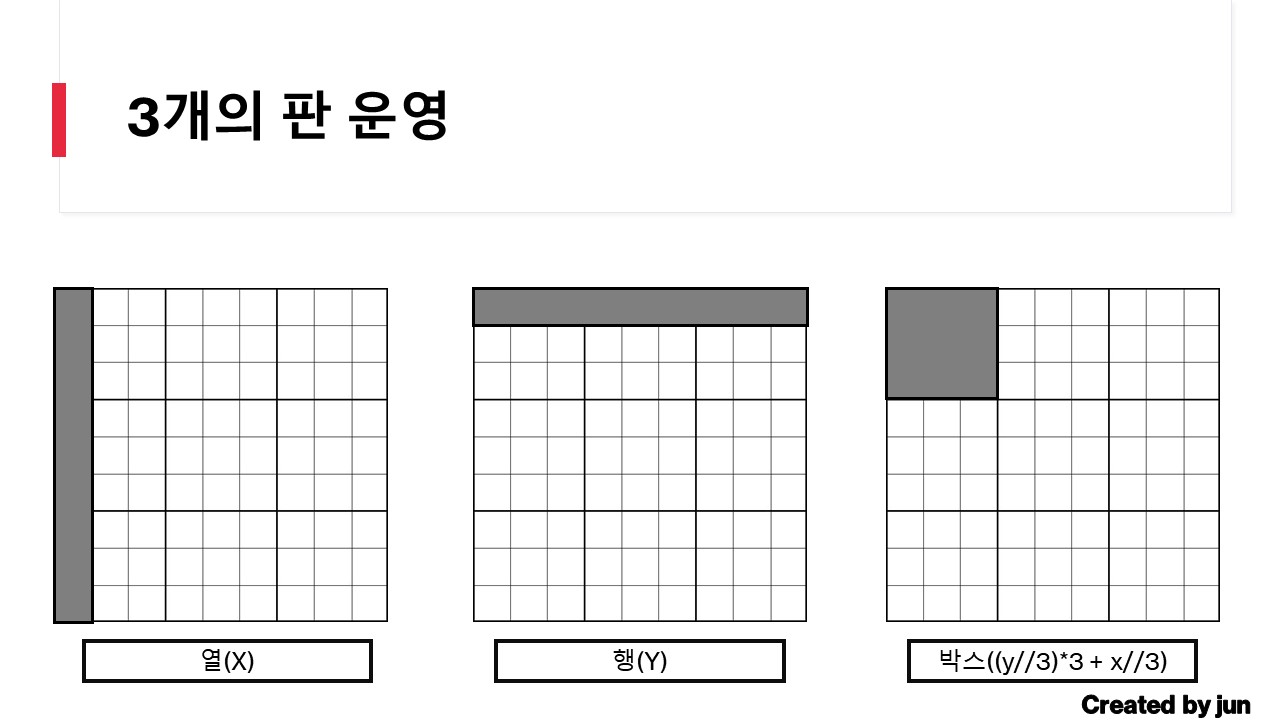
스도쿠를 더 이상 완성할수없는 가지에 대해 가지치기가 이루어지고 모든 정답의 수를 구하는것이 아닌 최초 발견한 정답의 수만 고려해서 프린트하기 때문에 가능한 모든 경우의 수가 1억을 넘어도 brute force로 풀수있는 문제였다.

• zero_list라는 리스트를 만들어서 빈칸 좌표를 모두 담고 zero_list에 들어있는 좌표에 대해서 스도쿠에 유효한 숫자를 넣는다.
  zero_list의 크기가 0일때까지 재귀가 이루어진다.

코드

'''
Created by jun on 21/05/27
'''
import collections
import sys

#주어진 board를 프린트합니다.
def print_board(board):
    for y in range(len(board)):
        for x in range(len(board[0])):
            print(board[y][x], end=" ")
        print()

#zero좌표를 모두 없애면 board를 print한다.
def dfs(zero_list, board):
    #zero좌표가 없으므로 완성된 board이다. print하고 종료한다.
    if len(zero_list) == 0:
        print_board(board)
        exit()

    #미완성된 board이다. 0을 채워야한다. 0에 대해서 유효한 경우 다음 재귀를 호출한다.
    ny, nx = zero_list[0]
    for N in range(1, 10):
        if N not in col_check[nx] and N not in row_check[ny] and N not in box_check[(ny//3)*3 + nx//3]:
            col_check[nx].add(N)
            row_check[ny].add(N)
            box_check[(ny//3)*3 + nx//3].add(N)
            board[ny][nx] = N
            dfs(zero_list[1:], board)
            board[ny][nx] = 0
            col_check[nx].remove(N)
            box_check[(ny // 3) * 3 + nx // 3].remove(N)
            row_check[ny].remove(N)


#입력 받는법?
board = [[int(x) for x in sys.stdin.readline().split()] for _ in range(9)]
zero_list = [(y, x) for x in range(len(board[0])) for y in range(len(board)) if board[y][x] == 0]

col_check = collections.defaultdict(set)
row_check = collections.defaultdict(set)
box_check = collections.defaultdict(set)

for y in range(len(board)):
    for x in range(len(board[0])):
        col_check[x].add(board[y][x])
        row_check[y].add(board[y][x])
        box_check[(y//3)*3 + x//3].add(board[y][x])

dfs(zero_list,board)

새로 알게된 사실

스도쿠판의 표현