1. Determinant and trace
2. Eigenvalues and Eigenvectors
3. Cholesky Decomposition
4. Eigendecomposition and Diagonalization
5. Singular Value DecompositionDeterminant and trace
Determinant의 개념
Determinant의 정의는 다음과 같이 나타낸다.
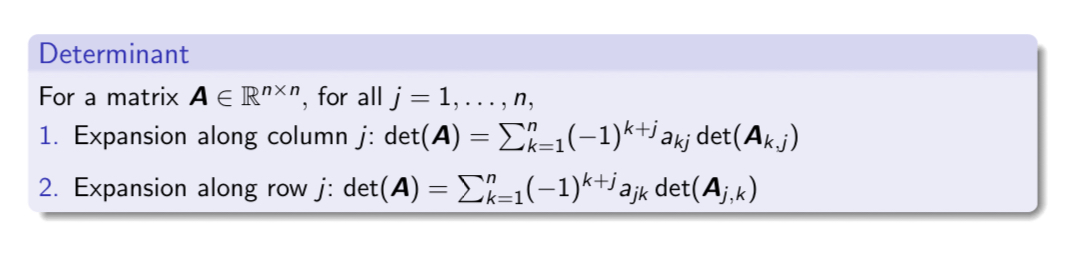
아래와 같이 3x3 Matrix의 Determinant를 2x2 Matrix의 Determinant로 다시 정의가 가능한데, 이를 Laplace expansion 라고 한다.

Determinant의 성질

여기에서 triangular matrix란 정방 매트릭스 내에서 대각선 요소 보다 우상방 경사방향 또는 좌하방 경사방향의 요소가 0이 되는 매트릭스를 말한다. 전자를 하삼각매트릭스, 후자를 상삼각매트릭스라고 한다.
trace의 개념
trace의 정의는 다음과 같이 나타낸다.
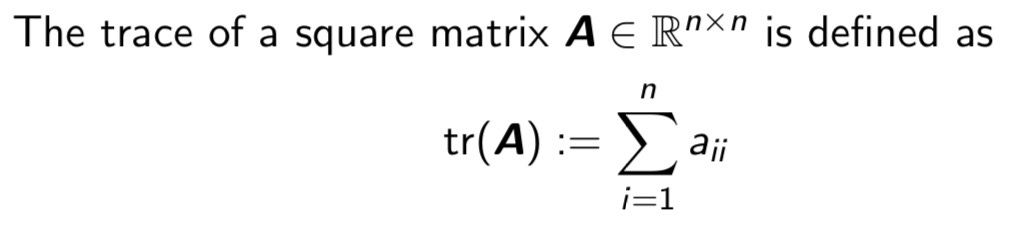
trace의 성질
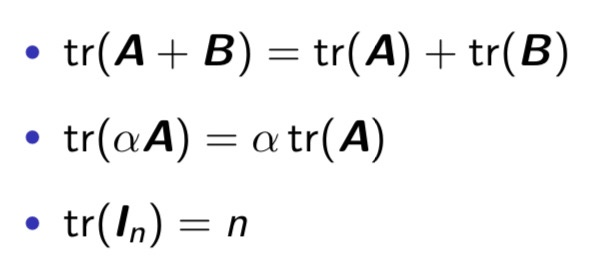
Eigenvalues and Eigenvectors
Ax = λx
Ax가 λx 라는 식으로 표현될 때 scaler value인 λ와 x vetor를 Eigenvalue와 Eigenvector라고 부른다. 어떤 Eigenvalue를 구하고 싶을 때, 아래의 방정식을 풀어 나오는 λ가 Eigenvalue가 된다.
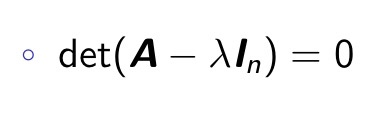
Eigenvalue들과 Determinant, Trace는 아주 밀접한 연관관계를 가진다. Determinant A는 Eigenvalue들의 곱셈으로 표현이 되며 Trace는 Eigenvalue들의 덧셈으로 표현이 된다. Eigenvalue를 계산하는 것은 Determinant를 계산하기 위한 방법 중 한 가지이다.

Cholesky Decomposition
행렬 A가 symmetric하고 모든 고유값(eigenvalue)들이 0보다 클 때는 행렬 A를 다음과 같이 나타낼 수 있다.
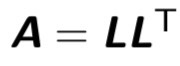
여기에서 L은 우상방 경사방향의 요소가 0이 되는 하삼각매트릭스를 뜻한다. Matrix L을 A의 Cholesky factor라고 한다.
Cholesky Decomposition을 하는 이유는?
Determinant의 성질에 의해 계산이 매우 쉬워지기 때문이다.
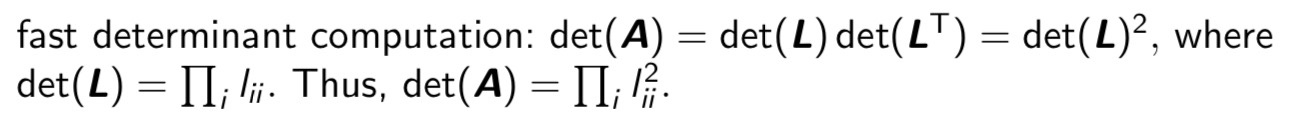
Eigendecomposition and Diagonalization
Diagonal matrix(대각선행렬)
다양한 연산들이 매우 쉽게 되는 성질이 있다.
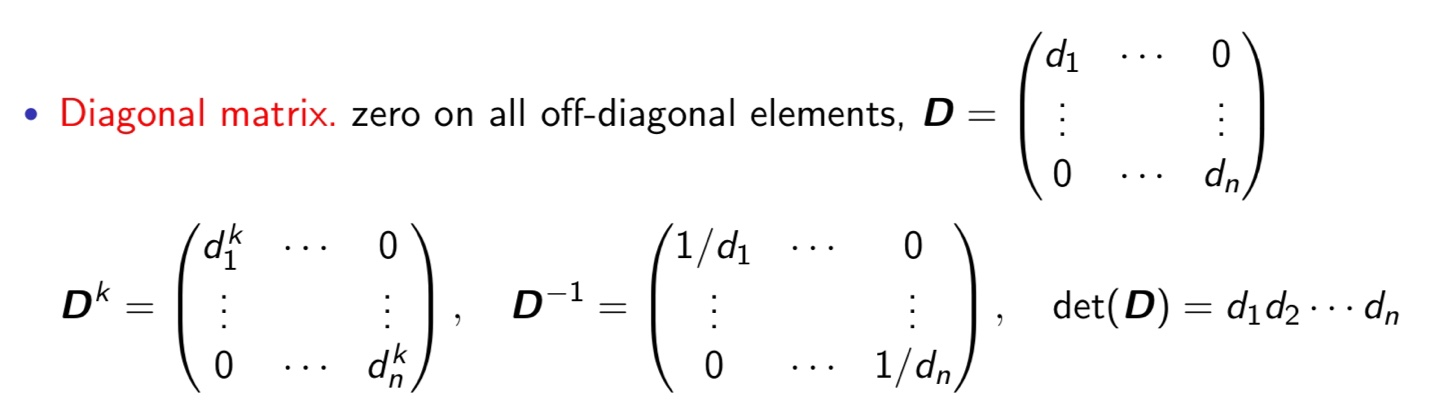
Diagonalizable 하게 되면 아래와 같은 단순한 형태로 표현이 된다.
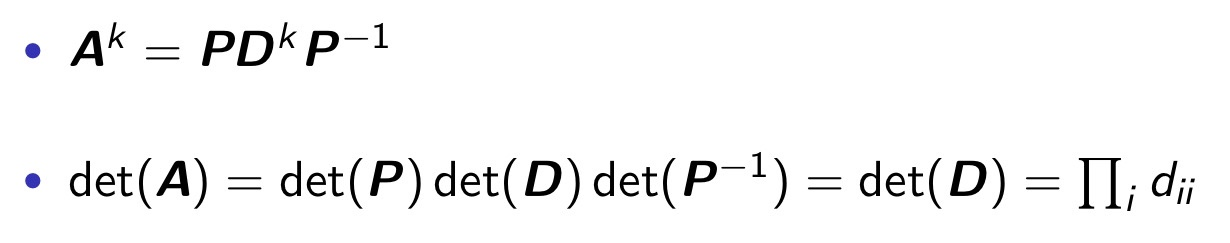
어떤 Matrix가 Diagonal하게 표현될 수 있을까?
A가 symmetric한 경우에는 항상 A가 Orthogonally Diagonalizible하다. 여기에서 P를 Eigenvector들을 모아놓은 Matrix, D를 Eigenvalue들을 모아놓은 Diagonal Matrix라고 정하면 아래와 같은 사실을 확인할 수 있다.

Singular Value Decomposition
Eigenvalue Decomposition은 symmetric matrix에만 적용할 수 있지만, singular value decomposition은 일반적인 matrix일 때, 즉 A가 symmetric 하지 않는 경우에 적용 가능하다. singular value decomposition은 항상 존재하기 때문에 더 유용하게 쓰인다.

여기에서 Σ의 Diagonal Entry를 singular value, matrix U를 구성하는 vector들을 singular vector, vector V를 구성하는 column vector들을 right singular vector 라고 부른다.
EVD vs. SVD
