[Algorithm] 이진 탐색(2)과 [백준 10816] 숫자 카드 2

6720·2023년 1월 18일

algorithm

이거 모르겠어요

목록 보기

5/38

다음 글과 이어짐

이진 탐색이 절반씩 좁혀가며 데이터를 탐색하는 방법인 것은 알겠지만 그렇다면 중복 원소의 개수를 구하려면 이진 탐색에서 어떤 식으로 변형해야 할까?

Lower bound와 Uppper bound

Lower bound: 하한 (찾고자 하는 값 이상의 값이 처음으로 나타나는 위치)
Upper bound: 상한 (찾고자 하는 값을 초과한 값이 처음으로 나타나는 위치)

흔히 경계를 의미하는 뜻에서 하계, 상계라고도 하며 이 값은 이번 이진 탐색의 핵심으로 사용됨.

EX) 배열 {1 3 4 4 4 5 5 6 6 6 7 9}가 있다고 하자
이 배열에서 4의 Lower bound와 Upper bound를 각각 구하라고 할 때 이는 2 5가 됨.

Lower bound는 찾고자 하는 값 이상의 값(= 4이상의 값)이 처음으로 나타나는 위치를 뜻하는데, 이는 4가 처음으로 나오는 인덱스 2를 뜻함.
Upper bound는 찾고자 하는 값을 초과한 값(= 4를 처음으로 넘는 값)이 처음으로 나타나는 위치라고 했는데 이는 4 다음에 5가 나오는 인덱스 5를 뜻함.

★ 이런 식으로 이진 탐색을 통해 하한선과 상한선을 구하여 범위만큼 카운팅하여 중복 원소의 개수를 구하라는 의미임.

EX2) 위와 똑같은 배열이 있다고 할 때, 8의 Lower bound와 Upper bound를 각각 구하시오.
배열에는 8이 존재하지 않음.

Lower bound: 8 이상의 값이 처음으로 나오는 인덱스 11
Upper bound: 8 초과의 값이 처음으로 나오는 인덱스 11

둘이 같아지게 됨.

★ 위의 예시와 지금의 내용을 합치면 Upper bound - Lower bound의 값이 중복 원소에 대한 길이가 되는데 이 예시는 11 - 11은 0이 되므로 중복 원소가 없음을 나타냄.

이진 탐색과 bound

그렇다면 이를 이진 탐색으로 어떻게 구할 수 있을까?
이진 탐색은 시작점과 끝점을 받아서 중간점과 원소의 크기 비교를 통해 시작점을 +1하고, 끝점을 -1하는 등의 조절로 원소의 존재를 판별함.

이와 비슷한 방법으로 Lower bound를 찾기 위해선 왼쪽으로 범위를 좁히고 Upper bound를 찾기 위해선 오른쪽으로 범위를 좁혀나가야 함.
왜냐하면 Lower bound는 이진 탐색에서의 시작점과 비슷한 의미를 가지고 있으며, Upper bound는 끝점과 비슷한 의미를 가지고 있기 때문.

EX) 배열 {1 3 4 4 4 5 5 6 6 6 7 9}가 있다고 하자
여기에서 4의 Lower bound와 Upper bound를 구해보자

[Lower bound]

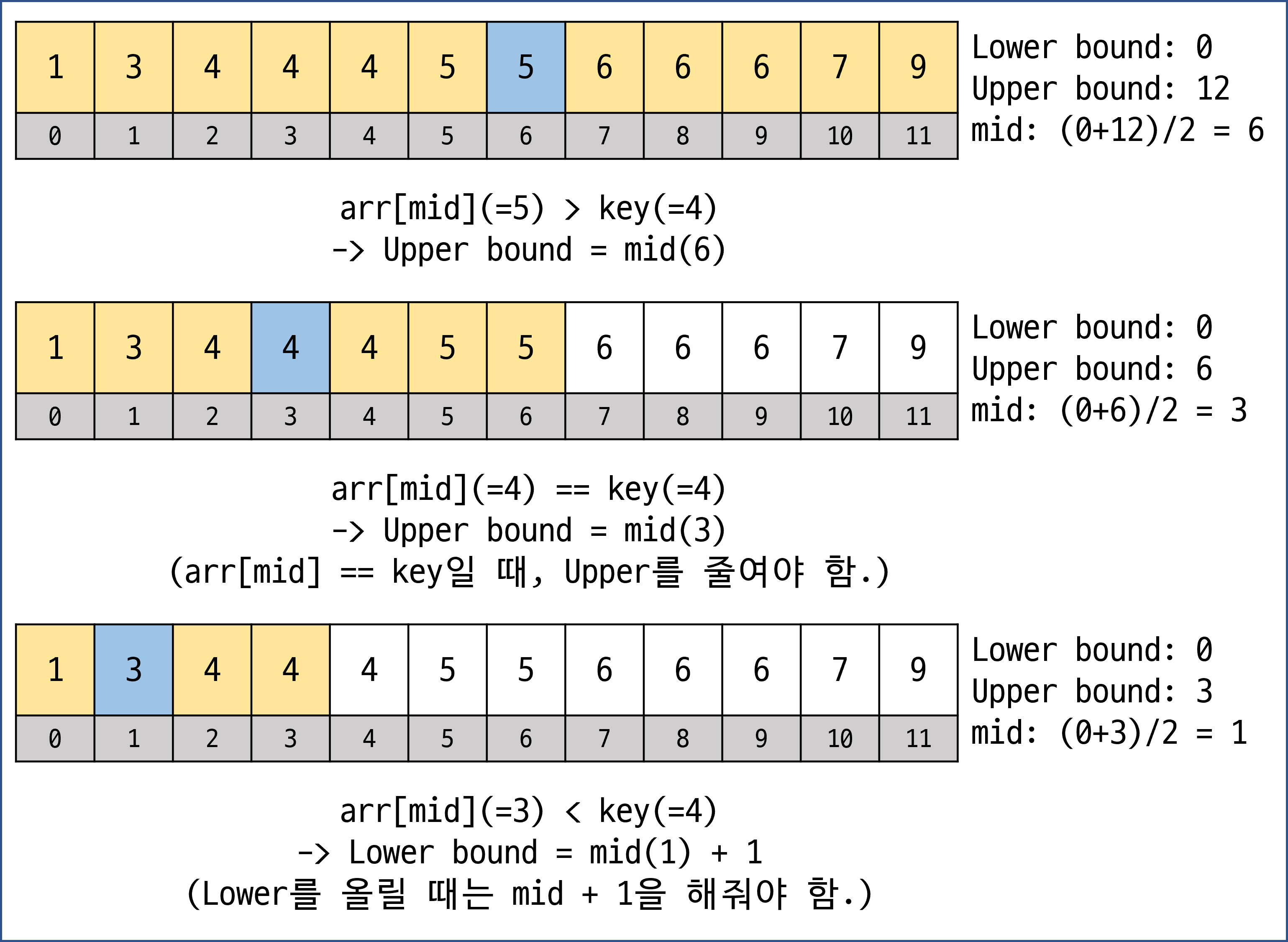
[Upper bound]

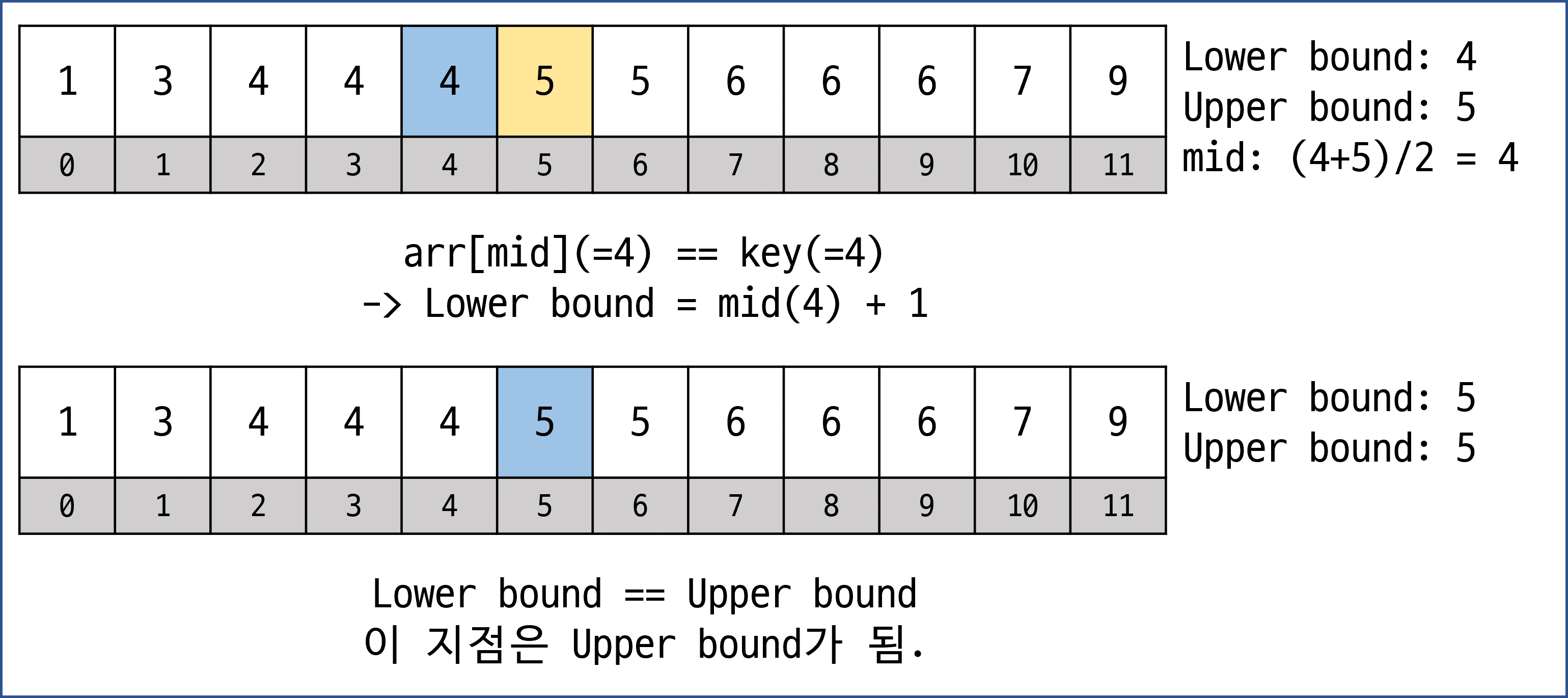
공식만 살짝 뽑아보면

Lower bound
- arr[mid] ≥ key: upper bound = mid
- arr[mid] < key: lower bound = mid + 1
Upper bound
- arr[mid] > key: upper bound = mid
- arr[mid] ≤ key: lower bound = mid + 1

가 될 것임.

[백준 10816] 숫자 카드 2

import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {

    static int[] arr;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int n = Integer.parseInt(br.readLine());
        arr = new int[n];
        StringTokenizer st = new StringTokenizer(br.readLine());
        for (int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }
        Arrays.sort(arr);

        int m = Integer.parseInt(br.readLine());
        st = new StringTokenizer(br.readLine());
        for (int i = 0 ; i < m; i++) {
            int key = Integer.parseInt(st.nextToken());
            bw.write(upper(key) - lower(key) + " ");
        }

        bw.flush();
        bw.close();
        br.close();
    }

    public static int lower(int key) {
        int lower_b = 0;
        int upper_b = arr.length;

        while (lower_b != upper_b) {
            int mid = (lower_b + upper_b) / 2;
            if (arr[mid] >= key) upper_b = mid;
            else lower_b = mid + 1;
        }
        return lower_b;
    }

    public static int upper(int key) {
        int lower_b = 0;
        int upper_b = arr.length;

        while (lower_b != upper_b) {
            int mid = (lower_b + upper_b) / 2;
            if (arr[mid] > key) upper_b = mid;
            else lower_b = mid + 1;
        }
        return upper_b;
    }
}