[Algorithm] 하노이 탑과 [백준 11729] 하노이 탑 이동 순서

하노이 탑

기둥이 3개일 때 모든 원판을 세번째 기둥에 그대로 옮기는 퍼즐임.
단, 규칙은 작은 원판 위에 그보다 크기가 큰 원판이 올라가면 안됨.

접근 방법(알고리즘)

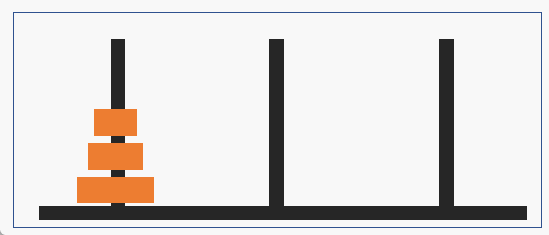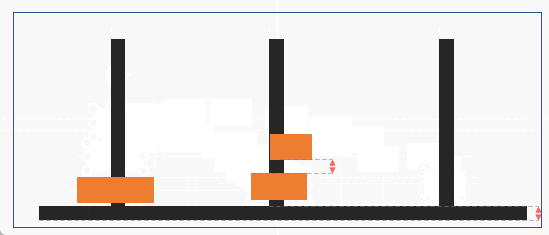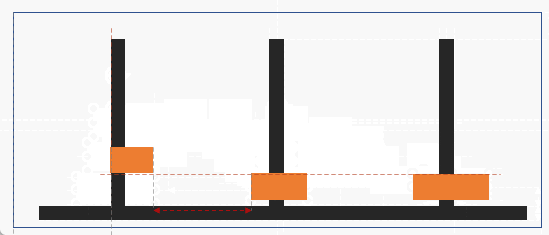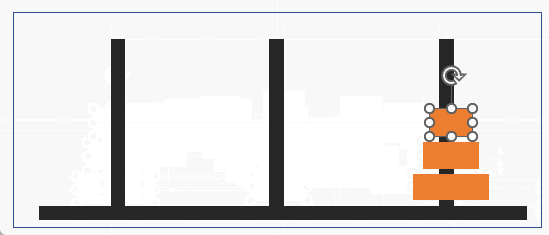
그렇다면 모든 판을 세번째 기둥에 옮기기 위해선 가장 먼저 해야할 것은 무엇일까?
그것은 가장 큰 원판을 먼저 바닥에 깔아두는 것임.

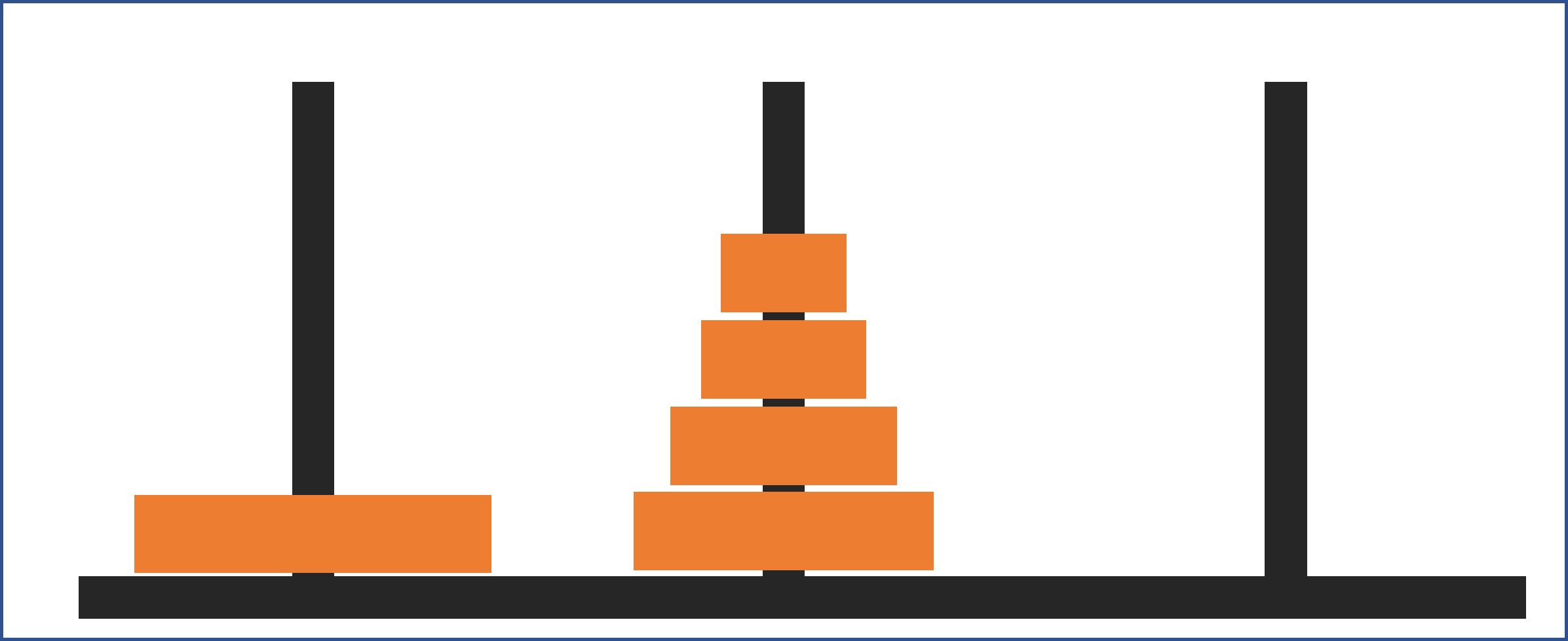
원판이 n개일 때 가장 큰 원판을 바닥에 깔기 위해선 나머지 n-1개의 원판이 두번째 기둥으로 옮겨져야 함.

그래야 마지막 원판이 이동할 수 있음.

그리고 나머지 n-1개 원판이 세번째 기둥으로 전부 이동하면 됨.
(첫번째 기둥에서 두번째 기둥으로 n-1개가 이동했던 것처럼 똑같이 해주면 됨.)
만약 이 이동 횟수를 카운팅해주는 함수 hanoi가 있다면 모든 원판을 옮기는 이동 횟수는
hanoi(n-1) + hanoi(1) (=1) + hanoi(n-1) 가 될 것임.
재귀를 사용해서 문제가 풀리게 될 텐데 결국 저 식은 hanoi(n)의 값이라고 볼 수도 있을 것임.

이를 귀납적으로 정리하게 되면 $a_{1} = 1, a_{n+1} = 2a_{n} + 1$가 됨.

양쪽에 +1을 해서 $a_{n+1} + 1 = 2(a_{n} + 1)$ 로 정리할 수 있고,

$b_{n} = a_{n} + 1$로 설정하여 $b_{n+1} = 2b_{n}$라는 식도 도출할 수 있음.

만약 n=1이라면 $b_{1} = a_{1} + 1 = 2$라는 결과가 나오는데, 이는 첫째항이 2이며 공비가 2인 공비수열임을 알 수 있음.

결론적으로 이를 이용하면

$b_{n} = a_{n} + 1 = 2^{n}$
$∴ a_{n} = 2^{n} - 1$
라는 결과가 나옴.

접근 방법(재귀)과 백준 11729 하노이 탑 이동순서

원판이 n개일 때 가장 큰 원판을 바닥에 깔기 위해선 나머지 n-1개의 원판이 두번째 기둥으로 옮겨져야 하는 것을 가져오면, 결국 두번째 기둥으로 옮겨지는 동작이 재귀로 동작되도록 해야함.

여기에서 n-1개가 이동하게 되면 나머지 1개의 가장 큰 원판은 세번째 기둥으로 옮겨지면 되므로 만약 원판이 1개가 남게 된다면 마무리되도록 설계되어야 할 것임.

if (n == 1) {
	return;
}

hanoi(n)가 2*hanoi(n-1) + 1이라고 했는데 그렇다면 n을 넣었을 때의 함수 안에서는 n-1로 재귀되는 과정이 있어야 할 것임.

void hanoi(int n) {
	if (n == 1) {
		return;
	}

	hanoi(n-1);
	hanoi(n-1);
}

여기서 문제를 다시 살펴볼 필요가 있음.

문제에서는 원판의 개수가 주어지면 그 원판의 개수의 이동횟수와 출발지점과 목적지점을 동시에 출력하라는 것을 확인할 수 있음.
기둥이 3개인 것이 고정일 때, hanoi의 필수 인자는 출발지점, 도착지점, 원판의 개수 가 될 것임.

void hanoi(int n, int from, int to) {
	if (n == 1) {
		System.out.println(from + " " + to);
		return;
	}

	hanoi(n-1, **, **);
	System.out.println(from + " " + to);
	hanoi(n-1, **, **);
}

• from과 to는 1, 2, 3 중 하나이며 이 둘 중 아무것도 아닌 기둥은 empty라고 칭함.

from과 to의 값을 기본적으로 받게될 때 empty의 값은 6 - from - to가 될 것임.
(기동이 1, 2, 3이고 다 더하면 6이기 때문)

하노이 탑이 모두 세번째 기둥으로 이동하는 조건을 다시 생각해보면

• 마지막 원판이 먼저 깔려야 할 것
• 그러기 위해선 n-1개의 원판이 두번째 기둥에 있어야 할 것
• 마지막 원판이 깔리면 n-1개의 원판이 세번째 기둥으로 와야 하는 것

이렇게 되는데 이는 이렇게 설계할 수 있음.

void hanoi(int n, int from, int to) {
	if (n == 1) {
		System.out.println(from + " " + to);
		return;
	}

	int empty = 6 - from - to;
	hanoi(n-1, from, empty);
	System.out.println(from + " " + to);
	hanoi(n-1, empty, to);
}

코드

import java.io.*;

public class Main {

    static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        bw.write((int)Math.pow(2, n) - 1 + "\n");
        hanoi(n, 1, 3);

        bw.flush();
        br.close();
        bw.close();
    }
    static void hanoi(int n, int from, int to) throws IOException {
        if (n == 1) {
            bw.write(from + " " + to + "\n");
            return;
        }

        int empty = 6 - from - to;
        hanoi(n-1, from, empty);
        bw.write(from + " " + to + "\n");
        hanoi(n-1, empty, to);
    }
}

bw를 전역에서 사용하고 싶으면 bw를 전역으로 내리고 사용하고 싶은 함수에 throws IOException을 붙이면 됨.

궁금증

• bw.write를 두군데에 놨는데 과연 겹치지 않는 걸까?

이를 확인하기 위해 bw.write에 n이 같이 출력되도록 함.

// 입력: 3
/* 출력 (from to n)
7
1 3 1
1 2 2
3 2 1
1 3 3
2 1 1
2 3 2
1 3 1
*/

음.. 겹치지는 않는데 과연 n과의 연관관계가 있나? 라고 물으면 그건 아닌거 같음.
그래서 hanoi를 손디버깅해보기로 함.

우선 동작 순서는 이렇게 됨.

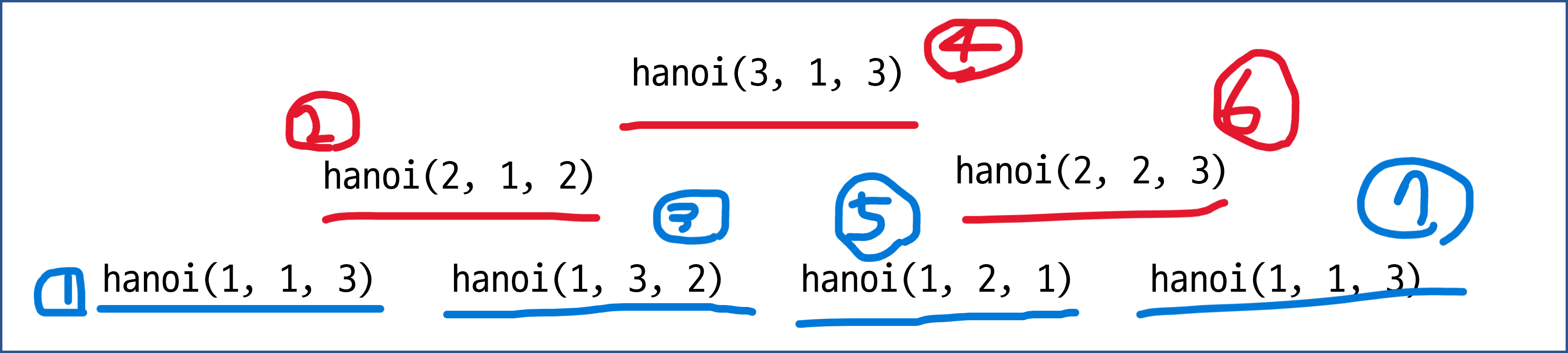
하지만 출력 순서는 이렇게 됐음.

파란색의 경우, n==1 if 문에서 출력되는 경우이며
빨간색의 경우, hanoi 사이에서 출력되는 경우임.
순서가 마치 중위 순회처럼 돌아감.

파란색의 경우 출력된 후 바로 마무리되어 hanoi 사이에서 출력이 겹칠까 했는데 애초에 출력하는 함수의 인자가 달랐기 때문에 걱정 안해도 되는 부분이었음.

후기

손디버깅할 때 뭐가 익숙한 그림이 나온다더니 오랜만에 보는 개념이 나왔다. 저거도 나중에 정리해둬야겠다.

개념 자체는 배우면 쉬운데 아무것도 모르는 상황에서 풀라고 하면 머리가 멈추는게 여러모로 아쉽다. 여러 문제에 있어서 접근하는 연습을 해봐야겠다.

참고 자료

• Stranger's LAB: 전반적인 풀이