병합(합병)정렬
폰 노이만*이 제안한 방법
일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬**에 속하며, 분할 정복 알고리즘***의 하나임.
[과정]
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 봄.
- 그렇지 않은 경우에는 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눔.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬함.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병함.
*존 폰 노이만(John von Neumann): 어디서 많이 들어본 사람이더니만 이산 구조, 이진법 등 컴퓨터 연구에도 힘쓴 사람이며, 2차 세계 대전과도 얽혀 있는 인물임.
**안정 정렬(stable sort): 중복된 값을 입력 순서와 동일하게 정렬하는 정렬 알고리즘 EX) 삽입정렬, 병합정렬, 버블정렬
(vs 불안정 정렬(unstable sort): 안정 정렬과 반대로 중복된 값이 입력 순서와 동일하지 않게 정렬되는 알고리즘 EX) 퀵정렬, 선택정렬, 계수정렬)
***분할 정복(Divide and Conquer) 알고리즘: 문제를 작은 2개의 문제로 분리하고 각각 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이며 대개 순환 호출을 이용하여 구현함.
구체적인 개념
하나의 리스트를 두 개의 균등한 크기로 분할하고, 분할된 부분 리스트를 정렬함.
두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법.
[단계]
- 분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할함.
- 정복(Conquer): 부분 배열을 정렬함. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법 적용함.
- 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병함.
[과정]
- 추가적인 리스트 필요함.
- 각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용함.
- 합병 정렬에서 실제로 정렬이 이루어지는 시점은 2개의 리스트를 결합하는 단계임.
장단점
[장점]
- 안정적인 정렬 방법: 데이터의 분포에 영향을 덜 받음. → 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일함. (
O(nlog₂n)) - 만약 레코드를 연결 리스트*로 구성한다면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아짐. (제자리 정렬**로 구현할 수 있음.)
→ 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 다른 어떤 정렬 방법보다 효율적임.
[단점]
- 만약 레코드를 배열로 구성한다면, 임시 배열이 필요함. (제자리 정렬이 아님)
- 레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래함.
*연결 리스트(Linked List): 각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 방식으로 데이터를 저장하는 자료 구조
데이터를 담고 있는 노드들이 연결되어 있는데, 노드의 포인터가 다음이나 이전의 노드와의 연결을 담당하게 됨.
**제자리 정렬(in-place sorting): 원소들의 개에 비해서 충분히 무시할 만한 저장 공간만을 더 사용하는 정렬 알고리즘.
EX) 삽입 정렬: 이미 주어진 원소들을 옮긴 뒤 적절한 위치에 원소를 삽입하는 연산을 반복하는 데, 이 과정에서 원소들을 담는 공간 외에 추가로 사용될 수 있는 공간은 옮겨지는 원소가 저장되는 공간과 루프 변수 정도에 불과함.
Example
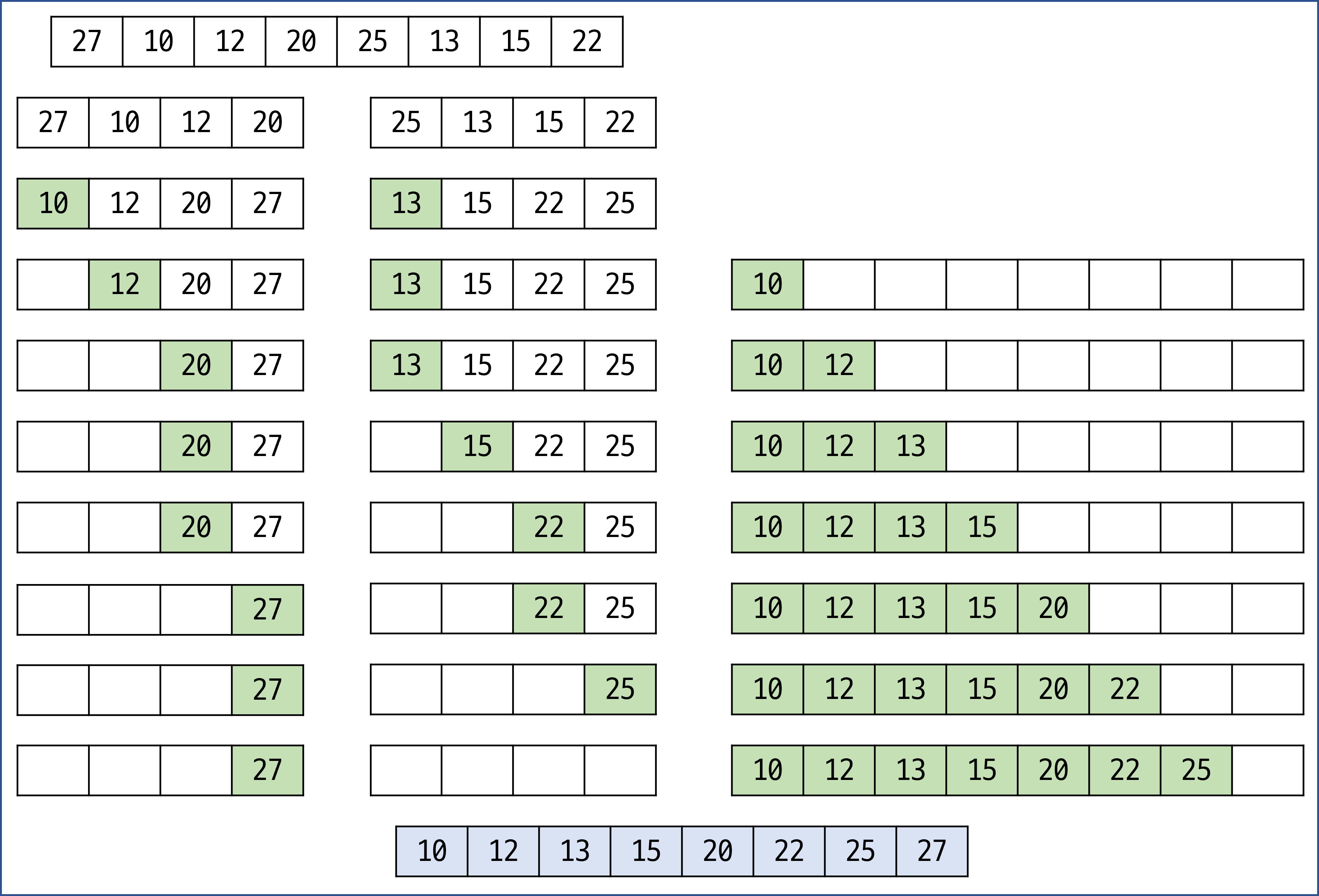
배열에 27, 10, 12, 20, 25, 13, 15, 22이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
- 2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 개의 리스트의 값 중에서 더 작은 값을 새로운 리스트로 옮김.
- 둘 중 하나가 끝날 때까지 이 과정을 되풀이함.
- 만약 둘 중 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 값들을 전부 새로운 리스트로 복사함.
- 새로운 리스트를 원래의 리스트로 옮김.
[코드]
import java.io.*;
public class Main {
public static int[] sorted = new int[8];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = 8;
int[] list = {27, 10, 12, 20, 25, 13, 15, 22};
merge_sort(list, 0, n-1);
for (int i = 0; i < n; i++) {
bw.write(list[i] + " ");
}
bw.flush();
br.close();
bw.close();
}
public static void merge(int list[], int left, int mid, int right) {
int i = left;
int j = mid+1;
int k = left;
while (i <= mid && j <= right) {
if (list[i] <= list[j]) sorted[k++] = list[i++];
else sorted[k++] = list[j++];
}
if (i > mid) {
for (int l = j; l <= right; l++) sorted[k++] = list[l];
} else {
for (int l = i; l <= mid; l++) sorted[k++] = list[l];
}
for (int l = left; l <= right; l++) list[l] = sorted[l];
}
public static void merge_sort(int list[], int left, int right) {
int mid;
if (left < right) {
mid = (left + right) / 2;
merge_sort(list, left, mid);
merge_sort(list, mid + 1, right);
merge(list, left, mid, right);
}
}
}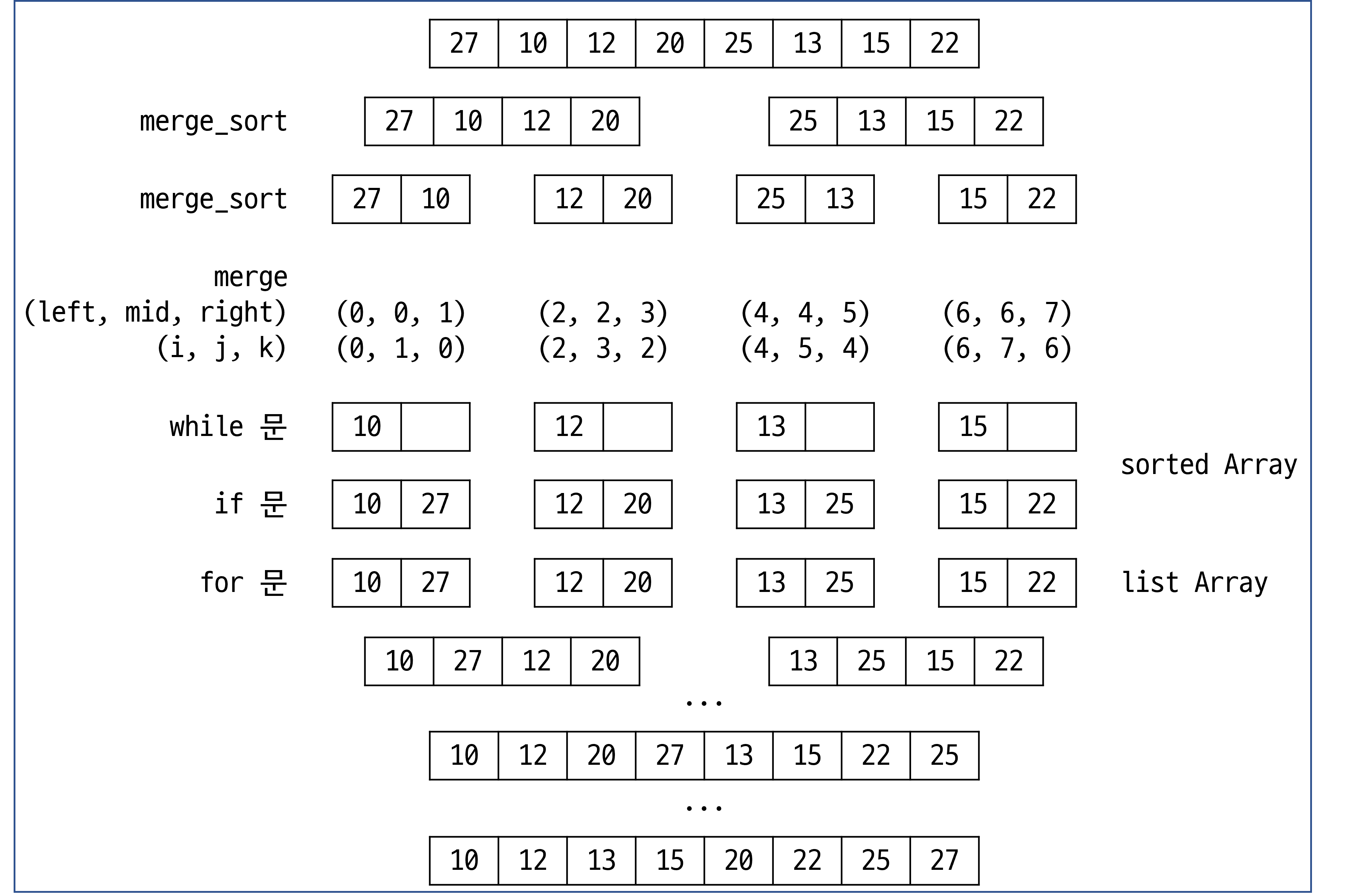
merge_sort(0, 7)안에merge_sort(0, 3)와merge_sort(4, 7)가 포함되어 있음.merge_sort(0, 3)안에merge_sort(0, 1)와merge_sort(2, 3)가 포함되어 있음.merge_sort(4, 7)안에merge_sort(4, 5)와merge_sort(6, 7)가 포함되어 있음.
이 글의 목적(백준 24060 알고리즘 수업 - 병합 정렬 1)
이 문제를 풀기위해선 한 가지 지식이 더 필요함.
이 문제에서는 결과를 도출하기 위해 저장 횟수와 k를 비교하는 것을 요구함.
그렇다면 저장 횟수를 어떤 구문이 실행될 때 카운팅되도록 해야할까?
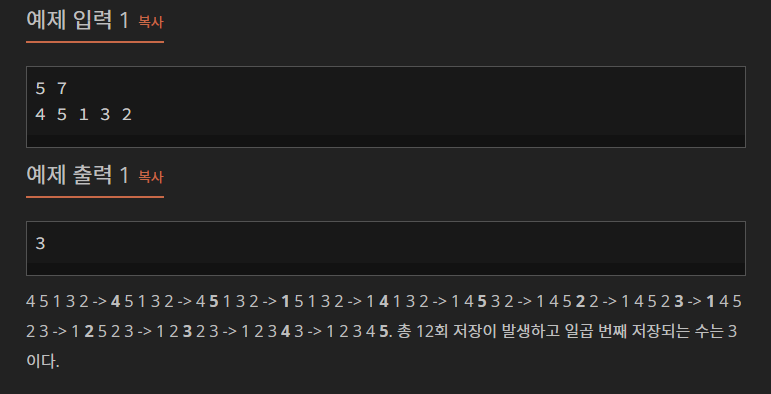
예제에 풀이가 나오는데 이를 살펴볼 필요가 있음.

merge_sort(0, 4)안어merge_sort(0, 2)와merge_sort(3, 4)가 포함되어 있음.merge_sort(0, 2)안어merge_sort(0, 1)와merge_sort(2, 2)가 포함되어 있음.
만약 코드가 실행되면 merge_sort의 실행은 merge_sort(0,1) → merge_sort(2, 2) → merge_sort(0, 2) → merge_sort(3, 4) → merge_sort(0, 4) 순서로 실행될 것이고 merge() 또한 이 순서대로 실행될 것 임.
⇒ 결론적으로 merge 함수에서의 for 문에서 list 배열로 값이 저장될 때마다 저장 횟수가 카운팅 될 것임. (예제 풀이애서 배열 한 칸 씩 값이 변하고 있으므로)
이제 저장 횟수에 대한 저장된 값을 어떻게 가지고 오냐만 남았음.
조건에 저장 횟수가 k보다 작으면 -1을 출력하는 것이 있으므로 총 저장 횟수가 필요할 것이며, 저장 횟수에 따른 저장된 값 또한 필요할 것임. → 이는 해시맵 사용.
[코드]
import java.io.*;
import java.util.*;
public class Main {
public static int[] sorted = {};
public static HashMap<Integer, Integer> count = new HashMap<Integer, Integer>();
public static int index = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int[] list = new int[n];
sorted = new int[n];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
list[i] = Integer.parseInt(st.nextToken());
}
merge_sort(list, 0, n-1); // list 분할
if (count.size() >= k) bw.write( count.get(k-1) + "");
else bw.write(-1 + "");
bw.flush();
br.close();
bw.close();
}
public static void merge(int list[], int left, int mid, int right) {
int i = left;
int j = mid+1;
int k = left;
while (i <= mid && j <= right) {
if (list[i] <= list[j]) sorted[k++] = list[i++];
else sorted[k++] = list[j++];
}
if (i > mid) {
for (int l = j; l <= right; l++) sorted[k++] = list[l];
} else {
for (int l = i; l <= mid; l++) sorted[k++] = list[l];
}
for (int l = left; l <= right; l++) {
list[l] = sorted[l];
count.put(index++, sorted[l]);
}
}
public static void merge_sort(int list[], int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
merge_sort(list, left, mid); // list 분할 (왼쪽)
merge_sort(list, mid + 1, right); // list 분할 (오른쪽)
merge(list, left, mid, right); // list 정렬
}
}
}[주의]
이 문제는 시간 제한이 있기 때문에 비교적 크기가 큰 경우에는 전부 전역 변수로 빼야 함.
후기
카페모카 마시고 하니깐 귀막히고 눈 따갑고 헛구역질 나오는 상황에서 하는 알고리즘 공부는 좋은 선택은 아닌 것 같다
하필 오늘 이렇게 어려운거 걸려가지고..
참고 자료
- Heee’s Development Blog: 합병 정렬 관련
- 홍러닝: 안정 정렬과 불안정 정렬
- 나무위키: 분할 정복 알고리즘
- 위키피디아1: 연결 리스트
- 위키피디아2: 정렬 알고리즘