
1. 다익스트라 알고리즘
1-1. 개요
다익스트라(dijkstra) 알고리즘은 그래프에서 한 정점(노드)에서 다른 정점까지의 최단 경로를 구하는 알고리즘 중 하나이다. 이 과정에서 도착 정점 뿐만 아니라 모든 다른 정점까지 최단 경로로 방문하며 각 정점까지의 최단 경로를 모두 찾게 된다. 매번 최단 경로의 정점을 선택해 탐색을 반복하는 것이다.
참고로 그래프 알고리즘 중 최소 비용을 구하는 데는 다익스트라 알고리즘 외에도 벨만-포드 알고리즘, 프로이드 워샬 알고리즘 등이 있다.
1-2. 동작 단계
① 출발 노드와 도착 노드를 설정한다.
② '최단 거리 테이블'을 초기화한다.
③ 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고, 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택한다. 그 노드를 방문 처리한다.
④ 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(가중치)을 계산해 '최단 거리 테이블'을 업데이트한다.
⑤ ③~④의 과정을 반복한다.
'최단 거리 테이블'은 1차원 배열로, N개 노드까지 오는 데 필요한 최단 거리를 기록한다. N개(1부터 시작하는 노드 번호와 일치시키려면 N + 1개) 크기의 배열을 선언하고 큰 값을 넣어 초기화시킨다.
'노드 방문 여부 체크 배열'은 방문한 노드인지 아닌지 기록하기 위한 배열로, 크기는 '최단 거리 테이블'과 같다. 기본적으로는 False로 초기화하여 방문하지 않았음을 명시한다.
1-3. 동작 예
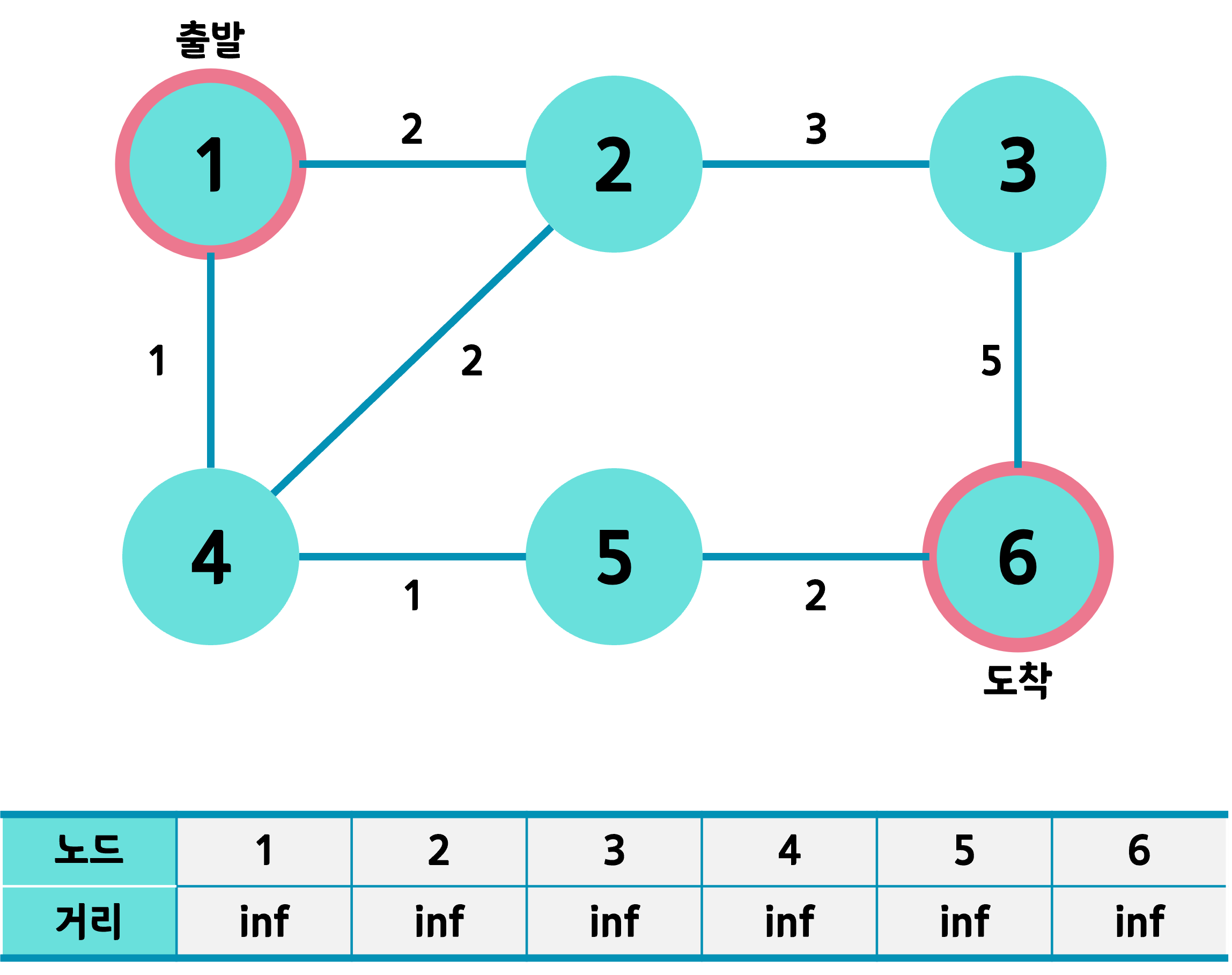
출발 노드는 1번, 도착 노드는 6번이라 하고 거리 테이블을 전부 큰 값, 여기서는 inf(무한대)로 초기화했다. 각 노드들을 잇는 간선의 가중치 역시 표시했다.
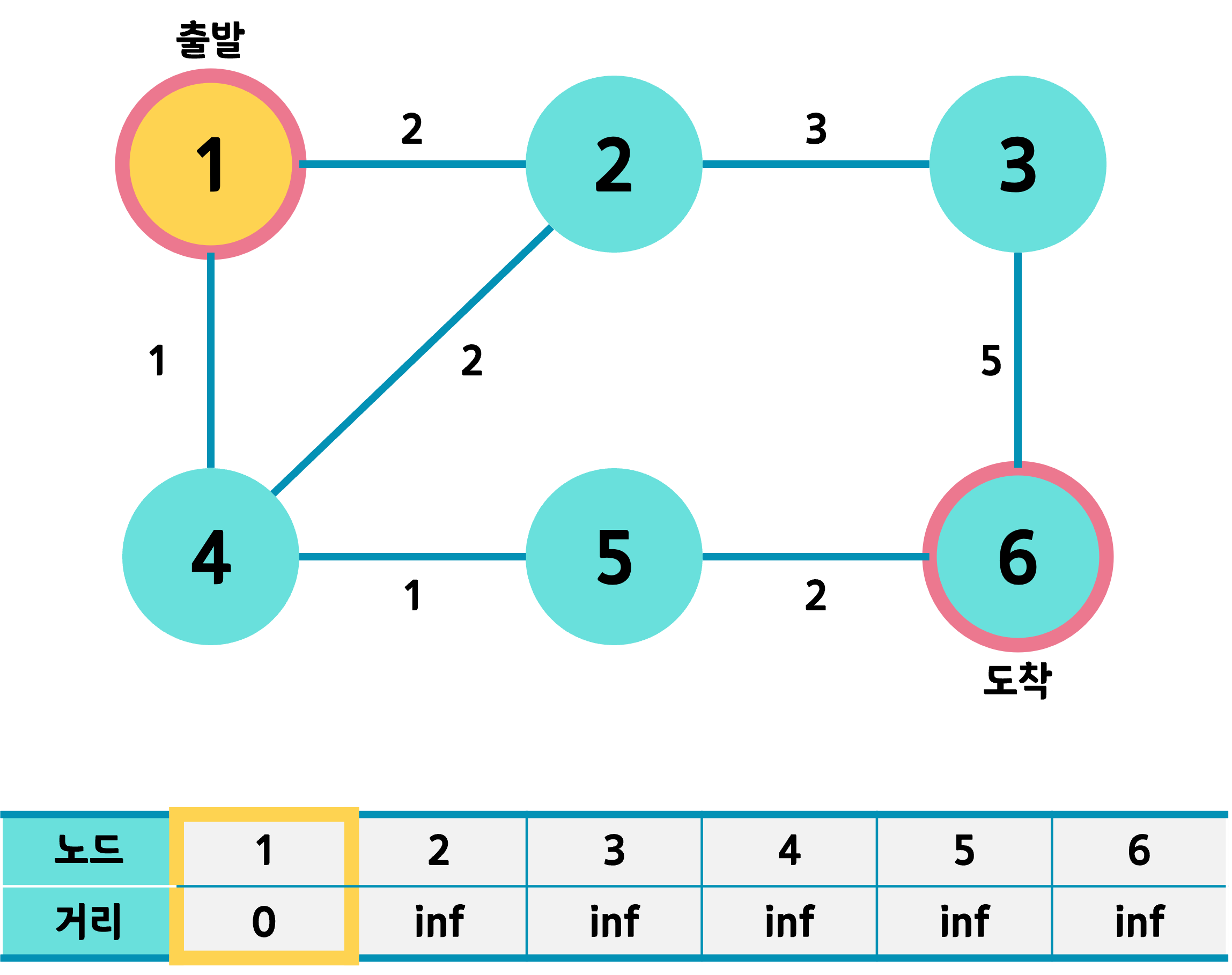
출발 노드를 먼저 선택하고 거리를 0으로 한다.
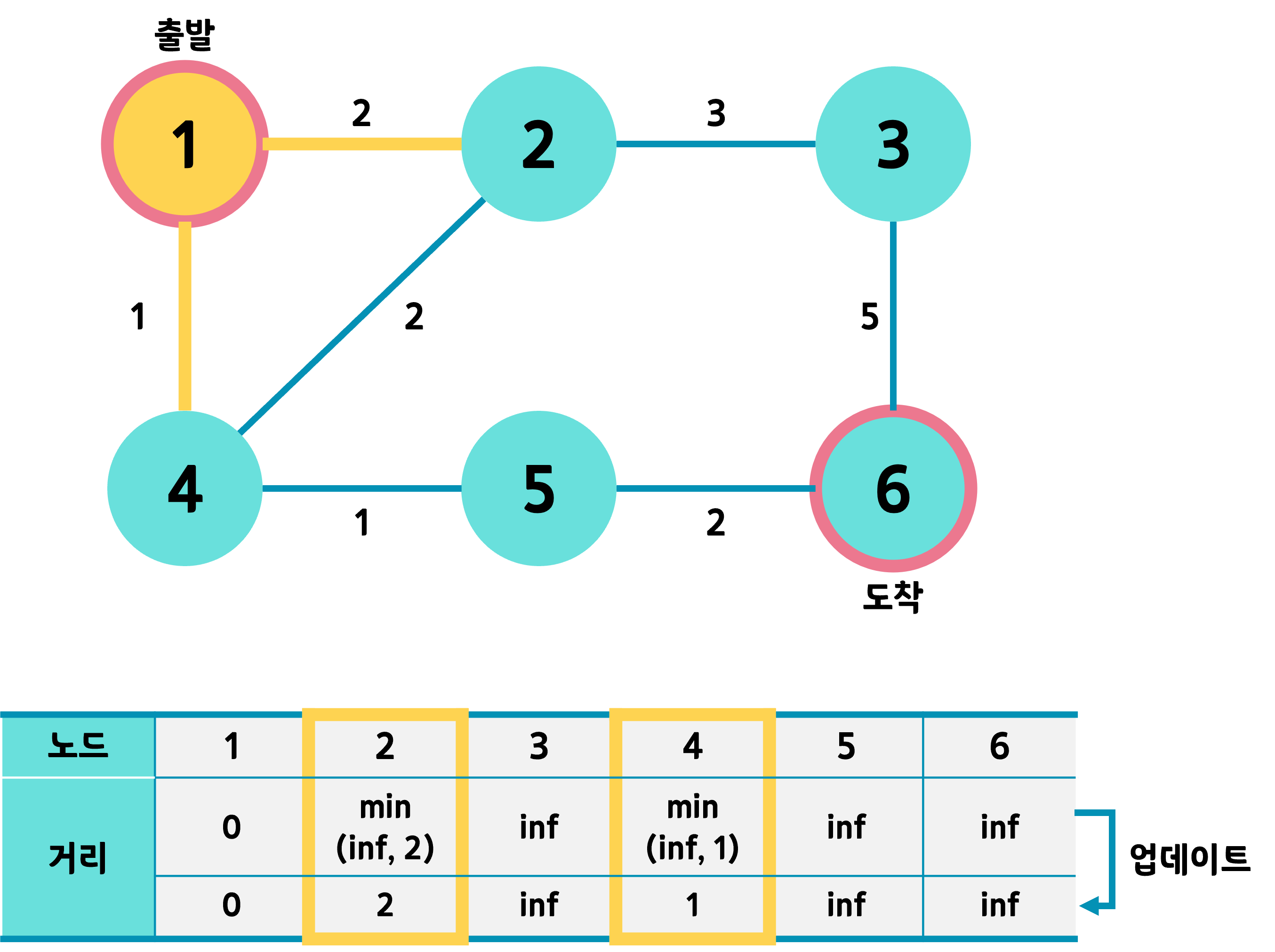
1번 노드와 연결된 인접 노드는 2, 4이다. 그곳까지 가는 거리를 각각 기존의 거리값과 비교해 최솟값으로 업데이트한다. 가령 2의 경우 inf와 2 중 작은 값인 2를 택해 할당한다.
또한 인접 노드까지의 거리를 모두 업데이트한 1번 노드는 방문 표시를 한다.
최근 갱신한 테이블 기준, 방문하지 않는 노드 중 가장 거리값이 작은 번호를 다음 노드로 택한다. 위 상태에서는 4번 노드이다.
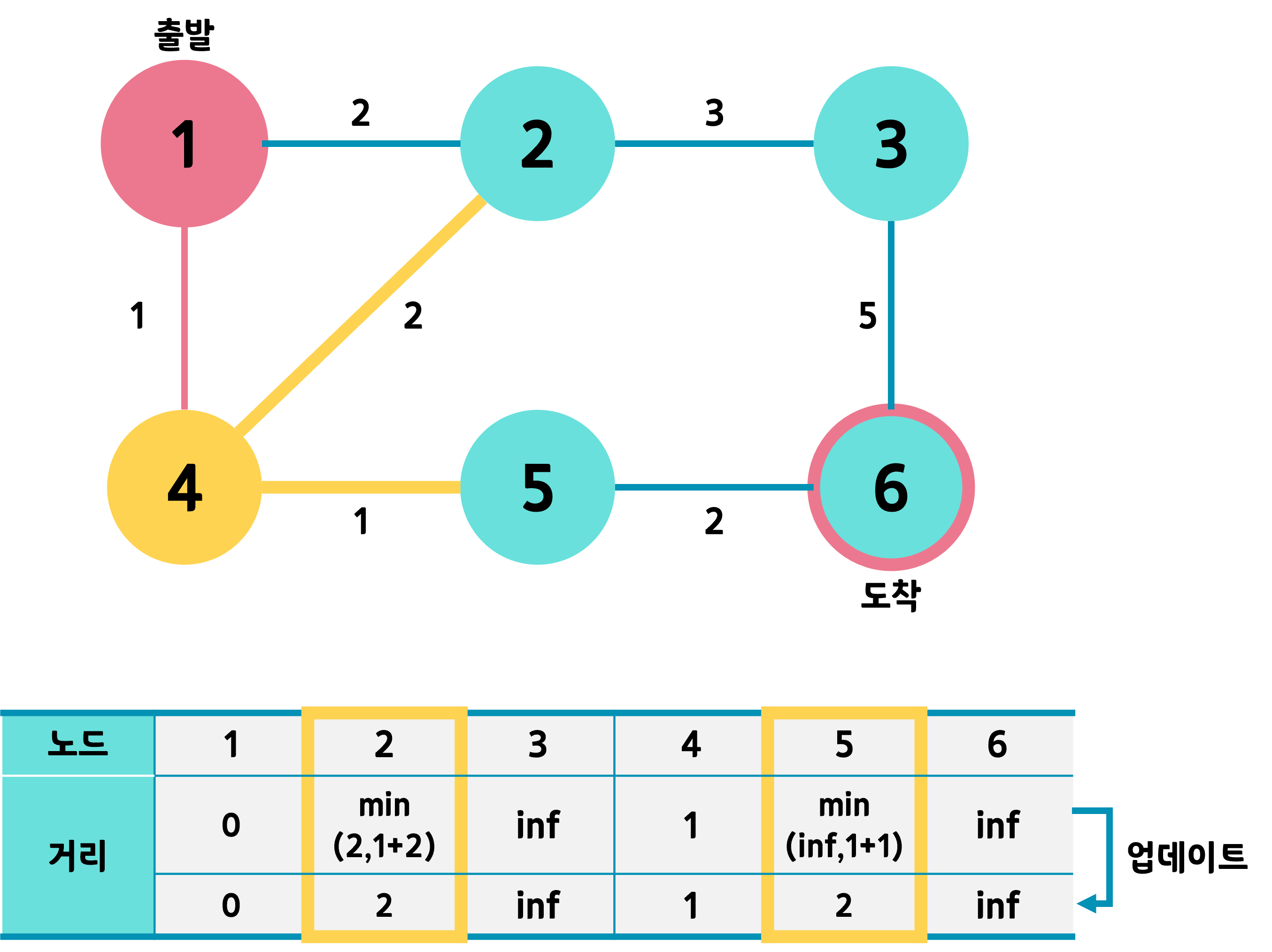
4번 노드에서 같은 작업을 수행한다. 4번과 연결된 2, 5번까지 오는 거리를 계산한다. 가령 5의 경우엔 4번까지 오는 데 필요한 거리 + 4->5 간선의 가중치 값인 2와 기존의 값인 inf 중 최솟값을 계산하고, 2번 노드의 경우엔 기존 값인 2와 4번을 거쳐가는 값인 1+2 = 3을 비교한다. 그렇다면 2번 노드는 기존 값이 더 크므로 업데이트하지 않는다. 즉, 1번에서 바로 2번으로 가는 것이 1->4를 거쳐 2번으로 가는 길보다 더 적게 걸린단 뜻이다.
다음으로 선택될 노드는 아직 방문하지 않은 노드 2, 3, 5, 6 중 거리값이 가장 작은 노드이므로 2 또는 5이다. 거리 값이 같다면 일단 인덱스가 작은 노드를 택한다고 하고 2번으로 가보자.

2번 노드와 연결된 3, 4번 노드에 대해 같은 과정을 반복한다.
그 다음 노드는 3, 5, 6번 중 가장 거리값이 작은 5번 노드가 되겠다.
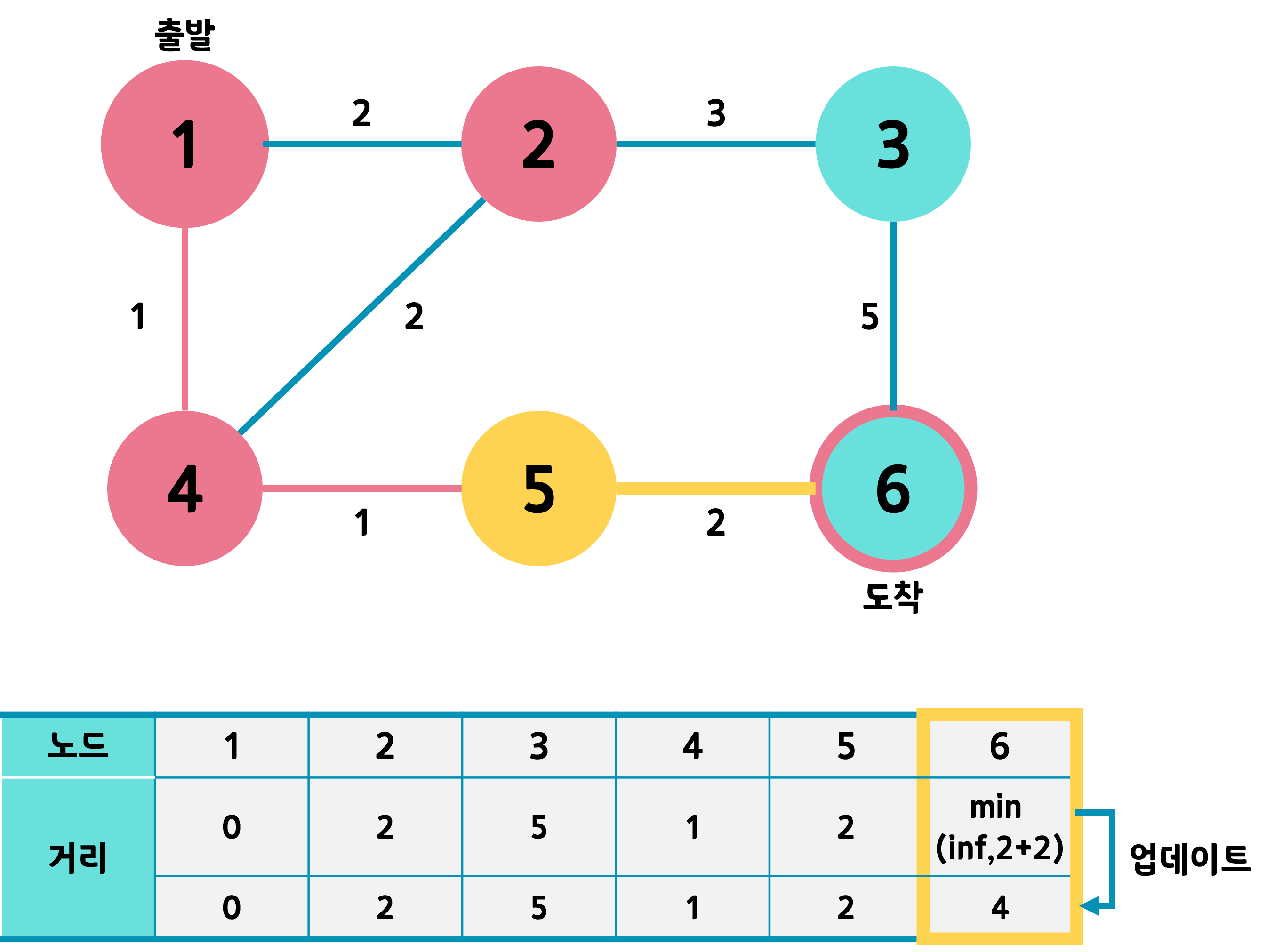
5번 노드와 연결된 6번 노드에 같은 과정을 반복한다.
다음 노드를 선택해야 하는데, 아직 방문하지 않은 3번과 6번 중 거리값이 작은 것은 6번이다. 그런데 6번은 더 이어지는 노드도 없는데다 도착 노드이다. 따라서 알고리즘을 종료한다.
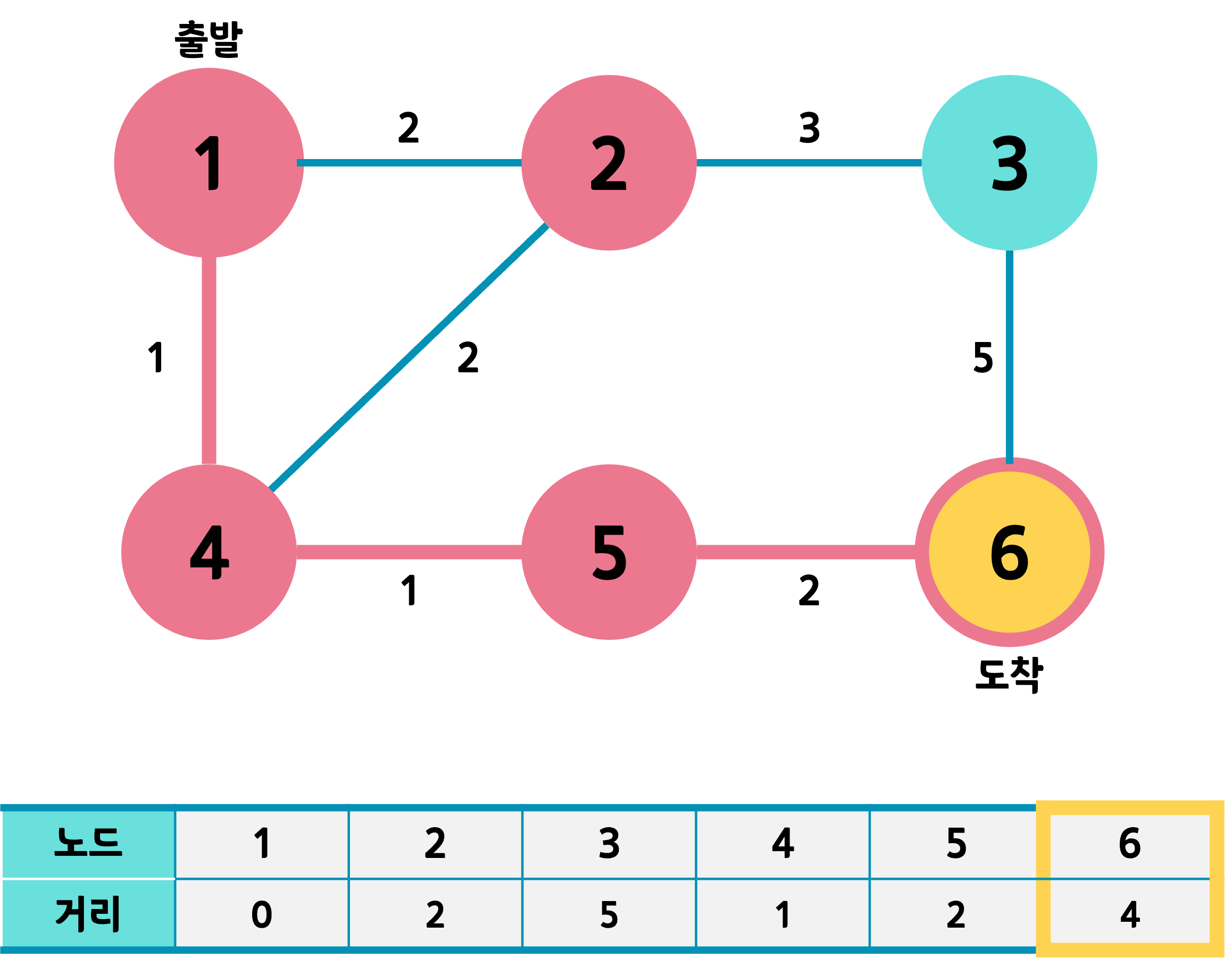
최종적으로는 1번에서 6번까지 오는 데 1 - 4 - 5 - 6의 경로를 거치고 최소 거리는 4가 된다.
1-4. 특징
위 동작 예시에서 볼 수 있듯이, 다익스트라 알고리즘은 방문하지 않은 노드 중 최단 거리인 노드를 선택하는 과정을 반복한다.
또한 각 단계마다 탐색 노드로 한 번 선택된 노드는 최단 거리를 갱신하고, 그 뒤에는 더 작은 값으로 다시 갱신되지 않는다.
도착 노드는 해당 노드를 거쳐 다른 노드로 가는 길을 찾을 필요는 없다.
다익스트라 알고리즘은 가중치가 양수일 때만 사용 가능하다는 중요한 특징이 있다.
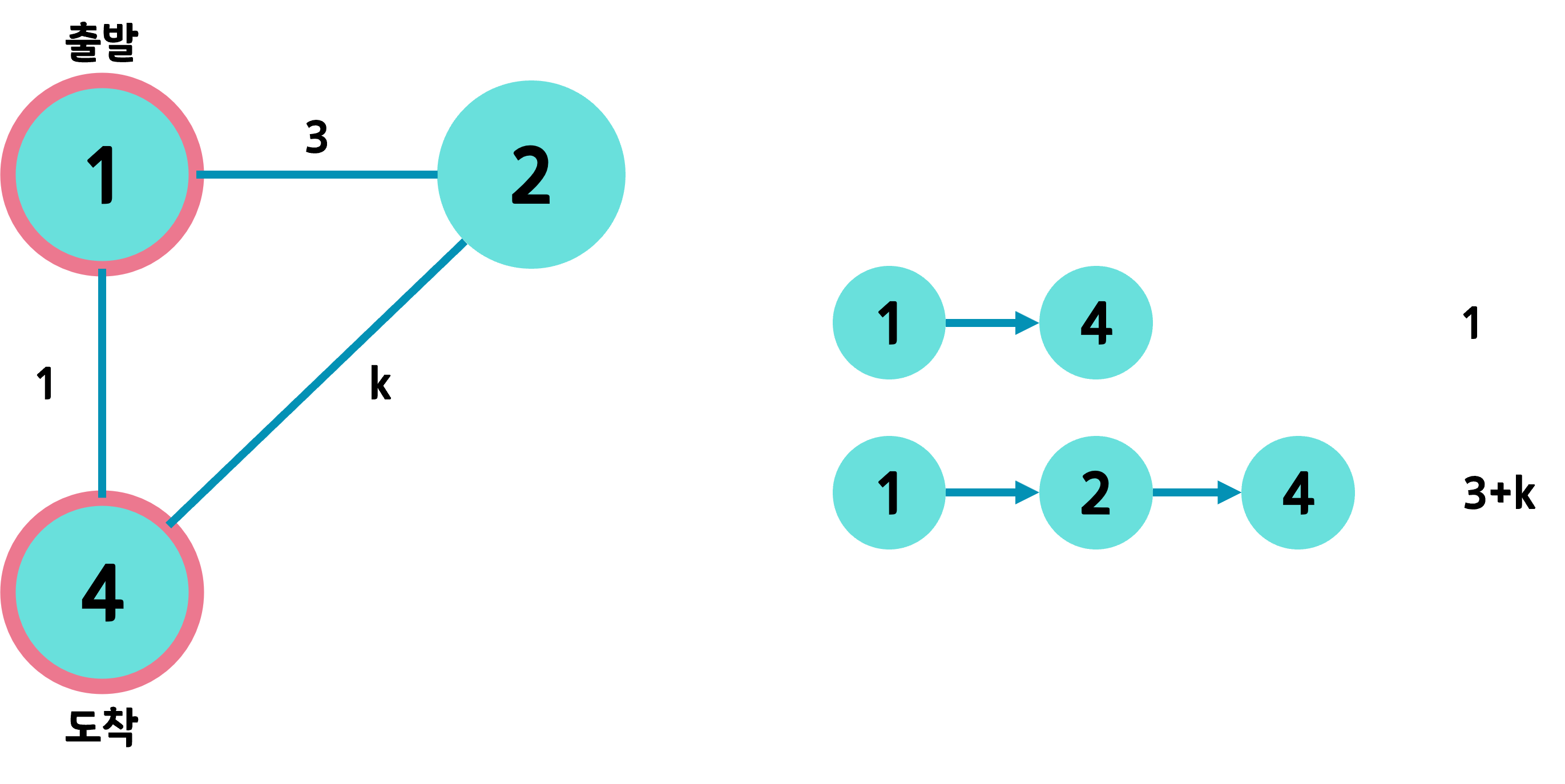
위 그림의 상황에서 1 → 4의 경로가 최단경로이려면 3+k가 1보다 커야 한다. 즉, k > -2가 성립해야 한다. 반대로 k가 -5라고 한다면 오히려 1 → 2 → 4 경로가 더 최단 경로가 된다. 그 말인 즉, 1번에서 연결된 노드 중 4번이 가중치가 적다는 이유로 최단 거리를 1이라 할 수는 없다는 이야기이다.
따라서 다익스트라 알고리즘을 사용하기 위해서는 정점 사이를 잇는 간선의 가중치가 양수여야 한다. 그래야 한 번 방문한 정점에 대해서는 값을 업데이트 하지 않아도 되는 것이다.
1-5. 구현 방법
다익스트라 알고리즘을 구현하는 방법에는 '방문하지 않은 노드'를 다루는 방식에서 '순차 탐색'을 할 것이나 '우선순위 큐'를 쓸 것이냐로 나뉜다. 자세한 방식은 아래에서 계속한다.
2. 구현(1): 순차 탐색
'방문하지 않은 노드 중 거리값이 가장 작은 노드'를 선택해 다음 탐색 노드로 삼는다. 그 노드를 찾는 방식이 순차 탐색이 된다. 즉 거리 테이블의 앞에서부터 찾아내야 하므로 노드의 개수만큼 순차 탐색을 수행해야 한다. 따라서 노드 개수가 N이라고 할 때 각 노드마다 최소 거리값을 갖는 노드를 선택해야 하는 순차 탐색이 수행되므로 의 시간이 걸린다.
아래 코드에서 dist[]는 각 노드까지의 최소 거리를 저저장하고, visited[]는 방문 여부를, map[][]은 한 노드에서 다른 노드로의 거리를 저장하고 있다.
#include <vector>
#include <queue>
// 아직 방문하지 않은 노드 중
// 가장 거리값이 작은 노드의 인덱스 반환
int FindSmallestNode()
{
int min_dist = INF;
int min_idx = -1;
for (int i = 0; i<= N; i++)
{
if (visited[i] == true)
continue;
if (dist[i] < min_dist)
{
min_dist = dist[i];
min_idx = i;
}
}
return min_idx;
}
// 다익스트라
void Dijkstra()
{
for (int i = 1; i <= N; i++)
dist[i] = map[start][i]; // 시작 노드와 인접한 정점에 대해 거리 계산
dist[start] = 0;
visited[start] = true;
for (int i = 0; i < N - 1; i++)
{
int new_node = FindSmallestNode();
visited[new_node] = true;
for(int j = 0; j <= N; j++)
{
if (visited[j] == true)
continue;
if (dist[j] > dist[new_node] + map[new_node][j])
dist[j] = dist[new_node] + map[new_node][j];
}
}
}파이썬으로 구현한 코드는 아래 링크를 참고한다.
💎 [Python] 최단경로를 위한 다익스트라(Dijkstra) 알고리즘
3. 구현(2): 우선순위 큐
3-1. 특징
순차 탐색을 사용할 경우 노드 개수에 따라 탐색 시간이 매우 오래 걸릴 수 있다. 이를 개선하기 위해 우선순위 큐를 도입하기도 한다.
거리 값을 담을 우선순위 큐는 힙으로 구현하고, 만약 최소 힙으로 구현한다면 매번 루트 노드가 최소 거리를 가지는 노드가 될 것이다.
파이썬의 경우 PriorityQueue나 heapq 라이브러리로 우선순위 큐, 최소 힙이 지원되며, C++의 경우 <queue> 라이브러리에서 최대 힙을 지원하는 priority_queue 를 사용할 수 있다. 최대 힙을 최소 힙으로 쓰려면 저장되는 값에 -를 붙여 음수로 만들면 된다.
우선순위 큐에서 사용할 '우선순위'의 기준은 '시작 노드로부터 가장 가까운 노드'가 된다. 따라서 큐의 정렬은 최단 거리인 노드를 기준으로 최단 거리를 가지는 노드를 앞에 배치한다.
위의 순차 탐색을 쓰는 구현과는 다르게 우선순위 큐를 사용하면 방문 여부를 기록할 배열은 없어도 된다. 우선순위 큐가 알아서 최단 거리의 노드를 앞으로 정렬하므로 기존 최단 거리보다 크다면 무시하면 그만이다. 만약 기존 최단거리보다 더 작은 값을 가지는 노드가 있다면 그 노드와 거리를 우선순위 큐에 넣는다. 우선순위 큐에 삽입되는 형태는 <거리, 노드> 꼴이다.
3-2. 동작 예시
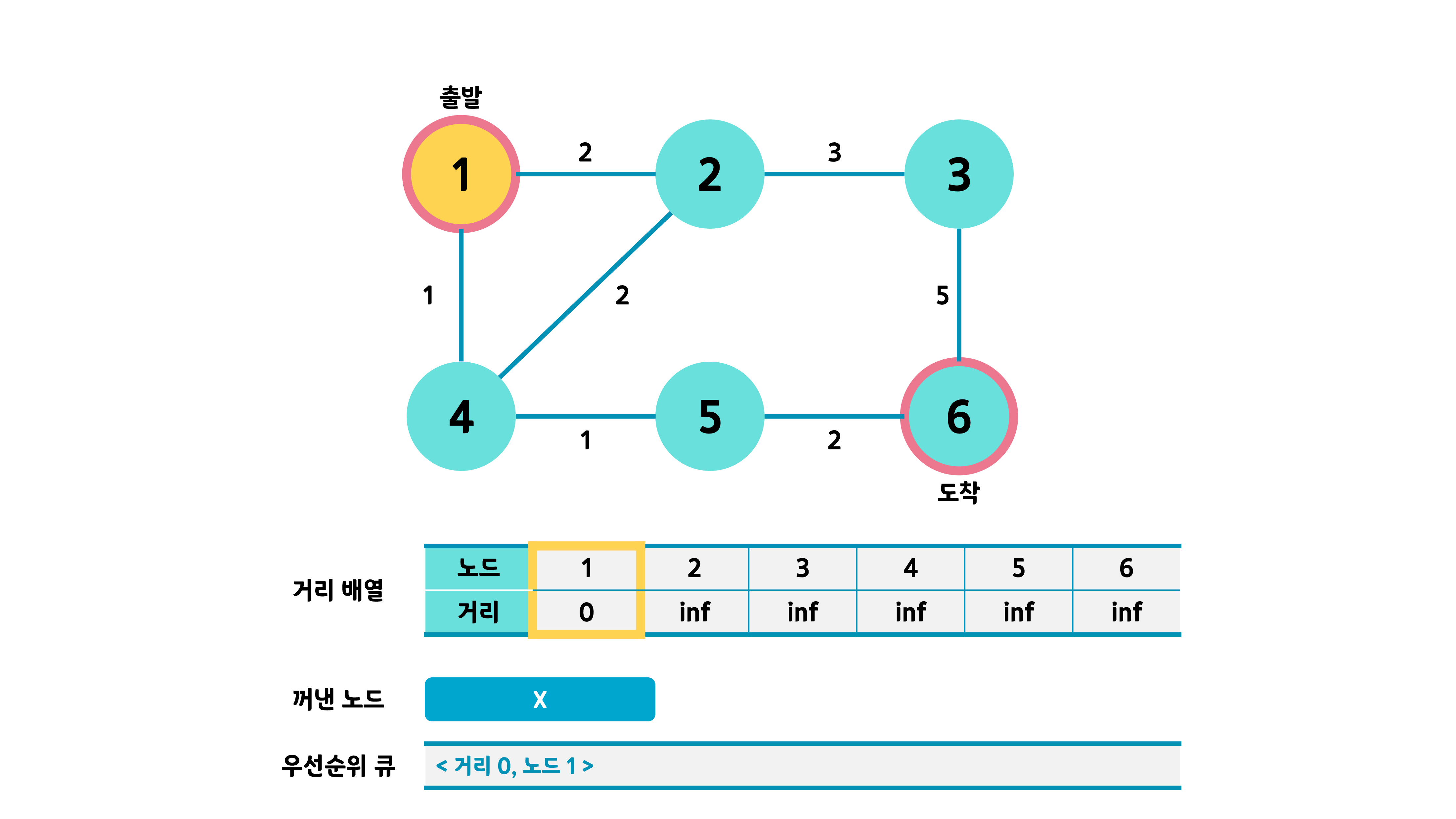
출발 노드인 1번의 거리를 업데이트하고 우선순위 큐에 넣는다.
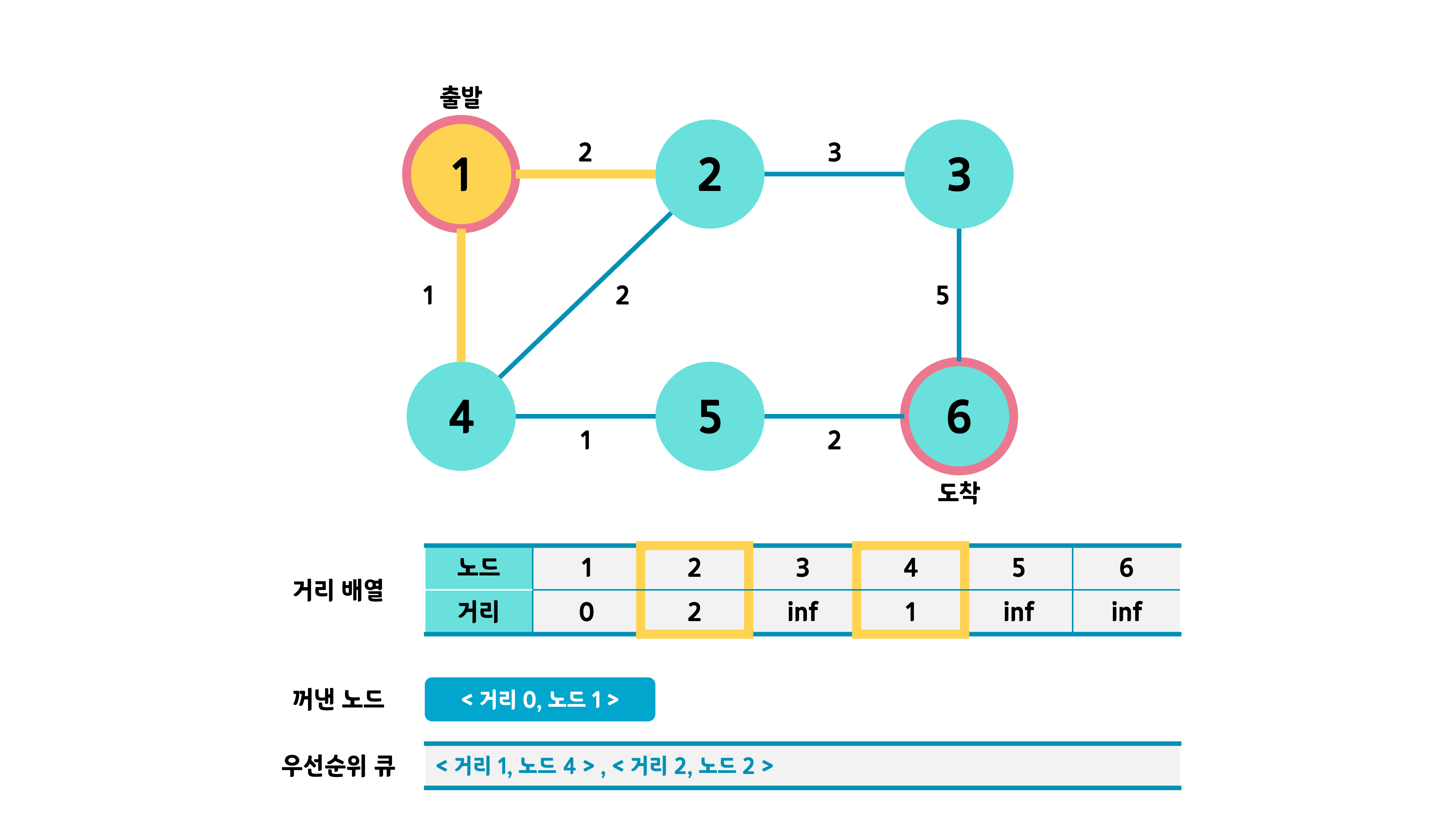
큐에서 맨 앞 노드인 <거리 0, 노드 1>을 꺼내 그 인접 노드를 조사한다. 거리값이 업데이트 되는 노드만, 즉 최소 거리로 업데이트 되는 노드만 큐에 넣는다. 큐는 거리값이 작은 순서대로 정렬된다.
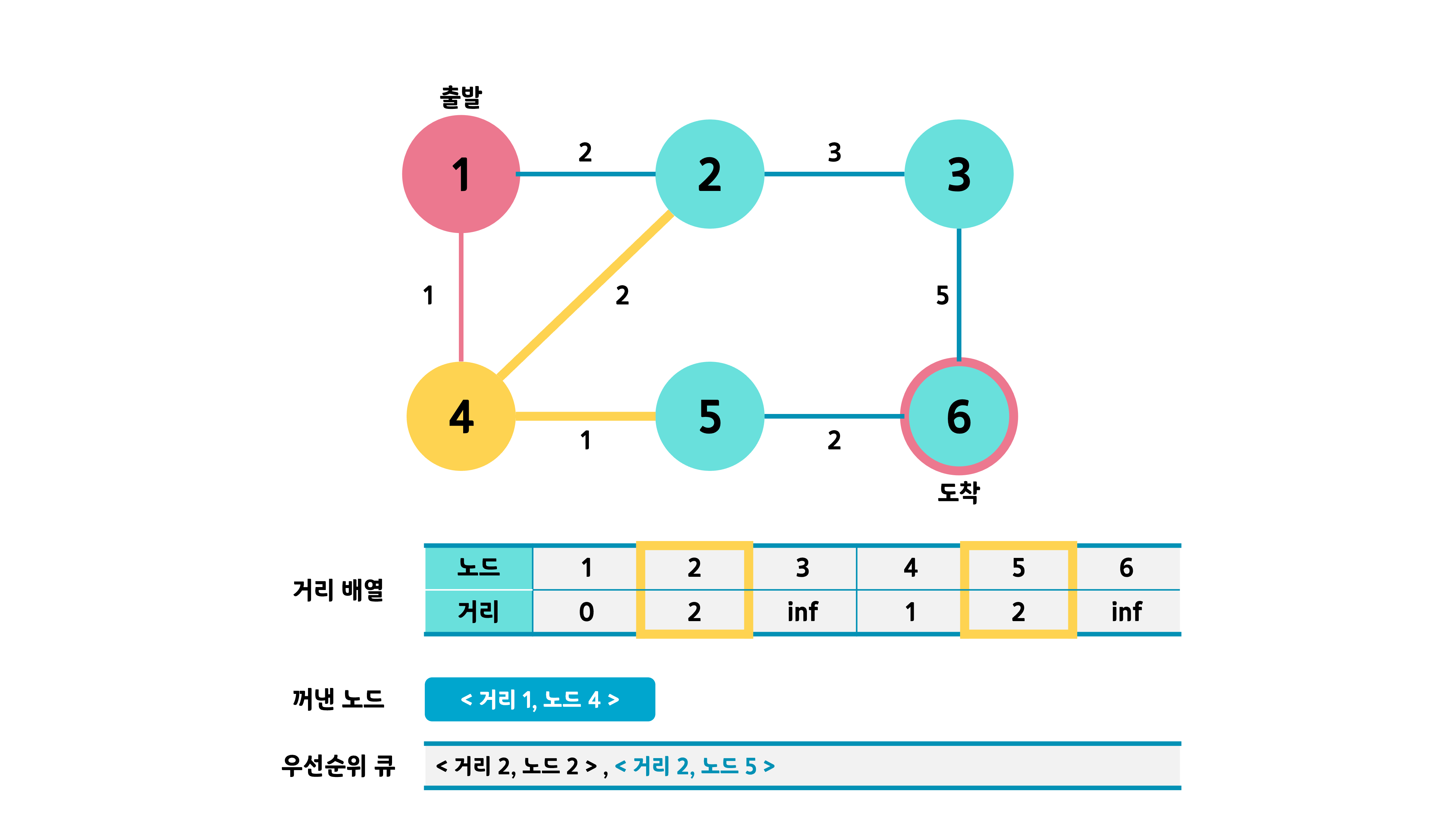
<거리 1, 노드 4>를 꺼내 그 인접 노드를 조사한다. 최소 거리로 거리가 업데이트 된 5번을 큐에 넣는다. 2번의 경우 기존의 거리값인 2보다 1 + 2 = 3이 더 크므로 2번은 큐에 넣지 않는다.
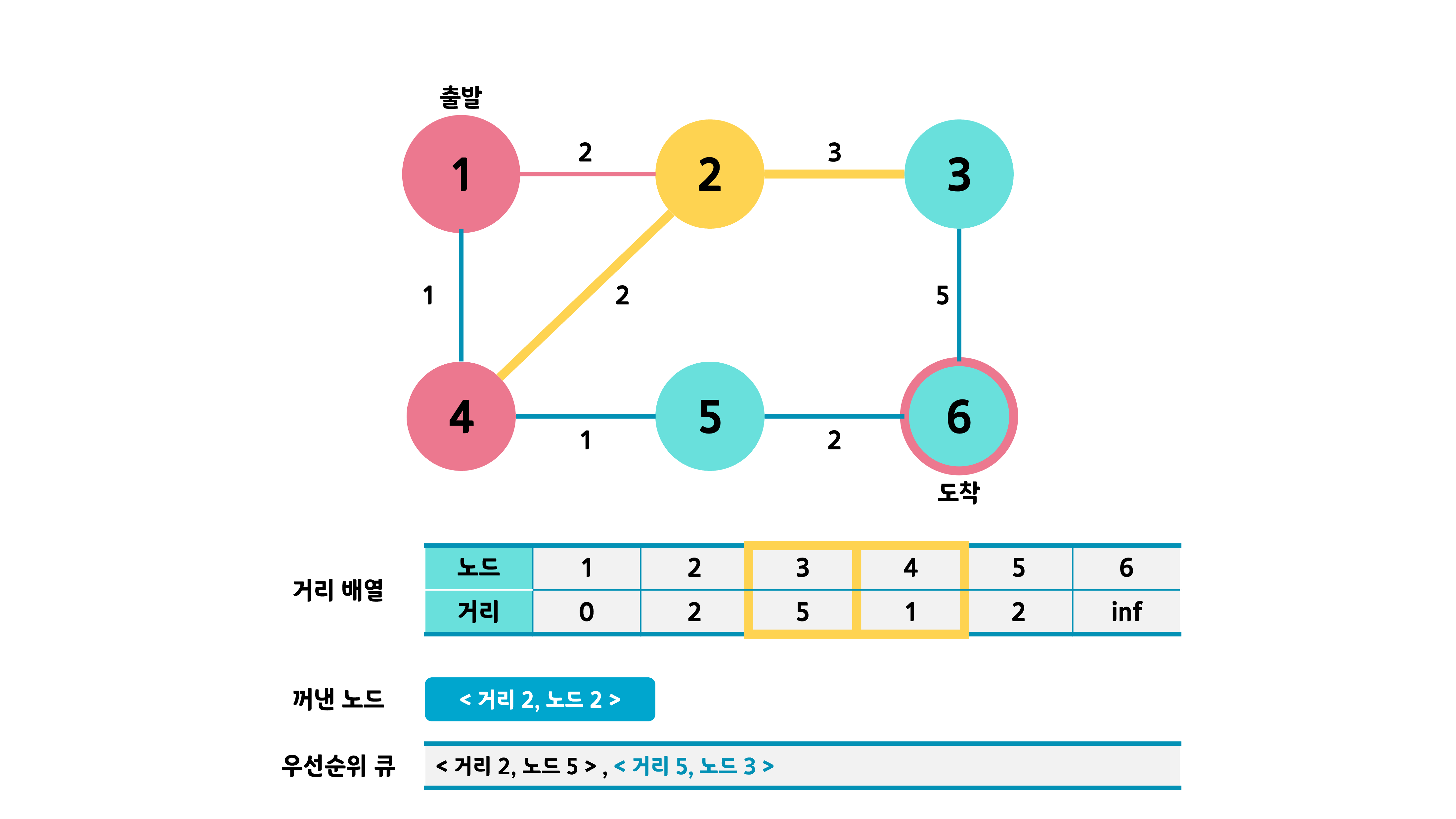
같은 과정의 반복으로 <거리 2, 노드 2>의 인접 노드를 조사하고 거리값이 갱신된 노드만 큐에 넣는다. 3번이 큐에 들어간다.
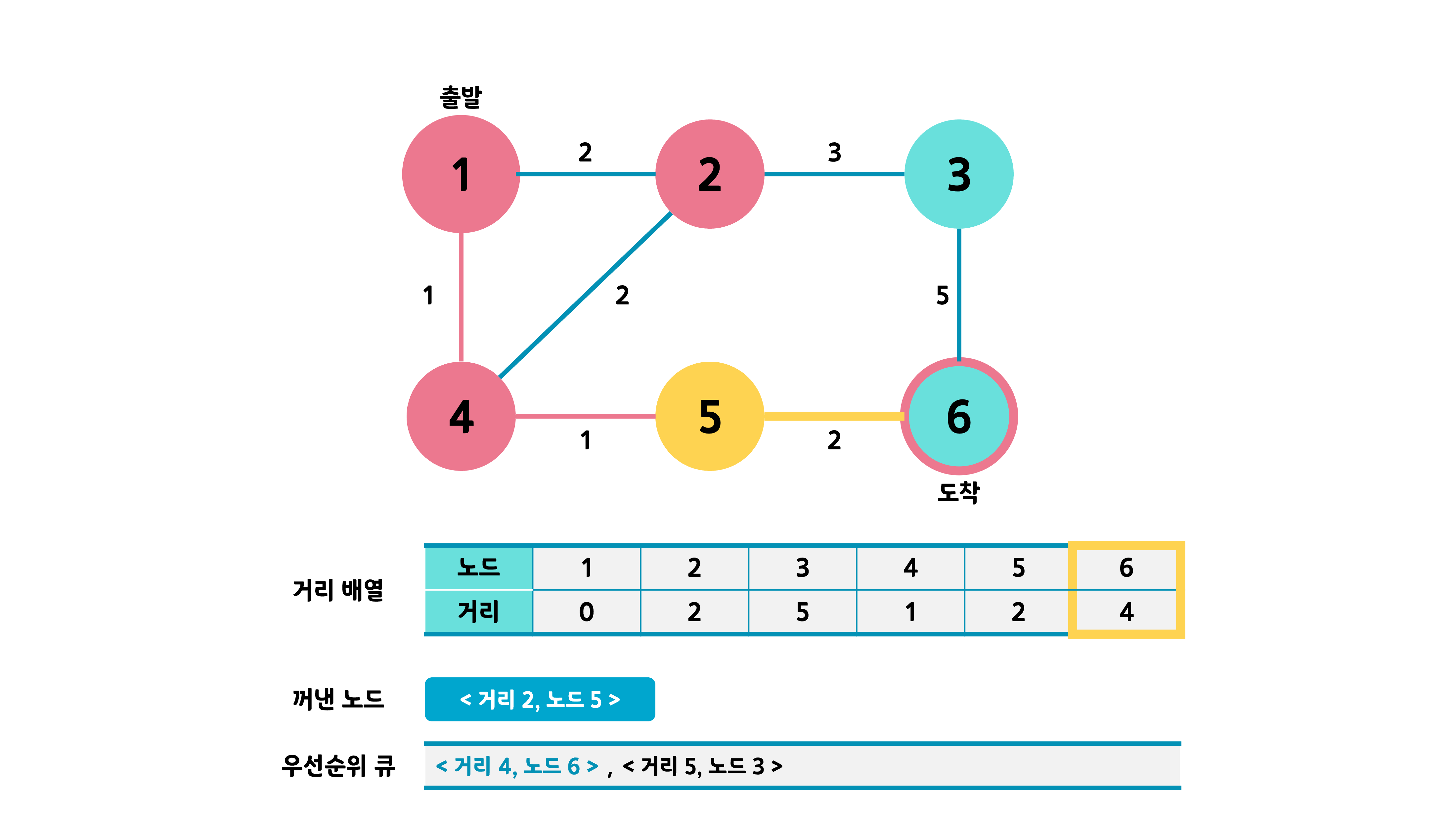
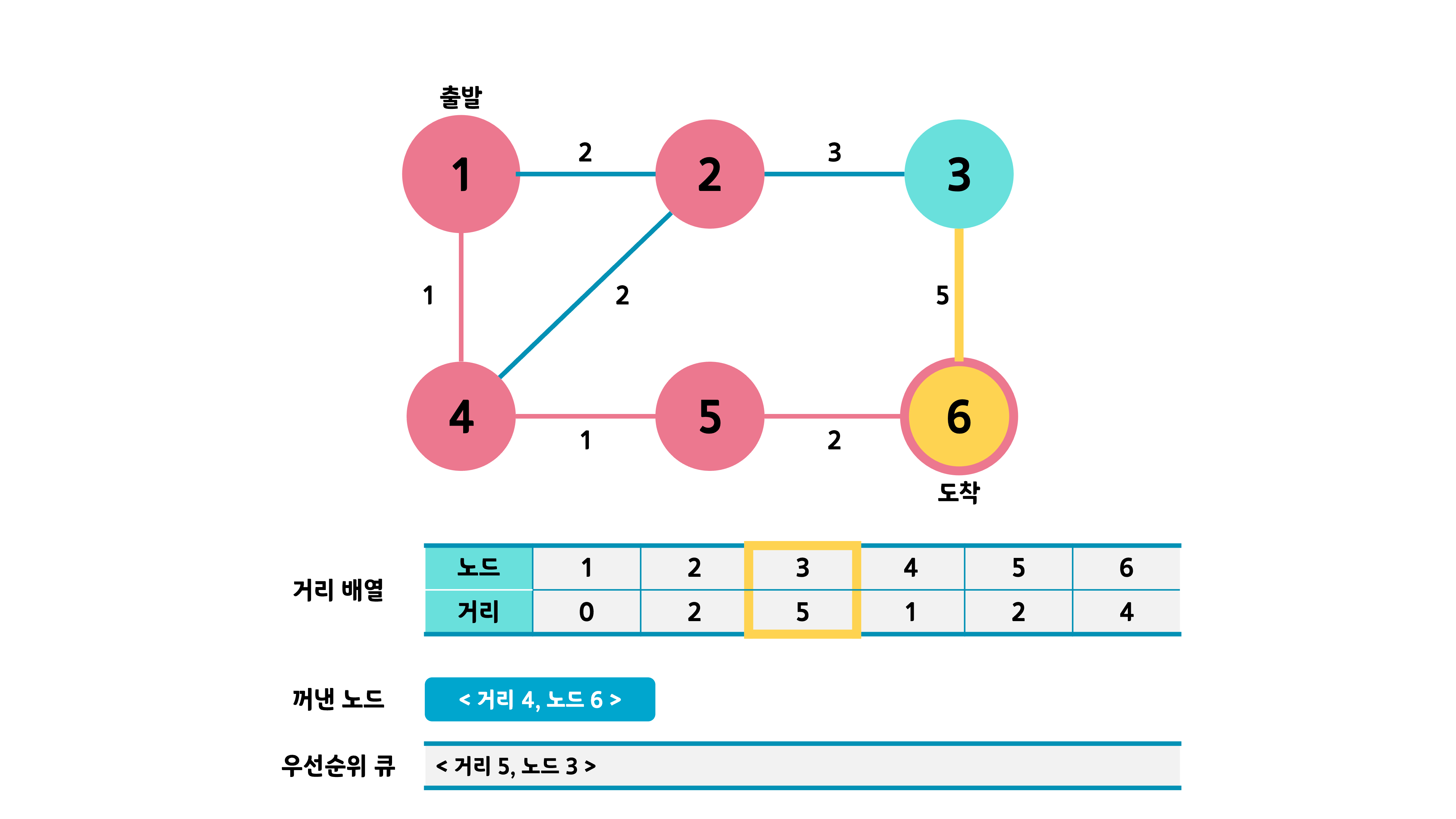
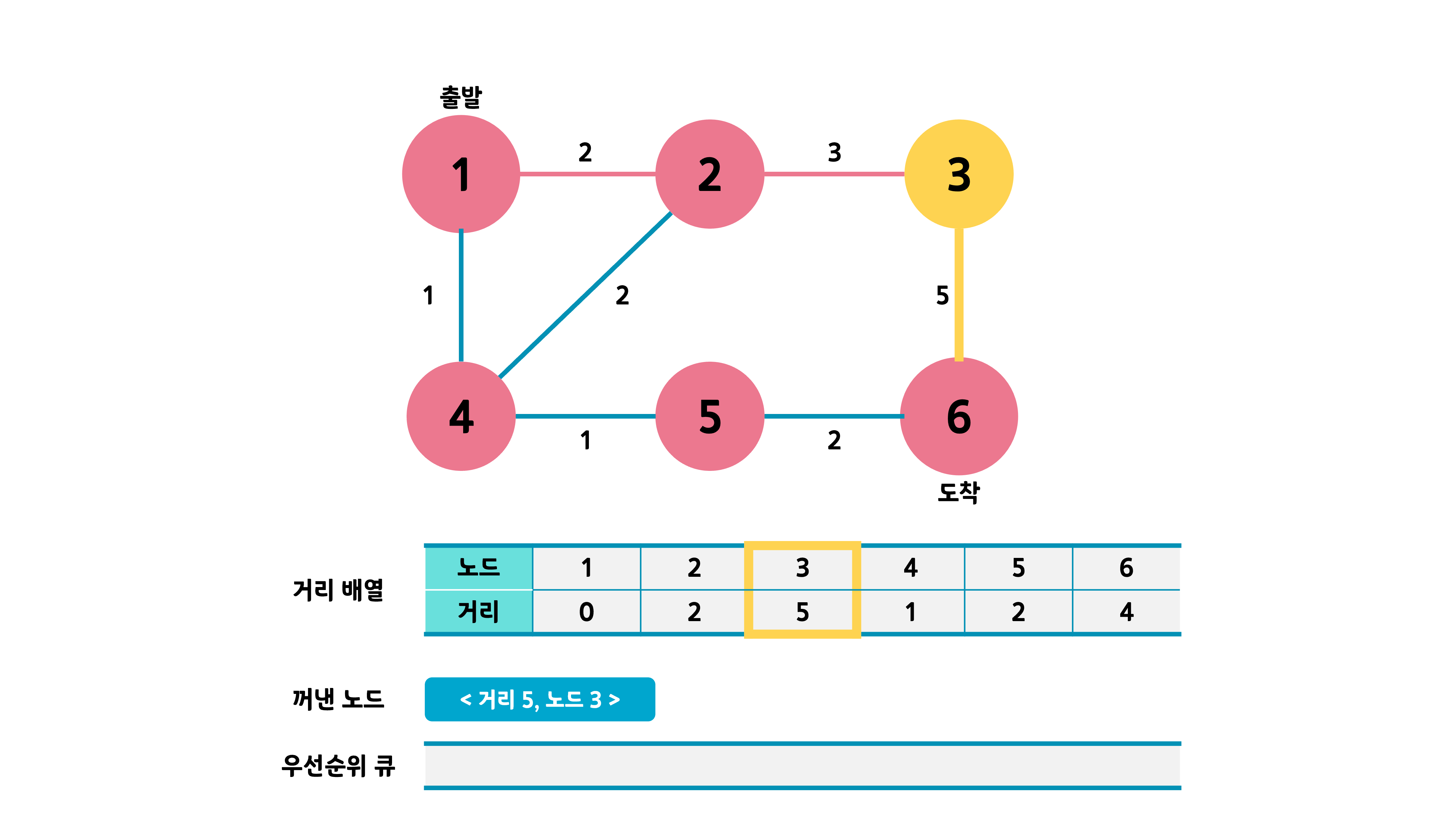
큐가 빌 때까지 해당 과정을 반복한다.
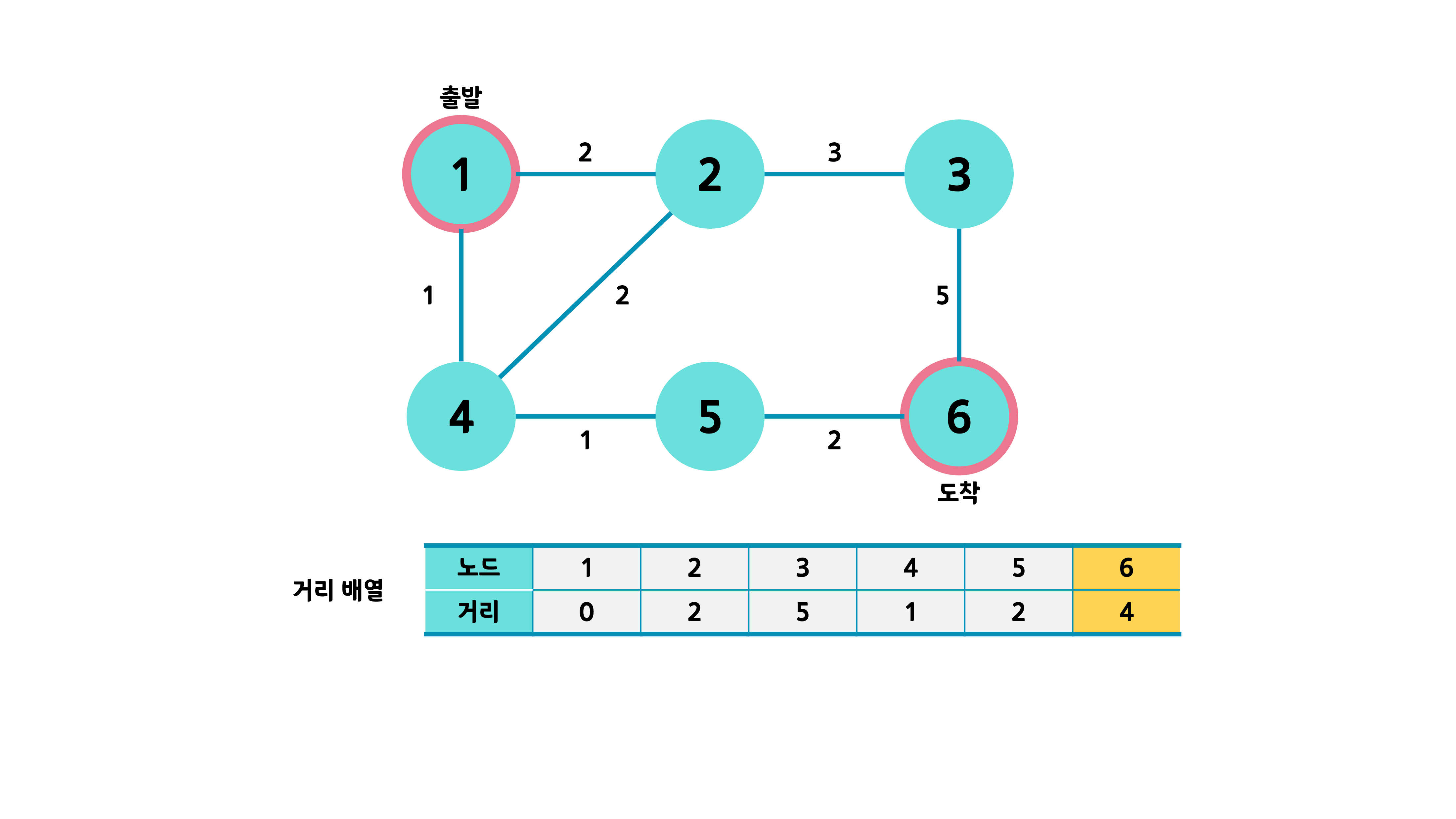
최종적으로 도착 노드의 거리 값이 최소 거리가 된다.
3-3. 코드 구현
그래프의 형태는 '시작 노드 / 끝 노드 / 그 사이 간선의 가중치'를 입력 받아 인접 행렬 graph[][]에 넣어 표현한다.
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
# define INF 99999999
// 시작 위치와 정점의 개수, 인접 행렬을 받아
// 최소 거리 행렬을 반환함
vector<int> dijkstra(int start, int N, vector<pair<int, int>> graph[])
{
vector<int> dist(N, INF); // 거리를 저장할 리스트 초기화
priority_queue<pair<int, int>> pq; // 우선순위 큐 선언
dist[start] = 0; // 시작 노드 거리를 0으로 함
pq.push({ 0, start }); // 우선순위 큐에 넣기
while (!pq.empty())
{
int cur_dist = -pq.top().first; // 큐에서 꺼내 방문하고 있는 정점의 거리
int cur_node = pq.top().second; // 정점의 인덱스(번호)
pq.pop();
for (int i = 0; i < graph[cur_node].size(); i++)
{
int nxt_node = graph[cur_node][i].first; // 인접 정점 번호
int nxt_dist = cur_dist + graph[cur_node][i].second; // 인접 정점까지 거리
if (nxt_dist < dist[nxt_node]) // 지금 계산한 것이 기존 거리값보다 작다면
{
dist[nxt_node] = nxt_dist; // 거리값 업데이트
pq.push({ -nxt_dist, nxt_node }); // 우선순위 큐에 넣기
}
}
}
return dist; // start 노드로부터 각 노드까지 최단거리를 담은 벡터 리턴
}
int main()
{
const int N = 10; // 노드의 개수가 10개라 가정.
int E = 20; // 간선의 개수가 20개라 가정.
vector<pair<int, int>> graph[N]; // 그래프 형태 선언
for (int i = 0; i < E; i++)
{
int from, to, cost; // 간선의 시작점, 끝점, 가중치
cin >> from >> to >> cost;
graph[from].push_back({ to, cost }); // 무향 그래프라 가정하므로 시작점과 끝점 둘 다 벡터에 넣어야 함
graph[to].push_back({ from, cost });
}
vector<int> dist = dijkstra(0, N, graph);
cout << "끝점까지의 최단거리" << dist[N - 1] << endl;
return 0;
}파이썬으로 구현한 코드는 아래 링크를 참고한다.
💎 Python으로 다익스트라(dijkstra) 알고리즘 구현하기
💎 [Python] 우선순위 큐를 활용한 개선된 다익스트라(Dijkstra) 알고리즘
3-4. 시간 복잡도
간선의 수를 E(Edge), 노드의 수를 V(Vertex)라고 했을 때 가 된다.
우선순위 큐에서 꺼낸 노드는 연결된 노드만 탐색하므로 최악의 경우라도 총 간선 수인 E만큼만 반복한다. 즉 하나의 간선에 대해서는 이고, E는 보다 항상 작기 때문에 E개의 간선을 우선순위 큐에 넣었다 빼는 최악의 경우에 대해서는 이다.
참고 자료
- YounghunJo, "
[Python] 최단경로를 위한 다익스트라(Dijkstra) 알고리즘," Tistory - 앎의 공간 - 해피니s, "[알고리즘] 다익스트라(Dijkstra) 알고리즘이란? | c++ 다익스트라 구현," Tistory - code_lab
- Min Jae Park, "Python으로 다익스트라(dijkstra) 알고리즘 구현하기," justkode
- YounghunJo, "[Python] 우선순위 큐를 활용한 개선된 다익스트라(Dijkstra) 알고리즘," Tistory - 앏의 공간
- 얍문, "[ 다익스트라 알고리즘 ] 개념과 구현방법 (C++)," Tistory - 얍문's Coding World
- 공부하는 식빵맘, "Chapter 4-5. 다익스트라 최단 경로 알고리즘," GitHub blog - 평생 공부 블로그 : Today I Learned
8개의 댓글
죄송합니다. 저도 헷갈려서 다시쓰네요. https://www.acmicpc.net/problem/1916 이 경우에는 방문처리를 남겨야하던데.. 음 잘모르겠네요








덕분에 좋은 내용 잘 보고 갑니다
감사합니다.