Eigenvalue & Eigenvector

sy_healing·2022년 4월 13일

Eigenvalue Eigenvector dimensionality reduction vector transformation

선형대수

목록 보기

2/4

✍️ Vector transformation

2차원 공간에서의 벡터변환, 즉 선형 변환은 임의의 두 벡터를 더하거나 혹은 스칼라 값을 곱하는 것을 의미한다.

임의의 두 벡터 더해서 방향 바꾸기: $T(u+v) = T(u)+T(v)$
스칼라 값을 곱해서 크기 바꾸기: $T(cu)=cT(u)$

한 점을 한 벡터 공간에서 다른 벡터 공간으로 이동시키는 이동 규칙을 정의하는 함수이다.
transformation은 matrix를 곱하는 것을 통해 벡터(데이터)를 다른 위치로 옮긴다라는 의미를 가지고 있다.

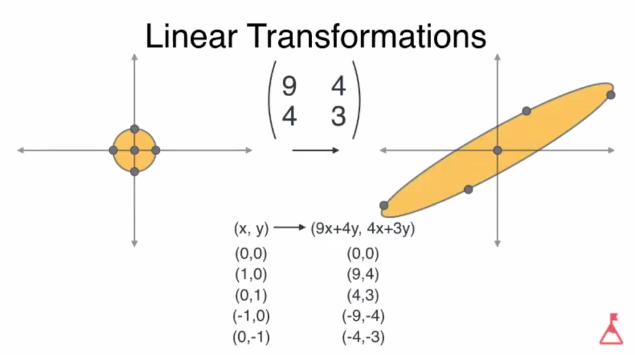
Matrix와 Vector의 곱으로 표현

2차원 평면 상의 모든 벡터는 기저벡터의 선형결합으로 표현된다. 임의의 벡터에 대한 변환이 이루어지면 이 벡터를 구성하는 기저벡터도 함께 변화하고, 이를 통해 기저벡터가 어떻게 바뀌는지 추적이 가능하다.

예로 아래는 임의의 벡터 a에 매트릭스 T를 곱하여 벡터 b로 변환한 것이다.

f(\begin{bmatrix}x_1\\x_2\\ \end{bmatrix}) = \begin{bmatrix}2x_1+x_2\\x_1-3x_2\\ \end{bmatrix} = b

a=\begin{bmatrix}x_1\\x_2\\ \end{bmatrix},\; T=\begin{bmatrix}2&1\\1&-3\\ \end{bmatrix}

벡터를 변환하는 이유는 뭘까?

벡터 변환을 하는 이유는 다양한 feature를 가진 데이터들의 차원을 감소시키기 위해서다.
정사영(projection) 역시 벡터를 다른 벡터와 같은 방향으로 변환시키는 것이니 일종의 벡터 변환이라고 볼 수 있다.

✍️Eigenvector(고유벡터) & Eigenvalue(고유값)

고유벡터란 변환에 의해 영향을 받지 않는 벡터이다. (단, 영 벡터는 제외한다.)
즉, 임의의 벡터를 변환시키기 위해 특정 매트릭스 T를 곱했을 때, 그 결과과 벡터의 방향이 바뀌지 않고 스칼라배 한 값이 나온다면 그 벡터는 T의 고유벡터가 된다.

고유 벡터는 매트릭스를 곱했을 때 길이만 변화하게 되는데 그 길이의 변화 스칼라 값을 고유값(λ)이라고 한다.

$T⋅v=v ′ =λ⋅v$

\begin{bmatrix} 4&2 \\ 2&4 \\ \end{bmatrix} \begin{bmatrix} 3 \\ -3 \\ \end{bmatrix} = \begin{bmatrix} 6 \\ -6 \\ \end{bmatrix} = 2\begin{bmatrix} 3 \\ -3 \\ \end{bmatrix}

위의 식에서 보자면 다음과 같이 나타낼 수 있다.

eigenvector = \begin{bmatrix} 3 \\ -3 \\ \end{bmatrix},\;eigenvalue = 2

Python에서 numpy를 통해 고유값과 고유벡터의 값을 도출해 낼 수 있다.

import numpy as np

eigen_val, eigen_vec = np.linalg.eig(matrix)

✍️ Dimensionality Reduction(차원축소)

고차원의 문제는 Feature 수가 많은 데이터셋을 모델링 혹은 분석 할 때 생기는 여러 문제점들이다.
이러한 문제는 Dimensionality Reduction 통해 해결 할 수 있는데, 왜 차원의 수를 감소시키는 걸까?

차원 감소의 이유

메모리 공간을 절약
크게 의미를 가지지 않는 feature의 제거
고차원의 데이터는 시각화 분석이 어려움
feature가 샘플의 수에 비해 많으면 머신러닝의 Overfitting(과적합) 우려가 발생.

즉, Dimensionality Reduction은 빅데이터에 대한 적절한 처리를 통해 충분한 의미를 유지하면서 더 작은 부분을 선택하는 기술이다.

Feature Extraction & Feature Selection

Feature Extraction
여러 feature들을 조합해서 더 적은 수의 feature로 변환하는 것이다.
feature 간의 연관성을 고려해 새로운 feature를 생성하는 장점이 있지만, 해석이 다소 어렵다는 단점도 있다.

Feature Selection
여러 feature들 중에서 중요하다고 생각되는 feature는 남기고 나머지는 제거하는 방법이다.

✍️ Orthogonality(직교)

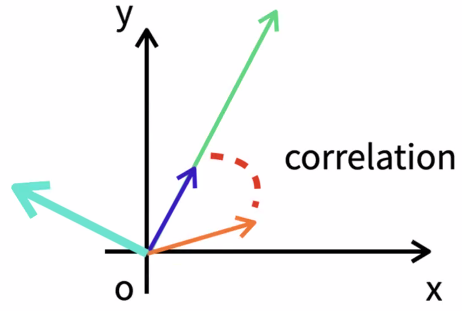
직교란? 벡터와 매트릭스가 서로 수직인 상태를 말한다. 수직이란 것은 서로 전혀 상관관계가 없이 독립적인 상태라는 것이다. 아래 그림에서 파란색 벡터와 왼쪽의 하늘색 벡터는 서로 직교하며, 하나의 벡터가 변화할 때 다른 벡터에 전혀 영향을 주지 않는다.

벡터의 직교를 확인하는 방법 : 벡터의 내적이 0

✍️ 단위 벡터(Unit Vector)

단위 벡터란 길이가 1인 벡터이다.

단위벡터는 벡터의 크기로 나누어서 구할 수 있으며, 이를 벡터의 정규화 라고 한다.
예를 들어 [3, 4]의 벡터의 크기는 $\sqrt(3^2+4^2)=5$ 이다. 즉, 이 벡터의 단위벡터는 (0.6, 0.8)이 된다.

생각해보면 모든 벡터와 매트릭스는 단위벡터의 선형조합으로 표현할 수 있다.
(2, 5, 10)인 벡터의 경우 위 그림의 3차원 단위벡터로 표현하자면 2hat(i) + 5hat(j) + 10hat(k) 이다.

sy_healing

이전 포스트

Vector & Matrix

다음 포스트