데이터 사이언스와 선형대수의 관계?

잘 정리된 사이트
위 블로그 글을 읽고 조금은 '아! 그렇구나' 라고 받아들였으나, 내가 정리하기엔 어려움이 있다.
가끔 왜 하는건지 이해하지 못하고 답답할 때, 왜 필요한지에 대해 해당 블로그를 통해서 상기시켜야겠다.

해당 블로그에서 말하는 결론
• 데이터를 벡터로 쉽게 표현 가능
• 벡터가 모인 행렬로 인해 데이터 표현 식을 찾는데 용이함

---

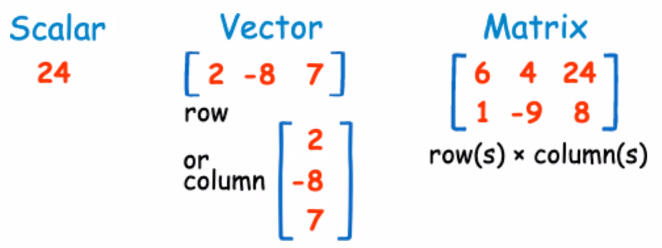
선형대수에서 다루는 데이터는 갯수나 형태에 따라 scalar, vector, matrix, tensor로 나뉜다.

💡 데이터의 유형

• 스칼라 : 하나의 숫자로만 이루어진 데이터 (크기만 있고 방향이 없는 물리량)
• 벡터 : 여러 숫자로 이루어진 데이터 레코드. 크기(정도)와 방향을 가지고 있으며, 사물의 움직임을 프로그래밍하기 위한 가장 기본적인 구성 요소
• 매트릭스 : 벡터가 여럿인 데이터집합
• 텐서 : 같은 크기의 행렬이 여러개 있는 것

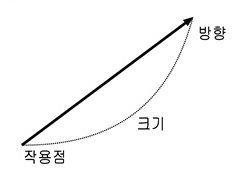
벡터는 화살표를 통해 표현하게 되는데, 화살표의 길이로 벡터의 크기(Norm)을 표현하고, 화살표의 방향을 통해 벡터의 방향을 나타낸다.

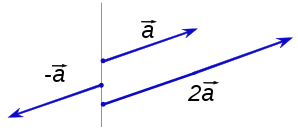
벡터의 크기는 스칼라배를 통해 표현할 수 있다.
스칼라배란 벡터의 크기만큼 곱하는 것인데, 방향은 유지한 채 벡터의 길이만 수치만큼 늘어난다.

✍️ 벡터의 내적(Dot Product)

*내적이란 어떤 두 개의 벡터 쌍이 있고 그 쌍으로 부터 만들어지는 스칼라 값이다.
이 스칼라 값을 추가로 사용해 생성된 벡터 공간을 내적 공간이라고 한다.

같은 위치의 컴포넌트끼리 계산이 되므로, 내적을 위한 두 벡터의 차원은 동일해야 한다.
또한 교환 법칙과 분배 법칙이 적용된다.

내적은 어디에 사용되는 걸까?

1. 직교성 판별
   : 내적은 두 벡터가 직교인지 아닌데 판단하는데 사용한다.
   두 벡터의 내적 값이 0이면 두 벡터는 직교한다고 본다.

2. cos 값 측정
   : 실제 cosθ 의 값을 몰라도 곱셈, 덧셈으로 이를 구할 수 있다. 이는 그래픽에서 많이 사용된다고 한다.

3. 방향 판별
   : 물체의 앞, 뒤를 빠르게 파악할 수 있다. 게임 로직에서 시야 혹은 방향 판별에 많이 사용된다.

4. 투영 벡터
   : 내적을 통해 하나의 벡터를 다른 벡터에 투영한 벡터를 구할 수 있다.

   📖 Python 예제

   # array a, b
   import numpy as np
   np.dot(a,b)       #내적
   
   np.matmul(a,b)
   
   '''
   numpy의 dot 과 matmul 은 2차원 행렬의 곱셈에서는 같은 기능을 수행한다고 한다.
   하지만 고차원 배열 또는 텐서의 곱셈에서는 용법이 전혀 다름을 알아두자!
   '''
   

   💡 매트릭스(Matrix)

   벡터는 여러 개의 스칼라 값의 모음이었다면, 매트릭스는 여러 개의 벡터 모음이라고 생각하면 쉽다.
   벡터에도 차원이 있듯, 매트릭스에도 차원이 있는데 (행, 열) 순으로 표기한다.
   아래 그림의 경우 X 매트릭스의 차원은 (3, 3)차원, Y는 (2, 3)차원이다.

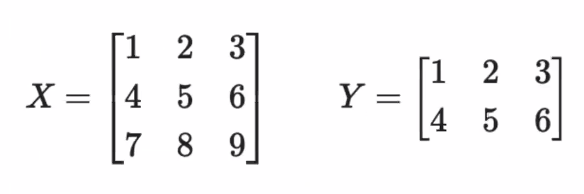
✍️ 전치(T)

• 전치란 행과 열을 바꾸는 것이다. 주어진 매트릭스에서 (1, 1), (2, 2) … 값에 대각선을 긋고, 그 선을 기준으로 뒤집으면 된다.

아래 매트릭스에서는 (1, 1)인 1과 (2, 2)인 4를 기준으로 대각선을 긋고 뒤집으면 확인 가능하다.

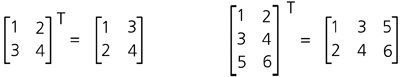
✍️ 정사각 매트릭스(square matrix)

• 행과 열의 수가 동일한 매트릭스이다. (정사각 형태를 띄는 매트릭스)

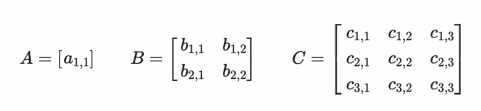
✍️ 대각 매트릭스(Diagonal matrix)

• 대각선에만 값이 존재하고, 나머지는 전부 0인 매트릭스

✍️ 상삼각 & 하삼각(Upper & Lower Triangular)

• 대각선 위/아래만 값이 있고, 나머지는 전부 0인 매트릭스

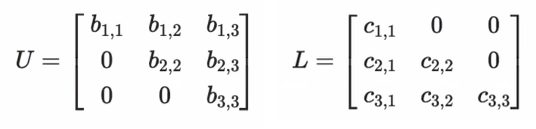
✍️ 단위 매트릭스(Identity matrix)

• 대각선 원소는 1, 나머지는 모두 0인 매트릭스

단위 행렬 해석

1. A * I == A
즉, 정방 행렬에 단위 행렬을 곱하면 원본 정방 행렬이 출력됨.
2. A * A-1(역행렬) == I
임의의 매트릭스에 역행렬을 곱했을 경우 단위 행렬이 출력됨.

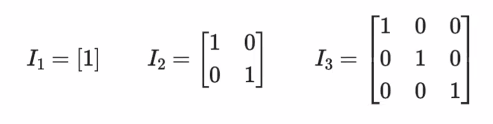
✍️행렬식 (Determinant)

• 모든 정사각 매트릭스가 갖는 속성으로 행렬을 하나의 스칼라 값으로 표현하는 방법인데, 데이터의 속성을 숫자 하나로 압축해서 표현하는 것이다.
• 행렬식은 역행렬의 존재 유무, 선형변환의 해석에 이용된다.
  (행렬식 = 0 인 경우 역행렬이 존재하지 않음)

표기 : det(A), |A|

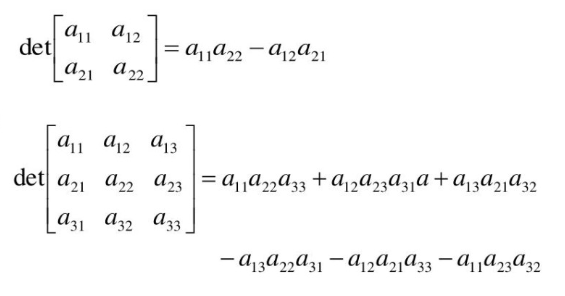
📖 Python 예제

x = np.array()
determinant = np.linalg.det(x)

✍️ 역행렬(Inverse Matrix)

• 임의의 행렬을 곱했을 때 결과가 단위 행렬이 나오는 행렬
• 역행렬은 선형방정식 풀이에 이용된다.
  (행렬에는 나눗셈이 정의되지 않는데, 나눗셈을 대신해 역행렬을 곱하고 방정식의 해를 도출함)

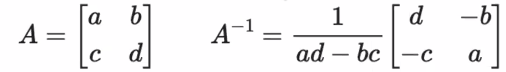
역행렬을 구할 수 없는 경우
1. 행렬식이 0 인 경우 (=특이 매트릭스)
2. 정방 행렬이 아닌 경우
3. 데이터의 구조가 행렬의 형태가 아닌 경우. (1차원 X)

📖 Python 예제

 x = np.array()
inv_mat = np.linalg.inv(x)

# 매트릭스의 차원 확인
x.ndim