경사하강법에 대한 이야기를 하기 전에 '미분'에 대한 내용이 필요하다.
고등학교 때 하던 수학을 10년이 더 지나서 마주하자니 당혹스럽지만, 왜 데이터사이언스에 필요한지 생각해 볼 필요가 있다.
💡 데이터 사이언스에 왜 미분이 필요한가?
들어가기 전에 미분, 편미분, chain rule의 기본 개념을 알고 가자.
✍️ 미분
- 미분이란 어떤 함수로부터 그 함수 기울기를 출력하는 새로운 함수를 만들어내는 것이다.
미분으로 만들어진 함수는 도함수라고 한다.
알아두면 좋은 기본 미분공식
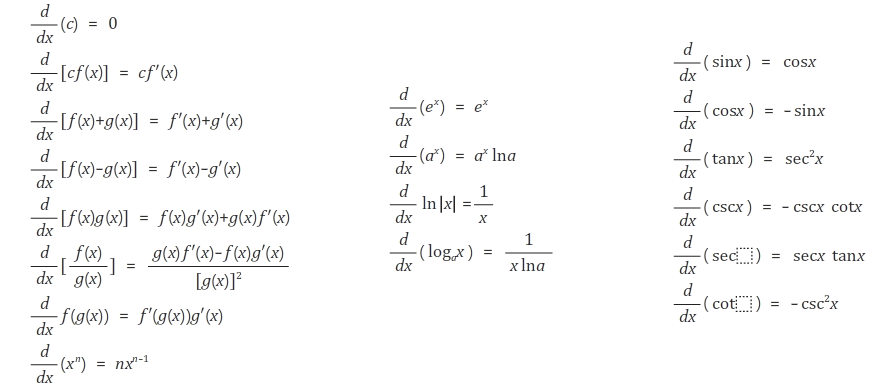
✍️ 편미분
- 편미분이란 함수가 둘 이상의 독립변수를 가지는 다변수 함수일 때에도 미분을 통해 기울기는 하나의 변수에 대해서만 구할 수 있다는 것이다.
결국 편미분으로 인해 하나의 함수에서 여러개의 도함수가 나올 수 있다.
위의 함수를 x에 대해 미분할 경우, y에 대해 미분할 경우 다음과 같은 값이 나온다.
✍️ Chain Rule
- 함수의 함수를 미분하는 방식이다. 즉, 합성함수의 미분을 생각하면 된다.
chain rule은 딥러닝의 핵심 개념 중 하나인 Backward Propagation에 필요하기 때문에 중요하다.
기본 공식은 다음과 같다.
예를 들어 생각해보자.
🔍 미분이 필요한 이유
우리는 이미 발생한 현상에 대한 단순 해석을 넘어, 미래를 예측하기 위한 머신러닝, 딥러닝 등 다양한 기술을 활용한다. 이때 중요한 것은 더욱 정확한 예측을 하는 것이다.
- 이러한 예측을 위해 만들어 놓은 틀이 모델이고, 이 모델의 예측도를 높여 나가는 일련의 작업을 최적화라고 한다. (파라미터를 조정하며 진행)
- 미분은 이 '최적화' 작업에 있어서 필요적인 요소이다.
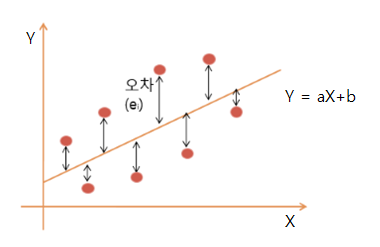
아래의 그림을 보면, 점들은 전체 데이터를 직선 Y=aX+b 는 예측 모델이라고 할 수 있다.
하지만 데이터 점들이 모델과 정확히 일치하지 않고, 오차(error)가 발생한다. 이 오차의 값들을 나타낸 것이 바로 손실함수이다.
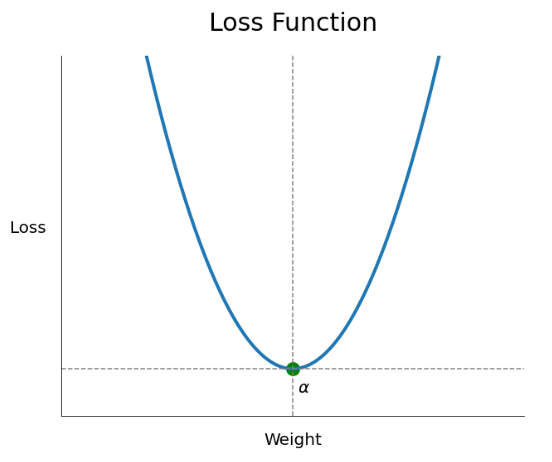
대락적으로 error 값들을 정리해서 손실 함수를 나타내면 아래와 같은 형태를 띈다.
그럼 우리는 error가 최소화 되는 지점, 즉 해당 그래프에서 가장 오목한 부분을 찾을 것이다.
그 순간의 a, b 값이 바로 최적의 파라미터가 되는 것이다.
결론은 더 정확한 예측을 하는 것이 우리의 목표인데, 이때 오차함수의 기울기가 0이 되는 지점 즉, 미분했을 때 0이 나오는 지점으로 가야 더 정확한 예측이 가능해진다. 그래서 미분이 필요하다는 것이다!
💡경사하강법 (Gradient Descent)
- 경사하강법은 위에서 말한 손실 함수 값을 최소화하는 a, b를 찾을 수 있는 최적화 알고리즘의 대표적인 예시이다.
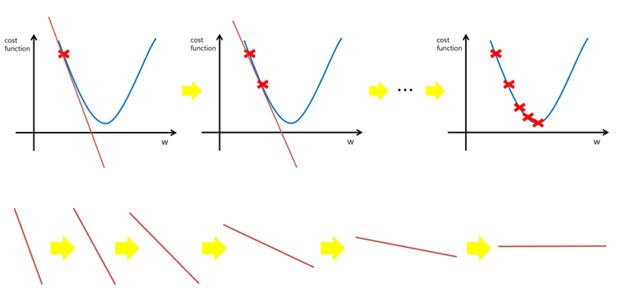
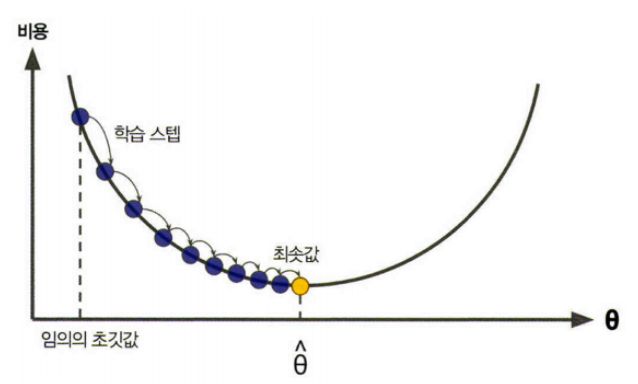
아래 그림을 보면 이해가 쉬워진다.
우리는 목표는 손실함수에서 기울기가 0 (미분값이 0)인 지점을 찾는 것이다.
먼저 임의의 a, b 값을 정하고(그림에서 빨간색 x) 점점 기울기를 낮춰가면서 기울기가 0이 지점이 나올 때 까지 반복한다. 이 과정을 경사하강법이라고 한다.
이때 중요한 것이 학습률(learning rate)이다.
학습률은 우리가 직접 설정해주어야 하는 값인 하이퍼 파라미터(hyper parameter)인데, 학습률에 따라 이동하는 수준이 달라지기 때문에 잘 설정할 필요가 있다.
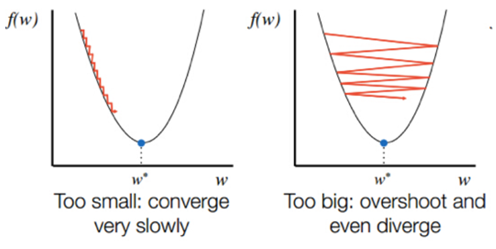
만약 학습률을 너무 작게 설정할 경우 학습률이 높다 할 지라도 움직이는 거리가 줄어든다. 결국 큰 고랑에 빠지게 되면 나오지 못하고 수렴할 수도 있게 된다. 또한, 반복하는 데이터의 양도 많아지고 학습 시간도 늘어나게 된다. (아래 사진의 왼쪽)
반면에 지나치게 학습률이 높은 경우에는 학습 시간은 적게 걸리나, 스텝이 너무 커서 전역 최솟값(global minimum)이 있는 영역을 건너 뛰어 지역 최솟값에서 수렴 할 수도 있다. (아래 사진의 오른쪽)
참고로, 전역(global)과 지역(local)이 존재하는 것은 우리가 다루는 것이 고차원이기 때문이다.