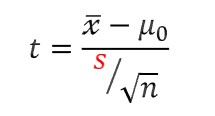💡 가설(Hypothesis)

가설이란 '아마도 그럴 것이다.'라는 잠정적인 주장이다. 예를 들어, '지구는 둥글 것이다.'와 같은.
그러나 통계에서 사용하는 가설은 조금 다른다. 통계적 가설은 모집단의 모수(ex: 평균, 분산 등)에 대한 잠정적인 주장이다. 통계적 가설에서는 귀무가설과 대립가설을 설정해주어야 한다.

✍️ 귀무가설(Null hypothesis : H0)

• '아무런 차이가 없다', '전혀 효과가 없다' 는 것을 주장하는 것으로, 영가설이라고도 한다.
  연구에서는 귀무가설을 거부하기 위해 설정한다.

✍️ 대립가설(Alternative hypothesis : H1)

• 귀무가설이 기각될 경우 채택하는 가설로, '차이가 있다', '효과가 있다' 라고 주장하는 것이다.
  연구에서는 연구자가 증명하고 싶은 가설을 말한다.

---

💡 가설 검정

• 모집단에 대한 주장과 관련해, 표본의 정보를 사용해서 가설이 맞는지 아닌지 판정하는 과정이다.

✍️ 단측 & 양측 검정 (One/Two tailed test)

단측 검정은 data A의 평균이 data B의 평균보다 큰지 작은지를 검정하고,
양측 검정은 data A와 data B 평균의 차이가 있는지 없는지(즉, 같은지 다른지)를 검정한다.

다시 말해

* one-tailed test

H0 : A = B
H1 : A < B or A > B

* two-tailed test

H0 : A = B
H1 : A != B

📖 Python

from scipy import stats

stats.ttest_ind(data A, data B, alternative='greater/less')

# alternative = 대립가설을 설정해준다고 보면 됨.
# greater 로 설정 시 대립가설 : data A > data B
# less 로 설정 시 대립가설 : data B > data A

[내가 이해하기 위한 메모]
가설 검정을 할 때는 모집단의 표준편차를 아는 경우와 모르는 경우로 나눠 생각해보면 쉽다.
모표준편차을 알 경우, 확률분포로 정규분포를 사용한다.
모표준편차를 모를 경우, t-분포를 사용하는데, 만약 표본의 수(n) >= 30 일 경우는 t-분포는 값이 정규분포와 비슷해지기 때문에 정규분포를 사용한다.

✍️ 검정통계량

• 검정통계량이란 수집한 데이터를 이용해 계산한 '확률 변수'이다.

쉽게 생각하면 이렇다. 우리는 표본 집단으로부터 표본평균, 표본편차 등 표본 통계량을 얻게된다. 이 표본통계량이 가설검정에서는 검정통계량이라고 불린다.
가설 검정을 할 때는 확률 분포를 활용하는데, 연구에 적용하는 통계기법이 사용하는 함수에 따라 다른 검정 통계량을 사용한다.

확률변수	검정통계량
z-검정: 정규분포	Z-통계량
t-검정: T-분포	t-value
카이제곰검정: 카이제곱분포	x^2-value
ANOVA검정(분산분석): F-분포	F-value

주의할 점은 검정통계량을 통해서 확률을 구하는게 아니라는 거다.
검정 통계량은 그래프 x축의 좌표를 구하는 것이다.

검정통계량 공식 을 봐도 알 수 있다. 이는 좌표값을 구하는 식이다.