✍️ 분산(Variance, var) & 표준편차(Standard deviation, std)
- 분산 : 하나의 확률 변수가 흩어진 정도를 측정하는 측도이다.
(데이터가 얼마나 퍼져있는지 측정하는 방법) - 표준편차 : 분산에 루트를 씌운 값
* 일반적으로 분산이라 함은 표본분산 계산식을 사용한다. 모집단의 분산을 구하기엔 n이 너무 많기 때문.
이 표본분산이 n이 아닌 n-1로 나누는 이유는 값의 정확도가 더 높기 때문이라고 한다.
(자세한 증명은 눈으로만 익혔다;)
* 분산을 구하는 과정에서 제곱 값을 더했다. 이런 경우 음수값을 제거(?)하는 효과는 있지만,
스케일이 커지는 문제가 발생하는데, 표준편차는 이를 해결하기 위해 스케일을 낮춘 방법이다.
그래서 많은 통계 분석 프로세스에서 표준편차를 사용해서 계산한다.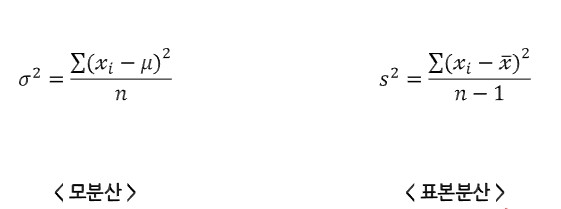
📖 Python
#분산
import pandas as pd
import numpy as np
rand_var = random.sample(range(0, 100), 50)
rand_var.var( ddof=0 ) # ddof = 자유도, default = 0
#표준편차
rand_var.std( ddof=0 )💡공분산(Covariance)
- 공분산은 두 개의 확률변수가 흩어진 정도를 측정하는 측도이다.
(두 개의 데이터가 얼마나 퍼져 있는지를 측정하는 방법)
즉, 하나의 변수 값이 변할 때, 다른 변수가 어떤 연관성을 나타내며 변화하는지 측정하는 것.
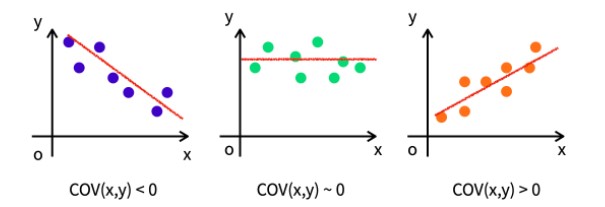
아래 그림을 보자.
첫번째 : x와 y의 값이 반비례 관계(음의 상관관계)를 가진다. ->공분산 음수
두번째 : x와 y의 관련성을 알알 수가 없는 경우 0에 가까운 공분산이 출력된다. 두 변수가 서로 독립적이라면 공분산이 0이 되는데, 공분산이 0이라고 해서 항상 독립적인 것은 아니기때문에 주의할 필요가 있다.
세번째 : x와 y의 값이 비례(양의 상관관계)를 가진다. ->공분산 양수
공분산의 값이 크다는 것은 두 변수 간 연관성이 크다는 의미이다.
그러나 스케일로 인해 실제 변수의 연관성과 상관없이 큰 공분산 값을 가지게 되는 경우도 발생하므로 주의해야한다.
📖 Python
import numpy as np
v1 = np.array([1, 2, 3, 4])
v2 = np.array([5, 6, 7, 8])
cov = np.cov( v1, v2 )
# 공분산의 행렬이 출력된다. 공분산 값은 아래와 같이 출력되므로
# 만약 공분산만! 출력하고 싶다면 뒤에 [0, 1] 혹은 [1, 0]을 붙이면 된다.
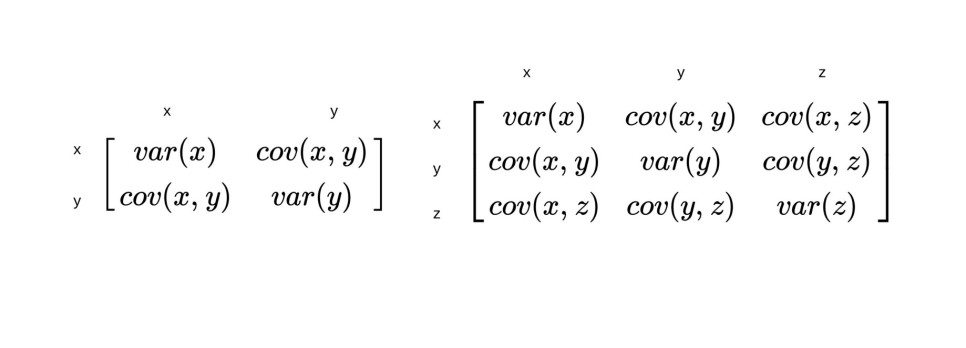
💡상관계수(Covariance)
- 상관계수는 공분산을 두 변수의 표준편차로 각각 나누어 준 값이다.
공분산 역시 분산을 구하는 것이라 스케일이 커지는데, 이 스케일을 조정하기 위해서이다.
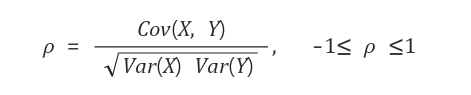
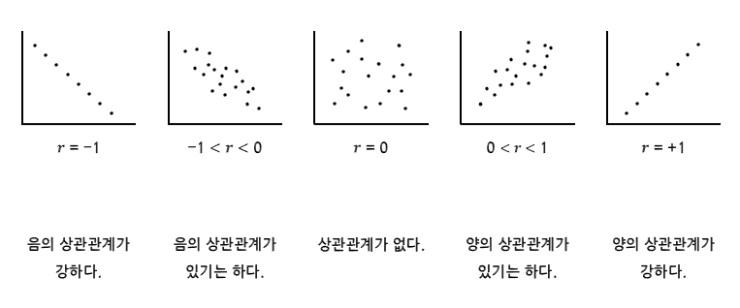
상관계수는 두 변수의 상관관계 를 타나낸다.
그럼 공분산과 무엇이 다른가?
공분산은 값에 범위가 없다. 따라서 여러 값을 비교하고자 할 때 기준이 없으니 어려움이 있다.
반면 상관 계수는 1에서 -1 사이의 정해진 범위 안에서 값을 가지기 때문에 비교에 용이하다.
따라서 스케일이나 단위의 영향을 받지 않고, 데이터의 평균이나 분산의 크기에도 영향을 받지 않는다.
피어슨 & 스피어만 상관계수
피어슨 : 모수적 상관계수
스피어만 : 비모수적 상관계수
📖 Python
import numpy as np
v1 = np.array([1, 2, 3, 4])
v2 = np.array([5, 6, 7, 8])
corr = np.corrcoef(v1, v2)
# 뒤에 [0, 1] 혹은 [1, 0]