베이지안 정리

sy_healing·2022년 4월 22일

통계

목록 보기

9/10

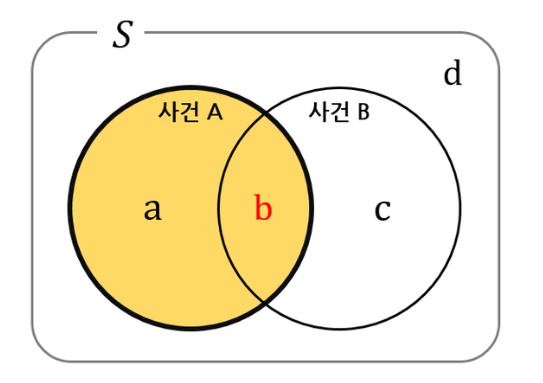
조건부 확률이란 어떤 사건(A)이 일어난 가정 하에 사건(B)가 일어날 확률인 P(B|A) 이다.

P(B|A) = \frac{P(B \cap A)}{P(A)}

위 그림에서는 P(B|A) = b / a+b 가 된다.

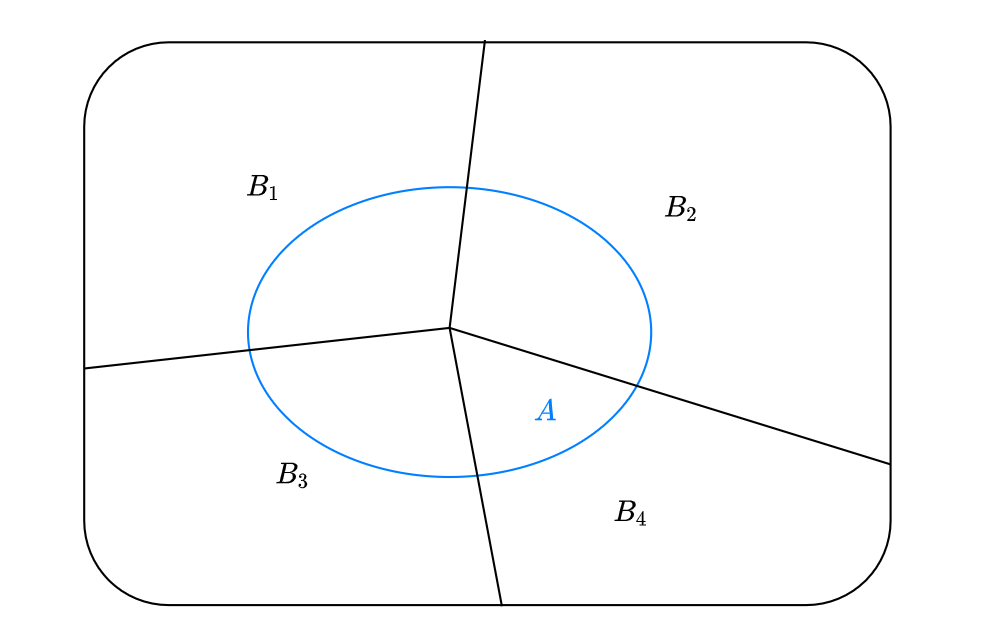
전확률의 법칙은 A의 모든 확률은, 주어진 Bn(B1, B2, B3, ...) 에 대해서 각각의 일어날 확률의 총 합 이다는 것이다.

P(A) = P(A∩B1) + P(A∩B2) + P(A∩B3) + P(A∩B4)

P(A)= P(A|B1)*P(B1) + P(A|B2)*P(B2) + ... + P(A|Bn)*P(Bn)

결국

P(A) = \displaystyle\sum_{n}^{\infin}{P(A|B_n)P(B_n)}

이해를 위해 예시를 들어보자. 넷플릭스를 통해 영화를 봤다고 하자면,

A : 영화를 본 경우
B : 코믹 영화를 본 경우(B1) / 코믹 영화가 아닌 경우(B2)

코믹의 유무를 떠나 영화를 본 확률을 구하고자 한다면 이런 개념이다.

P(영화 봄) = P(영화|코믹영화 봄)•P(코믹영화 봄) + P(영화봄|코믹영화 아님)•P(코믹영화 아님)

베이즈 정리란 위의 조건부 확률과 전확률 법칙을 적용해서 만든 일종의 공식이다.

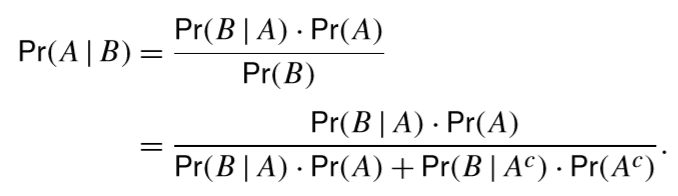
공식을 자세히 살펴보면 첫 번째 줄에서 조건부 확률을, 두 번째 줄에서 전확률의 법칙을 이용해 식을 변환시켰음을 볼 수 있다.

'사전 확률을 통해서 사후 확률을 얻어 지속적으로 업데이트를 한다'는 것이다.
당연한 것이겠지만 데이터가 많을 수록 올바른 결정을 내릴 확률이 높아진다.
(베이즈 정리는 앞으로 배울 머신러닝에 굉장히 많이 사용된다.)

다시 예를 들어 생각해보자.
영화를 본 사람이 마음에 든 영화에는 좋아요를 눌렀다.

 P(A) : 영화를 보고 좋아요를 누른 확률 (사전확률)
 P(B) : 시청한 영화가 코믹 영화인 확률
 P(B|A) : 좋아요를 누른 영화 중 코믹 영화인 확률
 P(B|Ac) : 좋아요를 누르지 않은 영화 중 코믹 영화인 확률

$P(A)$ = 50%, $P(B|A)$ = 60%, $P(B|Ac)$ = 20% 라고 가정한다.

코믹 영화를 봤을 때 좋아요를 누를 확률 $P(A|B)$ 를 구해보자!

 0.6 * 0.5 / (0.6)*(0.5) + (0.2)*(0.5) 로 75% 의 확률이 나온다.

이렇게 도출된 $P(A|B)$ 는 사후 확률이라고 한다.

넷플릭스는 이 알고리즘을 통해 코믹 영화를 추천했을 때 시청자가 75%의 확률로 좋아할 것이라는 사실을 업데이트하게된다. 이후 시청자가 지속적으로 넷플릭스를 이용한다면 그에 따라 알고리즘이 업데이트 되고 시청자에게 더 적합한 영화를 추천해준다.