파이썬으로 구현하는 저주파 필터(Low Pass Filter, LPF)

1. 필터

제어공학에서 말하는 "필터"는 간단하게 생각하면 입력받은 데이터를 적절히 걸러서 원하는 값을 얻는 것입니다. 대표적인 필터들로 연속적인 입력값들의 평균을 반환하는 평균 필터나, 노이즈를 제거하는 것에 자주 사용하는 저주파 필터등이 있습니다.
이번 글에서는 그 중에서 노이즈 제거에 사용하는 저주파 필터에 대하여 간단하게 설명하고, 파이썬으로 직접 구현해보도록 하겠습니다.

2. 저주파 필터

저주파 필터의 목적은 노이즈 제거입니다. 정확하게 말하면, 저주파 필터의 정의는 고주파는 거르고, 저주파는 통과시키는 필터인데, 일반적으로 센서 데이터에서 노이즈는 고주파에 해당되고, 우리가 원하는 센서의 데이터는 저주파에 해당되기 때문에, 저주파 필터를 이용하면 노이즈를 필터링 할 수 있게 되는 것입니다.

그렇다면 저주파 필터의 원리는 무엇일까요? 이 글에서는 저주파 필터를 파이썬으로 구현하는 방법에 대하여 다루지만, 원래는 물리적인 RC 회로로 구현되는 것이 저주파 필터입니다.

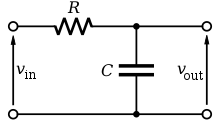
위 사진은 가장 고전적 저주파 필터인 1차 RC 회로입니다. v_in으로 센서 데이터 등 입력값이 전압의 형태로 들어가면, RC회로를 거쳐서 v_out으로 나오는 데이터는 필터링 된 데이터가 나오는 형태인데, 이를 소프트웨어 적으로 구현하는 것입니다.

3. 미분 방정식

그렇다면 어떻게 위의 회로를 소프트웨어로, 파이썬으로 옮길 수 있을까요? 그 답은 바로 수학입니다.

3문단에서 다룰 내용은 "그냥 이런 이론을 통하여 파이썬으로 옮긴다"를 설명하기 위한 내용이기 때문에, 이 내용에 관심이 없다면 4문단으로 가도 무방하니 참고 바랍니다.

또한, 이 내용을 이해하기 위하여 필요한 지식은 다음과 같습니다.

• 키르히호프의 전압법칙
• 라플라스 변환
• 전달 함수

위에 존재하는 1차 RC 회로의 미분 방정식을 키르히호프의 전압법칙에서 유도하면 아래와 같습니다

(v_o은 v_out, v_i는 v_in)

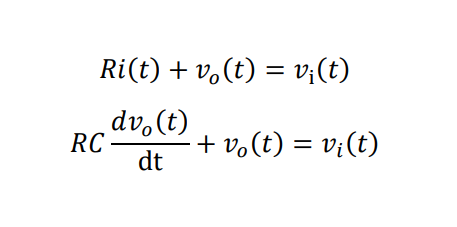
이를 공대생의 영원한 친구 라플라스 변환을 통하여 s-domain으로 옮기면 아래와 같이 나타나게 됩니다.

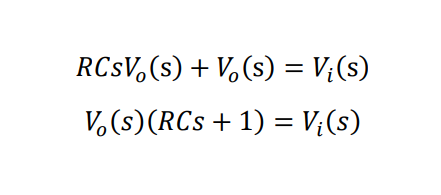
(도함수의 라플라스 변환은 L{f'(t)}=sL{f(t)}-f(0)입니다)

이를 V_i과 V_o의 전달함수 형태로 표현하면 아래와 같습니다.

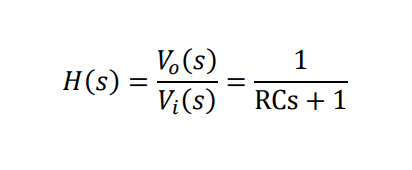
이때 RC를 시상수(τ)로 표현하면 아래와 같이 표현할 수 있습니다.

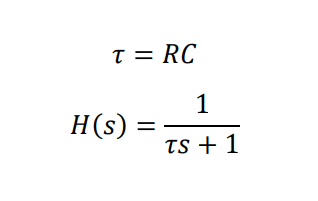
그렇다면 위 시스템은 아래와 같은 형태로 표현할 수 있습니다.

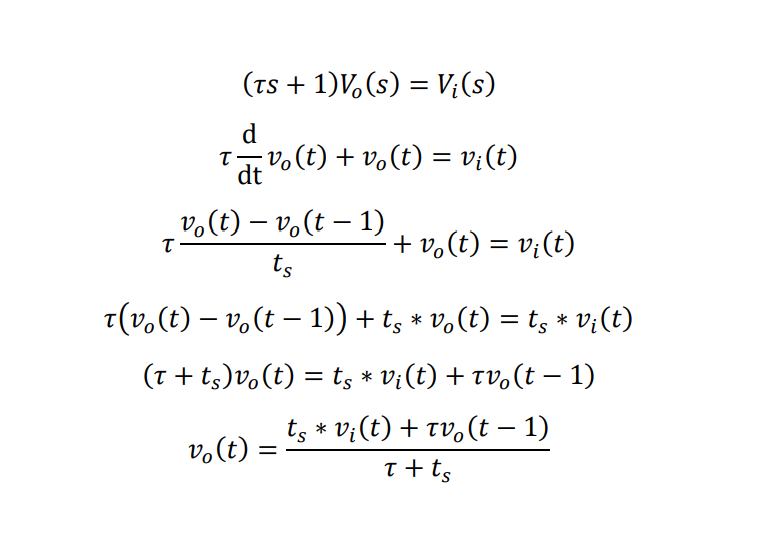
전달함수를 역라플라스 변환 한 뒤에, v_o의 도함수를 풀어쓰고, 다시 v_o에 대하여 정리한 것입니다. 여기서 t_s는 데이터와 데이터 사이의 시간간격(데이터 주기의 역수)이고, 타우는 시상수입니다. 또한, v_o(t-1)은 전 데이터의 값입니다.

보다시피, 일종의 재귀 함수의 형태로 RC 회로의 미분 방정식을 풀어낸 것을 확인할 수 있습니다.

4. 파이썬으로 구현

최종적인 식

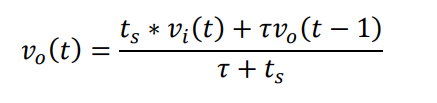
을 파이썬으로 구현하면 아래와 같이 표현할 수 있습니다.

import numpy as np

class LowPassFilter(object):
    def __init__(self, cut_off_freqency, ts):
    	# cut_off_freqency: 차단 주파수
        # ts: 주기
        
        self.ts = ts
        self.cut_off_freqency = cut_off_freqency
        self.tau = self.get_tau()

        self.prev_data = 0.
        
    def get_tau(self):
        return 1 / (2 * np.pi * self.cut_off_freqency)

    def filter(self, data):
        val = (self.ts * data + self.tau * self.prev_data) / (self.tau + self.ts)
        self.prev_data = val
        return val

저주파 필터 클래스로 표현하였고, 실제 사용한 예제는 아래와 같습니다.

class PID(object):
	def __init__(self):
    	self.lpf = LowPassFilter(1., 1/10)
		rospy.Subscriber("load", Float32, self.load_callback)

    def load_callback(self, msg):
        data = self.lpf(msg.data)
        self.load = data

(제가 작업에 필요해서 사용한 코드입니다. ROS와 기타 센서 퍼블리셔가 필요하기 때문에, 위 코드로 똑같이 확인 하는 것은 불가능합니다)

그리고 위의 코드를 실제로 실행시켰을 때, 나온 결과 값입니다.

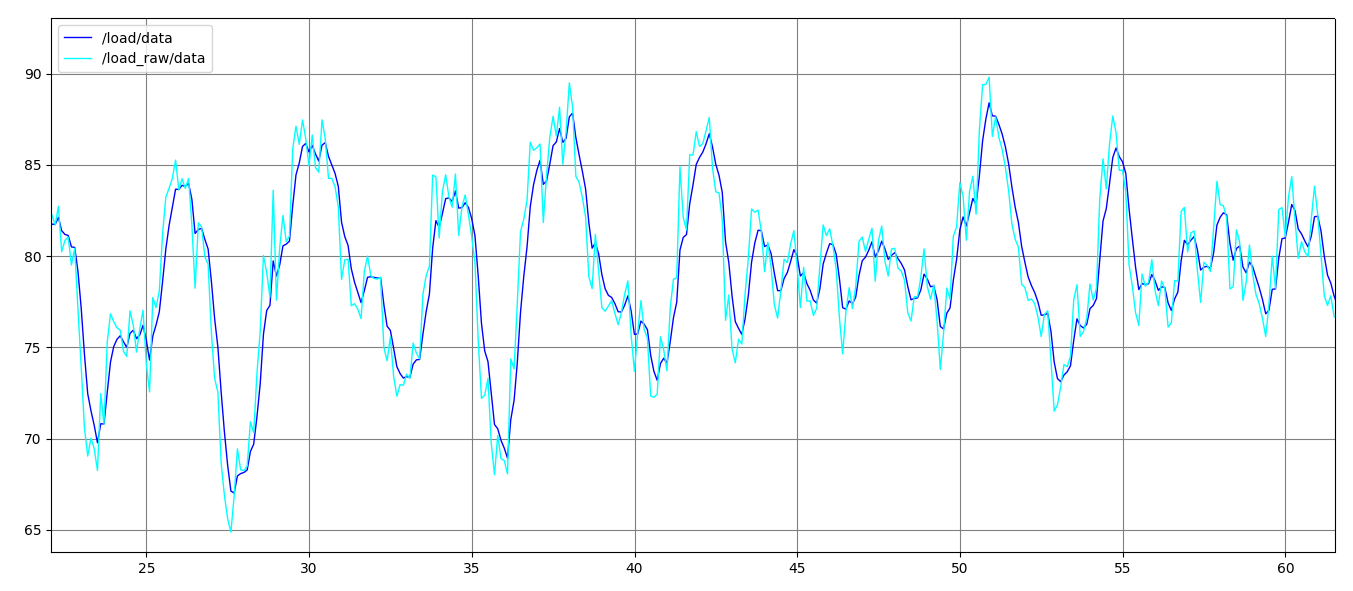
하늘색으로 표현된 데이터가 저주파 필터가 적용되기 전, 적용되기 후입니다. 의도한 결과대로 나오는 것을 확인할 수 있습니다.

혹은, 저주파 필터를 직접 간단하게 테스트 할 수 있는 코드는 아래와 같습니다.

class Sensor(object):
    def __init__(self):
        self.value = 10
        self.i = 0

    def noise(self):
        return random.randint(-10, 10) * 0.01

    def sense(self):
        self.i += 0.05
        return math.sin(self.i) + self.noise()


if __name__ == "__main__":

    xs = []
    sensors = []
    filters = []

    lpf = LowPassFilter(3., 0.1)
    sensor = Sensor()

    for i in range(200):
        z = sensor.sense()
        f = lpf.filter(z)

        xs.append(i)
        sensors.append(z)
        filters.append(f)

    plt.plot(xs, filters)
    plt.scatter(xs, sensors, c="r", s=1)

    plt.show()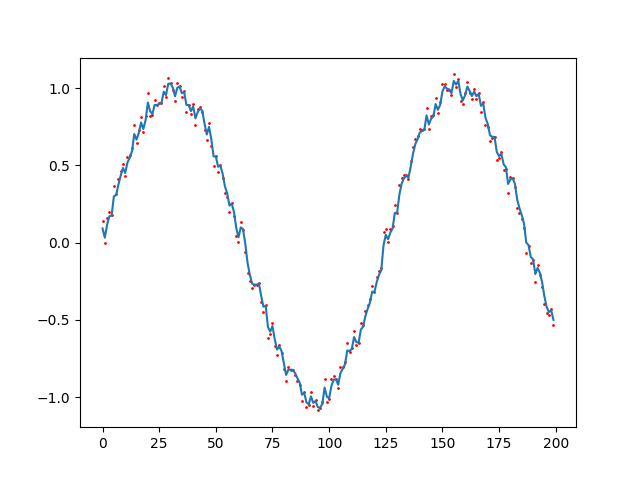

정상적으로 노이즈가 포함된 사인파를 추종하는 것을 확인할 수 있습니다. 여기서 주의해야 할 점이, 차단 주파수(cut off frequency)값의 설정인데, 차단 주파수가 낮을수록, 즉 더 많은 영역의 주파수를 거를 경우에 그래프의 개형은 더욱 매끄럽게 나타나지만, 너무 심할 경우에는 아래처럼 데이터가 심각하게 왜곡될 수 있습니다.

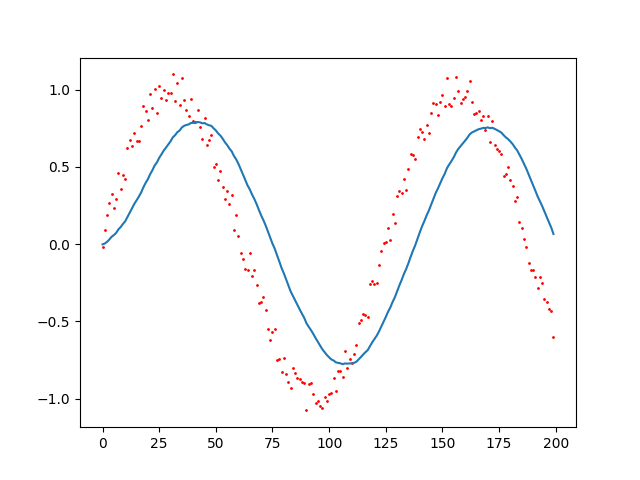
따라서 차단 주파수를 다르게 설정하면서 적절한 차단 주파수를 찾는 작업이 중요하니 참고하시길 바랍니다.