선형 칼만 필터의 이해

칼만 필터란?

칼만 필터(Kalman Filter)는 센서 데이터에 내재된 노이즈나 불확실성을 고려하여, 시스템의 실제 상태를 추정하는 알고리즘이다. 특히 시간에 따라 변화하는 동적 시스템에서, 관측값만으로는 알 수 없는 내부 상태를 수학적으로 추정하는 데 매우 효과적이다.

---

왜 칼만 필터가 필요한가?

간단한 예시를 통해 살펴보자.

1차원 공간을 등속으로 이동하는 자동차가 있다고 가정하자. 시간 간격 $dt$마다 속도 센서로부터 측정한 속도 $v_t$를 이용해, 자동차의 위치는 다음과 같이 계산할 수 있다:

이 식은 이론적으로 맞지만, 실제 속도 센서는 노이즈가 포함된 값을 제공한다. 즉, 센서가 1.0 m/s라는 값을 출력하더라도, 실제 속도는 1.0 m/s 전후의 임의의 값일 수 있다. 이 오차가 누적되면, 위치 추정 결과에 드리프트(누적 오차)가 발생하게 된다.

드리프트 오차

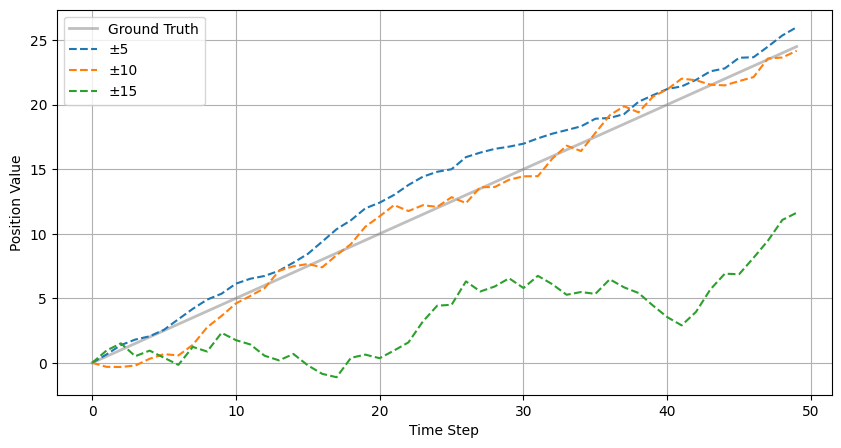
아래 그림은 속도 노이즈가 위치 추정에 어떤 영향을 미치는지 보여준다.

• 회색 실선은 이상적인 경우다. 속도 센서가 정확하게 5.0 m/s를 측정할 수 있다면, 위치는 정확히 예측된다.

• 파란색 점선 (0.0~10.0 m/s), 주황색 점선 (-5.0~15.0 m/s), 초록색 점선 (-10.0~30.0 m/s)은 각각 센서 노이즈 범위가 증가했을 때의 위치 추정 결과를 보여준다. 노이즈가 커질수록 추정 위치는 실제 위치에서 더 크게 벗어난다.

상태와 측정값을 가우시안 분포로 취급하기

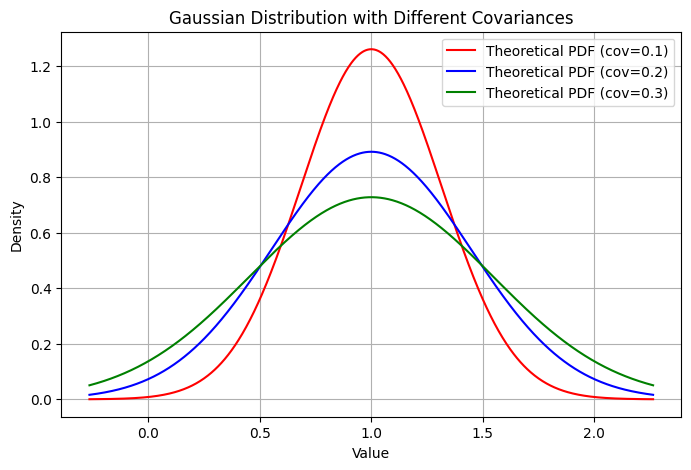
선형 칼만 필터는 시스템의 상태(state)와 측정값(measurement) 모두를 가우시안 확률 분포로 모델링한다. 이는 시스템이 가진 불확실성을 수학적으로 정량화하기 위함이다.

---

예를 들어, 위의 드리프트 오차의 예시와 같이 실제 속도가 5.0 m/s인 상황에서, 센서가 노이즈의 영향으로 0.0~10.0 m/s 사이의 값을 반환한다고 하자. 이 경우 속도 측정값은 다음과 같은 정규 분포로 모델링할 수 있다:

이는 평균이 5.0이고 분산이 8.333인 1차원 정규 분포를 의미한다.

칼만 필터에서는 상태를 일반적으로 다차원 벡터로 표현한다. 예를 들어 위치와 속도를 동시에 추정하는 경우 상태 벡터는 다음과 같다:

이러한 상태의 불확실성은 공분산 행렬(covariance matrix)로 표현된다:

• $Var(position)$: 위치 추정의 분산
• $Var(velocity)$: 속도 추정의 분산
• $Cov(position, velocity)$: 위치와 속도 간의 상관성

공분산 행렬은 상태 간의 오차 상관관계까지 포함하여 시스템의 전체적인 불확실성을 보다 정확하게 표현한다.

---

선형 칼만 필터의 구조

칼만 필터는 시스템의 상태(state)와 그 불확실성(covariance)을 바탕으로 상태를 예측하고, 측정값을 통해 보정하는 순환적 추정 알고리즘이다.

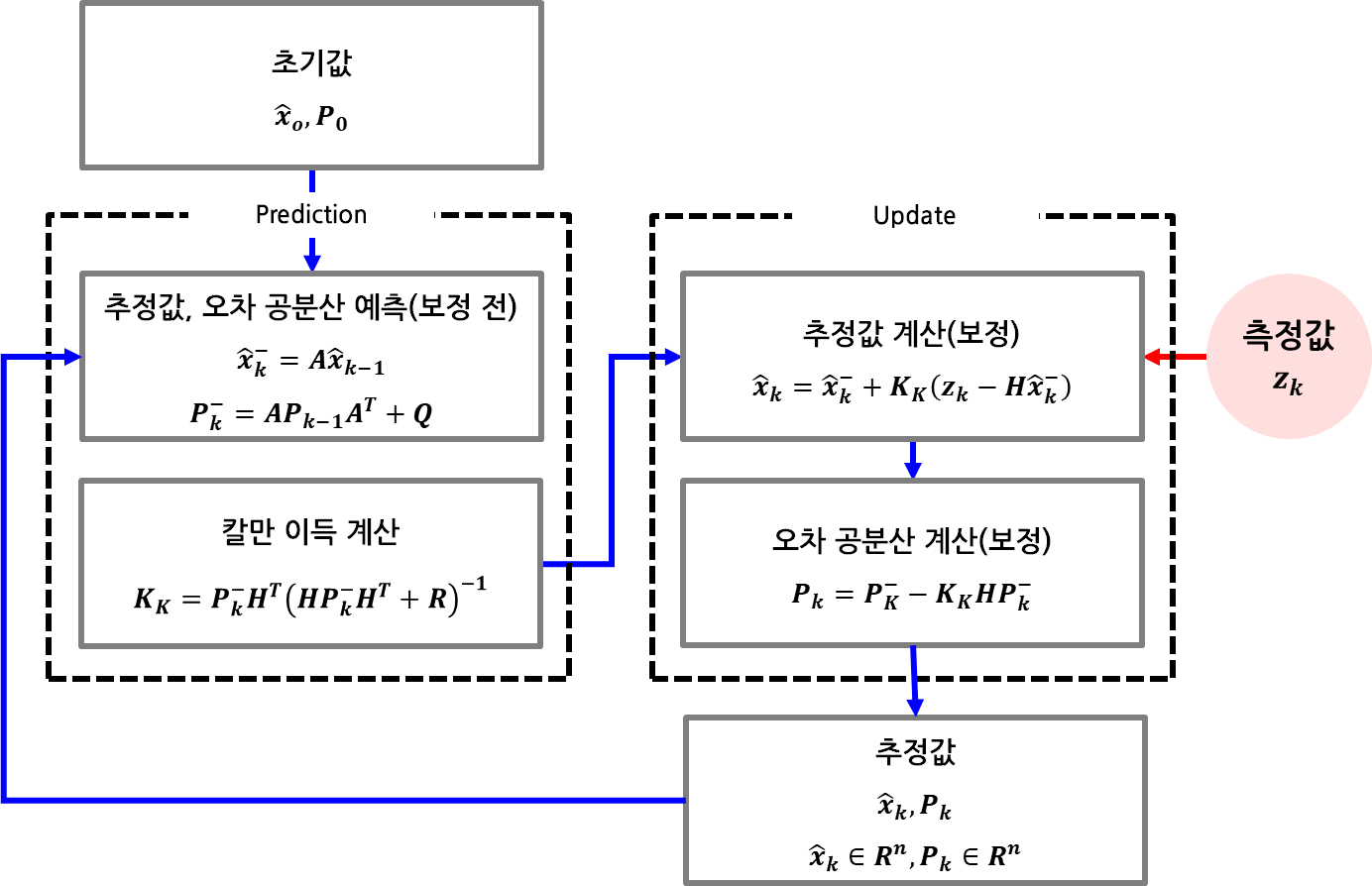
선형 칼만 필터의 핵심 개념은 예측(prediction)과 갱신(update)이다.

현재 시스템 상태와 시스템 모델을 사용하여 다음 상태를 예측하고, 측정값을 통하여 예측한 상태를 보정하는 것으로 다음 스탭의 상태를 추정하는 것이다.

예측(Prediction) 단계

예측 단계에서는 이전 상태와 시스템 모델을 바탕으로, 다음 시점의 상태와 그 오차 범위(공분산)를 추정한다.

---

상태 벡터 예측

예를 들어, 위치($p$)와 속도($v$)를 추정하는 시스템이라면, 다음 상태는 아래처럼 모델링된다:

이 모델을 행렬로 표현하면 다음과 같다:

• 상태 벡터 $x = \begin{bmatrix} p \\ v \end{bmatrix}$

• 상태 전이 행렬 $A = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix}$

칼만 필터에서는 이 식을 통해 예측 상태 $\hat{x}_k^-$를 계산한다:

• 기호 $\hat{x}$: 추정값
• 윗첨자 "-": 보정 전 상태

---

공분산 행렬 예측

시스템 상태의 불확실성 역시 시간에 따라 변화하므로, 공분산도 함께 예측해야 한다. 이를 위해 아래의 오차 공분산 전파식을 사용한다:

• $P_{k-1}$: 이전 상태의 오차 공분산

• $A$: 상태 전이 행렬

• $Q$: 프로세스 노이즈 공분산 행렬

시스템 모델 $A$는 시스템의 상태 벡터가 시간에 따라 어떻게 변화하는지 표현하는 행렬이 되며, 프로세스 노이즈 공분산 행렬 $Q$는 시스템 모델이 완벽하지 않기 때문에 발생하는 모델링 오류나 외란을 반영하는 노이즈 행렬이다.

따라서 이 수식은 $P_{k-1}$이 시스템 모델 $A$에 의해 시간적으로 어떻게 전파(propagate) 되는지를 계산하고, 노이즈 $Q$를 더하는 구조를 가지고 있다.

---

보정(update) 단계

보정 단계(Update)는 예측 단계에서 얻은 상태 추정값과 공분산을 실제 센서 측정값을 통해 수정하는 과정이다. 이 단계의 핵심은 칼만 이득(Kalman Gain)이라는 가중치를 사용하여 예측과 측정 사이의 최적 조합을 산출하는 것이다.

---

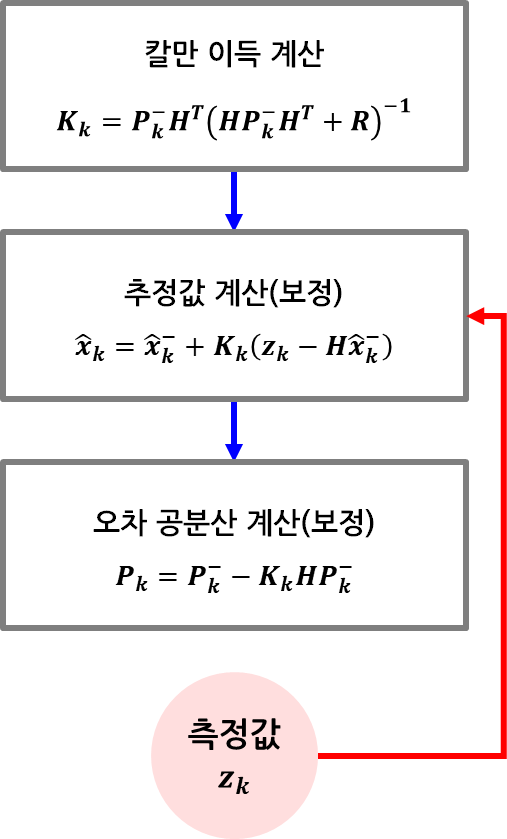
상태 추정값 보정

예측값 $\hat{x}_k^-$과 측정값 $z_k$를 바탕으로, 보정된 상태 추정값 $\hat{x}_k$는 다음과 같이 계산된다:

• $K_k$: 칼만 이득 (Kalman Gain)
• $H$: 관측 행렬 (Observation Matrix)
• $z_k - H \hat{x}_k^-$: 측정 오차 (Innovation)

관측 행렬 $H$는 측정값 $z_k$와 상태 벡터 $x$의 차원을 같게 만들어주는 변형 행렬을 의미하여, 칼만 이득 $K_k$는 측정 오차 $z_k - H \hat{x}_k^-$에 부여되는 가중치이다.

이 수식은 예측된 상태에 측정 오차에 비례한 보정량을 더하여, 보다 신뢰도 높은 상태를 추정하는 구조를 가진다.

---

칼만 이득 계산

칼만 이득은 다음과 같은 수식으로 정의된다:

• $R$: 측정 잡음 공분산 행렬

칼만 이득은 칼만 필터가 상태 추정 오차의 제곱 평균값을 최소화하기 때문에, 보정 후 공분산 행렬 $P_k$의 trace를 최소화 하도록 설계된 값이다.

칼만 이득의 자세한 유도 과정은 아래와 같다:

넘기기

---

1. 상태 오차 정의

상태 오차 $e_k$는 다음과 같이 정의한다:

측정 오차 $z_k - H \hat{x}_k^-$에 선형 측정 모델 $z_k = H x_k + v_k$에 대입한다:

• $v_k$: 측정 노이즈

이를 상태 오차 $e_k$에 대입한다:

2. 오차 공분산 전개

오차 공분산 행렬 $P_k$는 아래와 같이 전개할 수 있다:

3. 크로스 항 제거

여기서 예측 오차 $x_k - \hat{x}_k^-$는 측정 노이즈 $v_k$와 서로 관계가 없는 독립적인 값임으로 $𝔼[(x_k - \hat{x}_k^-)v_k^T] = 0$로 하여 오차 공분산 행렬 $P_k$를 단순화 한다:

• $𝔼[(I - K_k H) (x_k - \hat{x}_k^-) K_k^T v_k^T]$ = 0
• $𝔼[K_k v_k (x_k - \hat{x}_k^-)^T (I - K_k H)^T]$ = 0

따라서

이 식은 보정 후 상태 오차 공분산을 정확히 나타낸다.

4. Trace 최소화

오차 공분산 $P_k$를 trace를 통해 스칼라로 변환한다:

5. 그래디언트 최소 조건

$P_k$의 trace를 최소화하는 $K_k$를 찾는다:

이를 $K_k$에 대하여 정리하여 최적의 칼만 이득을 유도한다:

오차 공분산 보정

위에서 정의한 오차 공분산 $P_k$을 전개한다:

2차 항 및 고차 잡음 항을 생략하여 근사적으로 단순화한다:

$Thus,$

요약

정리하자면, 이와 같은 과정을 통하여 Update 단계에서는 다음과 같은 단계를 거치게 된다.

1. 칼만 이득 계산

2. 추정값 보정

3. 상태 오차 공분산 보정

---

시스템 차원

선형 칼만 필터의 시스템은 위의 과정을 반복하는 것으로 마무리된다. 여기에 추가적으로 칼만 필터에서 사용하는 변수들의 차원을 정리하여 이해를 돕고자 한다.

시스템 상태를 표현하는 값

• 상태 벡터 $x$: 시스템의 현재 상태를 정의
• 오차 공분산 행렬 $P$: 상태 벡터의 "정확도"를 의미하는 오차 공분산
• 시스템 잡음 행렬 $Q$: 시스템의 예측 과정에서 발생하는 추가적인 오차 공분산 행렬

상태 벡터는 사용자가 정의하는 크기($n$)를 가지는 벡터가 되며, 오차 공분산 행렬은 상태 벡터와 같은 크기를 가지는 정방행렬이 된다.

측정을 표현하는 값

• 측정 벡터 $z$: 외부 계측 값을 정의
• 측정 잡음 공분산 행렬 $R$: 측정 벡터의 "정확도"를 의미하는 잡음 공분산
• 관측 행렬 $H$: 외부 계측 값과 상태 벡터의 차원을 맞추는 변환 행렬

시스템 행렬

• 상태 전이 행렬 $A$: 시스템의 예측에서 상태 벡터의 전이 방법을 정의하는 행렬

---

센서 퓨전과 칼만 필터

칼만 필터는 노이즈가 포함된 관측값으로부터 시스템의 상태를 추정할 수 있을 뿐만 아니라, 복수의 센서 데이터를 통합(fusion)하여 더욱 정밀한 상태 추정이 가능하다는 장점을 가진다.

이것이 가능한 이유는 칼만 필터에서 사용하는 상태 벡터($x$)와 측정 벡터($z$)의 차원이 고정되어 있지 않고, 필터 설계자가 시스템에 맞게 정의할 수 있기 때문이다.

---

단일 센서 기반 시스템

처음에 든 예시와 같이 1차원 공간을 등속으로 이동하는 물체의 위치(position)와 속도(velocity)를 추정하고, 센서로는 속도만 측정할 수 있다고 하자. 이 경우 시스템은 다음과 같이 정의된다:

복수 센서 기반 시스템

이제 여기에 가속도(acceleration) 센서를 추가한다고 가정하자. 그러면 추정하고자 하는 상태에 가속도를 포함시킬 수 있으며, 측정값 또한 속도와 가속도 두 가지로 확장된다.

---

결론

칼만 필터는 다음과 같은 이유로 센서 퓨전에 매우 적합한 구조를 갖고 있다:

• 상태 벡터 $x$의 정의는 유연하며, 필요에 따라 추정하고자 하는 물리량을 자유롭게 확장할 수 있다.

• 측정 벡터 $z$ 역시 센서 구성에 따라 조정 가능하며, 여러 센서의 정보를 하나의 필터로 통합할 수 있다.

• 행렬 $A$, $H$, $Q$, $R$ 등은 상황에 맞게 설계 가능하므로 다양한 물리 시스템에 대응할 수 있다.

---

샘플 코드 (python)

1. 상태 정의 클래스

• predict: 칼만 필터의 예측(prediction) 과정을 구현
• update: 칼만 필터의 보정(update) 과정을 구현

class KalmanState(object):
    def __init__(self):
        self._x = np.array([0.0, 0.0])  # [position, velocity]
        self._P = np.eye(2) * 5.0  # Large initial uncertainty

    def predict(self, A: np.ndarray, Q: np.ndarray) -> np.ndarray:
        """Predict the next state."""
        self._x = A @ self._x
        self._P = A @ self._P @ A.T + Q

        print(f"Predicted state: {self._x.flatten()}")
        print(f"Predicted covariance: {np.linalg.det(self._P)}")

        return self._x.flatten()

    def update(self, H: np.ndarray, R: float, z: np.ndarray) -> np.ndarray:
        """Update the state with a new measurement."""
        y = z - (H @ self._x)  # Measurement residual
        S = H @ self._P @ H.T + R  # Residual covariance
        K = self._P @ H.T @ np.linalg.pinv(S)  # Kalman gain using pseudo-inverse

        # Update state and covariance matrix
        self._x += K @ y
        self._P = self._P - K @ H @ self._P

        print(f"Updated state: {self._x.flatten()}")
        print(f"Updated covariance: {self._P}")

        return self._x.flatten()

    @property
    def x(self) -> np.ndarray:
        return self._x

    @property
    def P(self) -> np.ndarray:
        return self._P

2. 칼만 필터 클래스

• A, Q, H, R: 시스템 행렬을 정의
• filter: 칼만 필터의 예측-보정 과정을 구현

class KalmanFilter(object):
    def __init__(
        self,
        dt: float = 0.1,
        process_noise: float = 0.1,
        measurement_noise: float = 0.1,
    ):
        assert dt > 0.0, "dt must be positive"
        assert process_noise > 0.0, "process_noise must be positive"
        assert measurement_noise > 0.0, "measurement_noise must be positive"

        self._num_steps = 50

        self._dt = dt
        self._process_noise = process_noise
        self._measurement_noise = measurement_noise

        self._measurements = np.random.uniform(-10.0, 30.0, self._num_steps)
        std = np.std(self._measurements)

        # State transition matrix
        self.A = np.array([[1.0, dt], [0, 1.0]])

        # Process noise covariance matrix
        self.Q = np.eye(2) * process_noise

        # Measurement matrix
        self.H = np.array([[0.0, 1.0]])  # Measurement matrix for velocity

        # Measurement noise covariance matrix
        self.R = np.array([[std**2.0]])

        # Initial state estimate and covariance matrix
        self.state = KalmanState()

    def filter(self, z: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:
        """Perform a Kalman filter step."""
        # Predict the next state
        x_pred = self.state.predict(self.A, self.Q)

        # Update the state with the new measurement
        x_upd = self.state.update(self.H, self.R, z)

        return x_pred, x_upd

    def run(self):
        """Run the Kalman filter on a set of measurements."""
        # Simulate some measurements (e.g., velocity)
        print(f"Measurements: {self._measurements}")

        # Store predictions and updates for plotting
        predictions = []
        updates = []

        for z in self._measurements:
            z_vec = np.array([z])
            pred, upd = self.filter(z_vec)
            predictions.append(pred)
            updates.append(upd)

        return np.array(predictions), np.array(updates)

    @property
    def measurements(self) -> np.ndarray:
        return self._measurements

3. 실행 결과

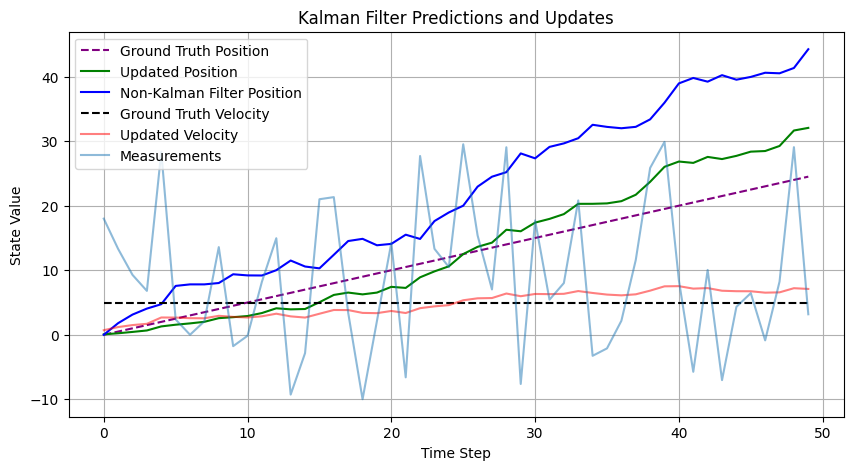
10.0~20.0 dt마다 Random Velocity 생성: $\mu=10.0$, $\sigma^2=133.33$

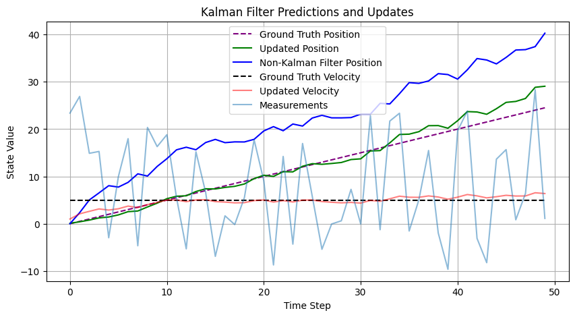
칼만 필터를 적용한 위치/속도 추정

• (초록색 실선) 칼만 필터로 추정한 위치
• (빨간색 실선) 칼만 필터로 추정한 속도

칼만 필터를 적용하지 않은 위치/속도 확인

• (파란색 실선) RAW 속도로 추정한 위치
• (하늘색 실선) 랜덤 샘플링 한 RAW 속도

노이즈가 적용되지 않은 위치/속도 확인

• (점선) 고정된 5.0 속도 상황에서 위치/속도

---

참고 문헌

• 칼만 필터 - 위키피디아
• 선형 칼만 필터의 원리 이해 - JINSOL KIM
• 칼만 필터는 어렵지 않아 (김성필)

---

끗. 배고프다.