비지도학습 :
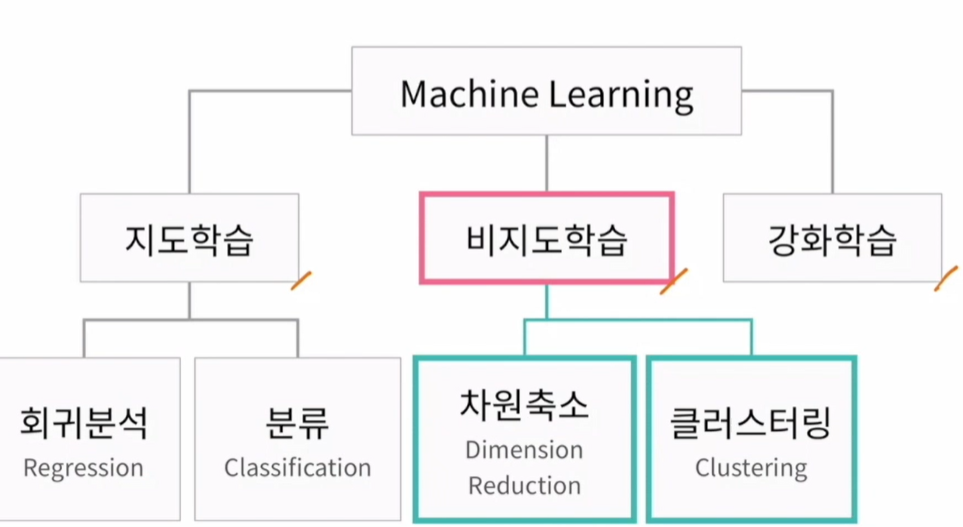
회귀분석 : 알고이거나 예측하기 위한 값. 키가 주어졌을때 몸무게 예측. 선형.
분류 : 클래스 같은 것 나누는 것. 새로운 것이 왔을 때 어떤 클래스인가. 나이브베이즈.
비지도 : 값이 없어도 할 수 있는것.
지도학습 : 얻고자 하는 답으로 구성된 데이터
비지도학습 : 답이 정해져 있지 않은 데이터에서 숨겨진 구조를 파악. 데이터들이 가진 특성으로 컴퓨터가 분류. 뭐가 뭐인지는 모르겠지만 뭉쳐있다는 것을 찾아내는 것.
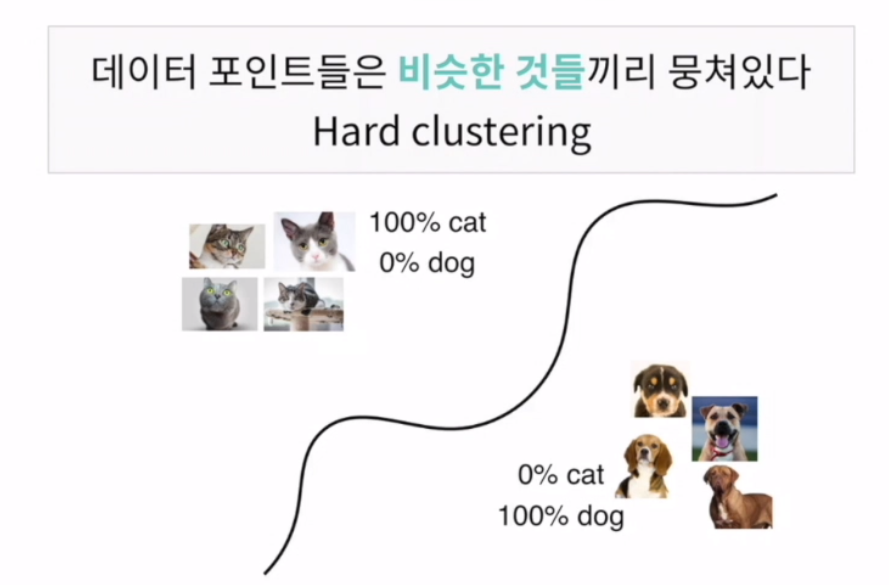
hard clustering
데이터 포인트들은 비슷한 것들끼리 뭉쳐있다
한 개의 데이터 포인트는 숨겨진 클러스터들의 결합이다
60% 강아지, 40% 고양이 인 친구는 없음. 선을 딱 그어줌
K-MEANS
soft clustering
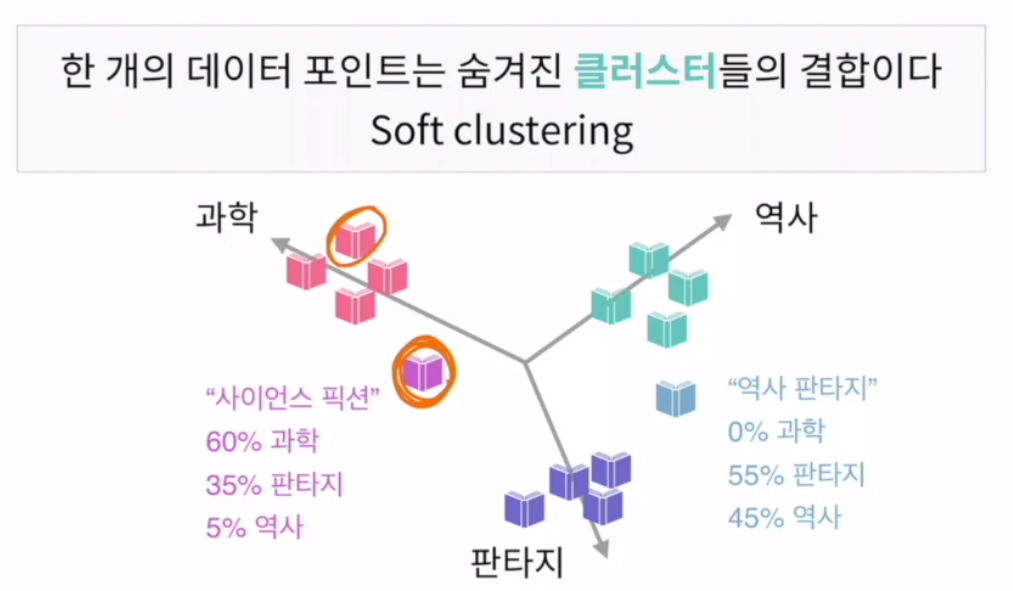
책은 주제 중의 여러개가 들어있음. 그래서 클러스트링이 확실히 나눠지지 않음.
각각의 클래스가 0이나 1이 아닌 값으로 구성. 60% 역사 40% 판타지
GMM 가우시안믹스쳐모델(EX) 자연적인 것은 대부분 소프트 클러스트링이 많음
일반적으로 많이 사용해야하지만 어려워서 하드클러스트링 사용하는 경우가 많음
HARD
목표 : 비슷한 데이터 포인트끼리 모은다
이 때 클러스터 2개를 찾아줘! 2개 = K
사람이 하나의 클러스터가 뭘 의미하는지는 찾아줘야됨. 컴퓨터는 값을 모을 뿐.
K결정하기
완벽한 방법은 없음
1. 눈으로 확인
2. 모델이 얼마나 잘 설명하는가. 계속 값을 넣어보면서
고려할 것들
- 데이터의 특성 : 어떻게 만들어진 데이터인가, 데이터 포인트 외 다른 FEATURE
- 분석결과로 얻고자 하는 것 : 고양이 VS 개 / 사람들의 행동 분석 : 논문에서 5개로 나누더라(사전지식) / 가격 대비 효율성 분석
하지만 이렇게 사전지식이 없을 때는? 차원축소
EX
와인 분석하기. 엘리스 와이너리에서는 수백개 와인을 생산했고 생산팀은 와인들에 대한 13가지 특성을 측정해서 정리함.
문제 : 178개 정도의 와인들을 몇가지로 분류할 수 있겠는가?
가장 쉬운 것은 눈으로 보는 것이지만 13가지 특성을 13차원으로 온전히 볼 수 없음. 그래서 2차원 혹은 3차원으로 줄여야함. 그것이 바로 PCA.
PCA 주성분분석
왜사용해? 1. 고차원의 데이터를 저차원으로 줄이기 위해(예 : 시각화)
2. 데이터 정제 . 관찰 장비나 측정에 관해 노이즈가 생김. 3차원으로 나왔는데 이게 사실 실수가 자명하다면? 2차원으로 정제. 시각화보다는 정제에 더 많이 사용됨. 기계적으로 데이터 간 거리를 측정하면 되기 때문에. 너무 특성이 많으면 나누기 어렵기 때문에 필요한 애들만 뽑아봄.
-> 필연적으로 데이터 손실이 일어나는데 그것을 줄여야 함
k-means
기계학습 중 제일 쉬울듯ㅎ
주어진 데이터를 비슷한 그룹(클러스터)로 묶는 알고리즘
컴퓨터에게 줘야하는 값은 k. 몇 개의 클러스터로 나눠줄지 알려줘야함.
ex.
위에서 나눈 pca를 통해 그림을 만들어놨음. 이제 이걸 3개의 브랜드로 나눌텐데 어떤 와인을 어떤 브랜드에 할당할지 판단해야 함.
반복을 이용한 클러스터링 알고리즘.
1. 중심 : centroid. 각 클러스터의 중심
2. 중심과의 거리 : distance. 중심과 데이터 포인트와의 거리
거리는 일반적으로 norm으로 정의 중심이 가장 중요.
처음에는 중심값을 데이터 중 임의로 설정. 중심값이 정해지면 각각의 데이터 포인트에 대해 다음을 계산. 내게서 가장 가까운 중심정은 어디인지 norm으로 정함. 나머지 데이터 포인트에 대해 동일한 작업을 계속 수행. 그래서 가까운쪽에 데이터를 할당. 1차적으로 할당. 정해진 클러스터에서 중심점을 다시 게산. 중심점은 해당 클러스터 내 데이터 포인터 위치의 무게중심 혹은 평균.
그래서 새로운 중심을 만들어냄. 다시 반복. 새로운 중심에 대해 모든 포인터들을 다시 클러스터링. 그럼 다시 할당. 또 반복. 또 반복. 중심점을 계속 업데이트하면서 계속 반복. 다시 할당. 언제까지 반복하냐면 중심 업데이트를 계속 하다가 어떠한 데이터 포인트가 클러스터에 속한 곳이 변하지 않을 때.
