담당교수: 서울대학교 협동과정 인공지능전공 교수 이원종

Definition of Unspervised Learning

기계 학습의 일종으로, 지도학습 또는 강화학습과는 달리 입력 목표치가 주어지지 않아 데이터가 어떻게 구성되었는지를 알아내는 문제의 범주에 속한다.

Traditional Ways of Unsupervised Learning

K-means Clustering

K-means Clustering이란, Unlabeled dataset에 대해 해당 데이터셋에 대해 일정한 K개의 데이터 군집으로 군집화시키는 것을 의미한다. 이때 점들의 군집을 클러스터라고 하는데 이 클러스터는 점들의 모임으로 다른 군집들과는 구별된 모습을 보인다. 이러한 데이터에 대한 클러스터를 진행할 경우, 데이터세트에 대해 알맞은 최적화 변수들이 필요한데 이를 클러스터의 중심으로 표현한다. 추가로 클러스터에 해당하는지에 따라서 Binary의 1과 0이 결정된다.
K-means Clustering의 MSL Loss Function은 E(t,mu) = Sum^{N}{n=1} Sum^{N}{n=1}t_nk|x_n-mu_k|^2
으로 계산되며 이러한 MSL를 줄이기 위해서는 다음과 같은 두가지 과정을 반복적용하여 나타낼 수 있다.
1. Assign x_n to closest Cluster. t_nk will be taken by sign results of k, which is arg min|x_n-mu_j|^2.
2. Minimize E with respect to mu_k by fixing t_nk.
다음과 같이 반복 적용시 Centroid of datapoints는 Cluster k에 할당되어 수렴하게 된다.

Other Unsupervised Learning Methods

Hirarchical Clustering

Hierarchical Clustering의 의미도 K-means Clustering과 매우 유사하게 작동한다. 다만 우리가 K-means Clustering에 대해 Centroid와의 거리를 측정한 후에 그냥 그대로 두었다면, Hierarchical에서는 가장 가까운 점들에 대해 구분관계를 설정하여 가까운 점에서 먼 점끼리 도식화시킬 수 있다는 점이 있다.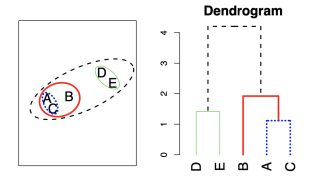

Density Estimation

Density Estimation도 근본적인 Basis를 가지는데 예를 들어서 아래와 같은 -4~8의 데이터 파라미터 아래에 많은 Dirac Function이 있다고 가정할 때, 가장 많은 Dirac Function을 가지는 구획에 대해 Scalar 갓으로 표현할 수 있다.

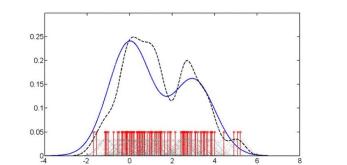
PCA

PCA는 차원을 줄이기 위한 방식이다. 주로 다차원 데이터를 시각화하는데 사용되며 벡터 이미지의 크기를 조정하는데에 도움을 주기도한다. 이러한 특성으로 인해 고차원 데이터 집합에서 패턴을 찾는데에 도움을 주며 선형대수에서 찾아볼수 있는 Eigenvalue Decomposition(대각화 행렬)과 동일한 방식을 취한다.

Relationship with these Traditional Machine Learning

이러한 전통적인 머신러닝에 대한 공통점은 낮은 차원 데이터와 단순 컨셉트에 대해 다루었다는 것이고 다만 클러스터링 과정에서 검증이 매우 필요한 점을 이해하여야 했다. (Internal, External, Relative)

Unsupervised Learning in Deep Learning

Feature Engineering in the Traditional Standard Perceptron Architecture

전통적인 방식에서의 데이터의 가공을 통해 모델의 성능을 높이는 방법은 입력에 대해 사용자가 직접적으로 편향, 편중값을 넣어주어서 이를 구현되는 단위에 대한 알고리즘을 통해 성능향상을 제어하는 방법이었다.

Typical Prediction Problem

Ordinary Prediction

전통적인 방식에서, 역시 일반적으로 Observation Data X에 대해 f라고 하는 Prediction Model을 통해 조절된 값인 y를 배출하는 것이 일반적인 Framework임

Typical Prediction Problem

• Observation data X로부터 prediction model f를 잘 찾는 것이 목표인데, y라는 정보에서 Data generation process(non-linear)를 통해 X라는 데이터가 됨. 이러한 f가 x에서 필요한 정보 y를 잘 뽑을 수 있도록 해내는 것을 Feature Engineering이라고 한다.
• 그렇기 때문에 Deep learning은 우리가 Feature engineering을 하고 있는 부분을 알고리즘을 통해 y를 출력할 수 있도록 하는 것이라고 할 수 있다. 이때의 학습방법을 Representation Learning이라고 한다.

Modern Unsupervised Learning

• High dimensional data(image, language)
• Difficult concepts : Not well understood, but surprisingly good performance
  -> Deep learning, Unsupervised Representation Learning
• Representation이라는 것은 정보를 어떤 식으로 정리/표현할 것인가에 대한 것으로 상당히 중요하고 성능이 잘 나오는데 큰 영향을 끼치므로 인간이 많이 도와줄 필요가 있음.

Representation Learning in Deep Learning

Deep Neural Networks

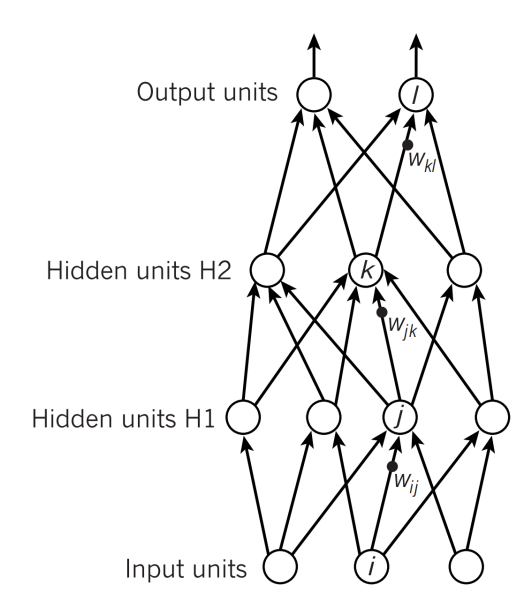
과정: input layer에서 어떤 경우엔 Time Complexity에 대해 불리한 상황이거나 잘 처리를 못하는 경우에는 Hyperparametre와 같은 추가적인 도움을 통해서 도와주어야 한다.
이러한 경우를 Heavy pre-processing이라고 하며 이에 대해 세 가지 방식으로 구분할 수 있다.

• Heavy Preprocessing: 인간이 가장많이 도와주는 경우
• Minimum Preprocessing: 대비정규화와 같이 최소한의 도움을 받아 진행하는 경우
• No preprocessing: 그냥 생 데이터를 가지고 진행하는 경우

최상부의 경우(output layer)에는 Output representation에 대해 인간이 디자인하여 쓰고 있으며 Softmax Function이라던가, One-hot encoding이라던가 확률적인 예상을 사용한 개념들에 대해 디자인하여 나타낸다.

Middle layer에 대해 Activation Vector에 대해 아직은 생각하기가 어려우며 그렇기 때문에 Good Representation이 무엇인지는 정리하기가 어렵다.