Causal Effect Identifiability

Causal Effect Identifiablity is confirmed from three objects; Query Px(y) = P(y|do(x)), Causal Diagram, and the Data P(V). By these components, we can make the Causal Inference Engine's object to this statement.

Based on the current knowledge about the phenomenon and the available data, is the research question identifiable?

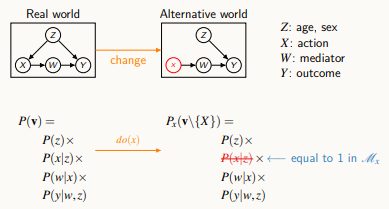
If the solution answer is yes, it becomes formula Px(y) = fG(P(V)); otherwise it becomes to an evidence. Also, the calculated image changes into

While the process is ongoing, the distribution decomposes as P(V) = P(Sl|W) P(W|Sp,R) P(Sp|Sn)P(R|Sn)P(Sn). It may representated as

The causal effect Q = P(y|do(x)) is identifiable whenever X,Y,PaX ⊆ V (all parents of X) are measured. The expression of Q is then obtained by adjustment for P(paX), or P(y|do(x)) = ∑_{paX} (P(y|x,paX)P(paX).

Adjustment Formulas

Whether Season is latent or not, The effects are still computable, in a way of Adjustment Formulas. As shown on the upper statement, with the formula below, the effects are still computable.

∑{sn,r} P(W | Sp = on,r)P(sn)P(r|sn) or ∑{r} P(W | Sp = on,r)P(r)

Back-door Criterion

Back-door Criterion is a way that helps you know the concept. By finding a set Z such that it can sufficiently explain the wrong-ness between X and Y then it could be explained with

P(y|do(x)) = ∑_{z} P(y|x, z)P(z)

If a set Z satisfies the back-door criterion with respect to a pair of variables X, Y in a causal diagram G if; 1. no node in Z is a descendant of X; and 2. Z blocks every single passage between X-Y notation. Here is an example shown before the post (Take a look on Causality Section) Another reason of wet - but not sprinkler - is shown with blue colour(Rain). With this section, we can also make a graphical condition for Back-door Admissible Sets.

Do-calculus

Backdoor criterion results in a very specific form of identification, and Do-Calculus provides general machinery to control observational and interventional distributes.
(Lv1. Associational <> Level 2 Experimental) Do-calculus is sound and complete but it has no algorithmic insight. But a graphical condition and an efficient algorithmic procedure have developed for identifiability.

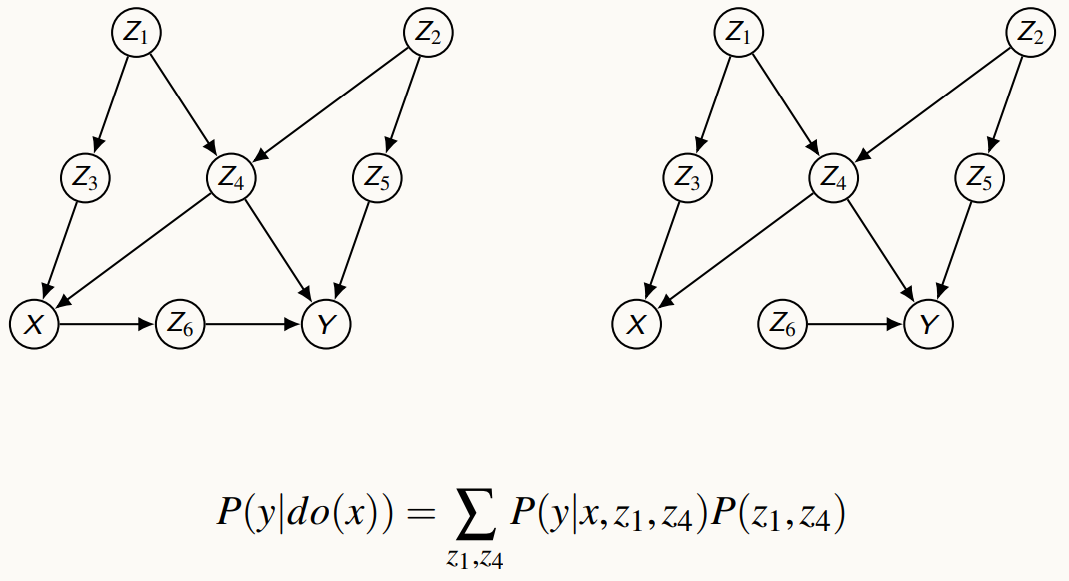
The following images show the Rules and Action Results of Do-calculus.

Rules of Do-calculus

Do calculus in Action