With the diversity of various Data sources, the modern identificaiton tasks are divided into four conditions; For Experimental Conditions, Generalized Identification is applied. For Environmental Conditions, Transportability is the main concept. For Sampling conditions, Recovering from the selection bias is important. Finally for respondent conditions, recovering from missingness is a vital theme.
Generalized Identification
Case with heightened cholesterol level
We can all say that heightened Cholesterol Levels may derive Heart Attack. Exercise, however, cures(or prevents) both Cholesterol Level AND Heart Attack. So, we can measure by both measurement methods, the Observational one - (P(X,Y,Z)), and the Experimental one - (P(X,Y)|do(Z)).
Case with Drug-Drug Interactions
You are an doctor prescribing medicines for patients(I don't know why they took the "Drug" term in). There is high/low blood pressure and this phenomenon makes a cardiovascular disease. You can give him antihypertensive drug, or anti-diabetic drug, or well, both of them.
Getting General Identifiability with Calculus
Our goal is to assess the effecto fo prescribing both treatments on the risk of diseases from individual experiments, eiither antihypertensive one or anti-diabetic one.
Following the statements, we can calculate the identifiability like this.
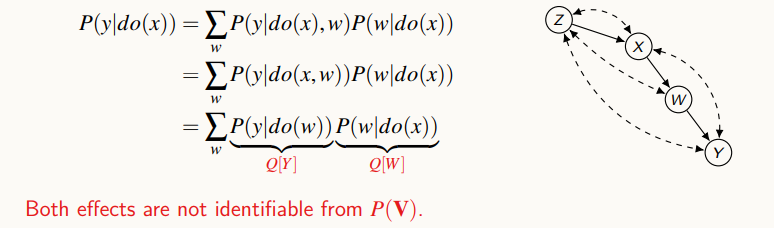

From this method, the identifiability of any expression of the form can be determined given any causal graph G and an arbitrary combination of observational and experimental studies. If the query is identifiable, with polynomial time the estimation can be derived.
Transportability
Can we port the system on other software set?
Even if we have a perfect RCT, the system cannot be easily transported to another system. However, non-parametric transportability can be determined provided that the problem instance is encoded in selection diagram. When transportability is feasible, the transport formula can be derived in polynomial time, and the causal calculus and the correspondent algorithm are complete.
Recovering from Selection Bias
Survivorship bias
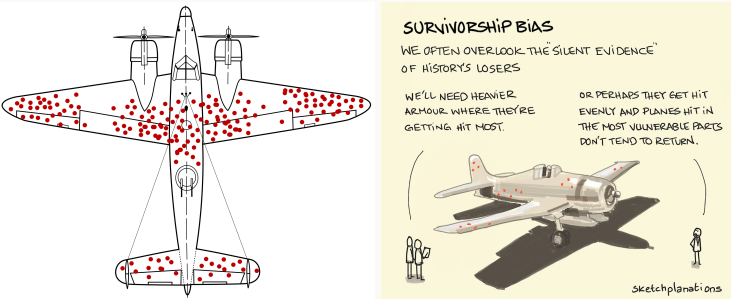
The survivorship bias stands for the de Havilland Mosquito plane that survived from the NSDAP planes. The U.S. army (since there were no U.S.A.F. that time)tried to reinforce the red dot parts but instead armored the non-red parts to their upgrades.
Selection bias, which is caused by preferential inclusion s of samples form the data below is a major obstacle to both valid causal and statistical inferences, as shown below.
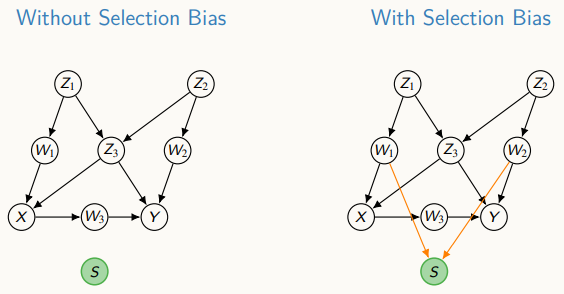
Without External Information, the Theorem is explained as
Q = P(y|x) is recoverable from selection biased data if and only if (S ㅛ Y | X).
However with the External Data, Indentification under Selection can be evaluated as
P(y|x) is recoverable if there is a set C such that (Y ⊥⊥ S | C,X) holds in G and P(C,X) is estimable. Moreover, P(y|x) = ∑_{c} P(y|x, c,S = 1)P(c|x)
For example, this is a good example of Selection.

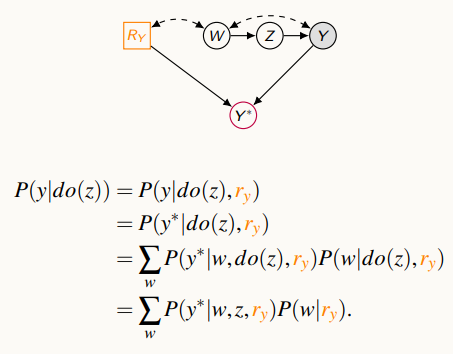
Recovering from Missing Data
Consider a study conducted an identification poll, but somewhat datas are missing. Modelling the missingness process using obseity O, missingness mechanism Ro, and a proxy variable O* is needed.
Missingness can be caused by random processes or depend on other variables. There are three factors can be found, but can be calculated mathematically, like this.