D+15 통계학 기초! 그래프 개념 정리 & 시각화 실습
오늘 공부한 것:
- 통계학 기초 챕터 3 강의 듣고 실습해보기!
- 프로그래머스 sql 19문제 풀기! (정답률 높은 문제)
- 파이썬 라이브 세션 챕터 2까지 이해하기!
오늘 슬랙에 우수 TIL 선정이 발표가 나왔는데,
그걸 보면서 아.. 남는 건 TIL뿐이지 않을까 라는 생각이 들었다.
사실 나는 TIL (Today I Learned)을 벨로그에 업로드하고,
외부 시간엔 개인 노트에 TIL과 TIT(Today I tried)를 적어서
주말마다 적은 개념을 누군가에게 설명할 수 있도록 공부했다.
개념과 문법을 익히는 데에는 큰 도움이 된 게 확실했다.
근데 외부로 노출시키는 게 아니라서
내가 잘 하고 있다는 걸 타인에게도, 나에게도
증명할 방법이 없다고 느꼈다.
그래서 앞으로 우수 TIL로 선정될 수 있도록
내가 겪은 우여곡절도 TIL에 빡빡하게 담아 제출하려고 한다.
모집단과 표본
- 모집단: 관심 대상이 되는 전체 집단 ex) 한 국가의 모든 성인
- 표본: 모집단에서 추출한 일부 ex) 국가의 성인 중 일부 조사
표본을 사용하는 이유
- 비용과 시간
- 접근성
대표성
- 표본의 대표성:
잘 설계된 표본은 모집단의 특성을 반영할 수 있음.
이를 통해 표본에서 얻은 결과를 모집단 전체에 일반화 O,
데이터 관리
- 데이터 처리의 용이성:
전체 데이터를 다루는 것보다 데이터 처리 & 분석이 용이함 - 데이터 품질 관리:
작은 표본에서는 데이터 품질을 더 쉽게 관리하고, 오류나 이상값을 식별하여 수정할 수 있음.
모델 검증 용이
- 모델 적합도 테스트:
표본 데이터를 사용하여 통계적 모델을 검증할 수 O
모델이 표본 데이 터에 잘 맞는다면,
모집단에도 잘 맞을 가능성 높음
파이썬 실습!!!
import numpy as np
import matplotlib.pyplot as plt
# 모집단 생성 (예: 국가의 모든 성인의 키 데이터)
population = np.random.normal(170, 10, 1000)
# 표본 추출
sample = np.random.choice(population, 100)
plt.hist(population, bins=50, alpha=0.5, label='population', color='blue')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='red')
plt.legend()
plt.title('population and sample distribution')
plt.show()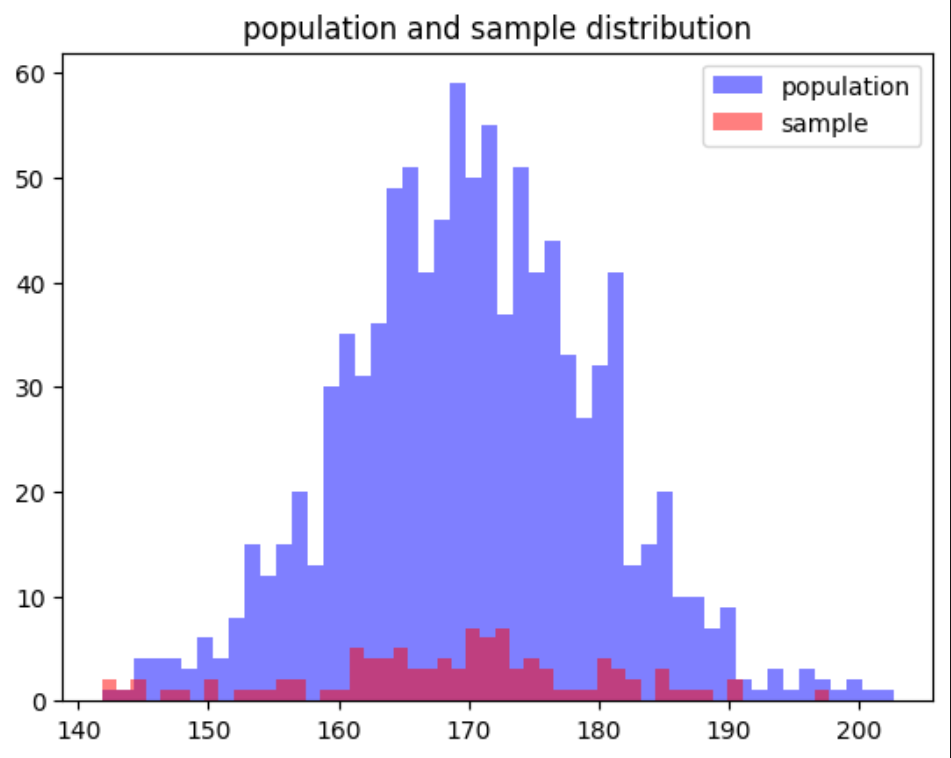
numpy.random이 뭘까?
- Numpy 라이브러리의 일부.
- 다양한 확률 분포에 따라 난수를 생성하는 기능 제공.
- 사용 분야: 데이터 분석, 시뮬레이션 방법 등등
np.rnado.normal
- 함수는 정규분포를 따르는 난수를 생성.
- 정규분포는 평균과 표준편차를 중심으로 데이터가 대칭적으로 분포하는 분포.
코드 설명:
numpy.random.normal(loc=0.0, scale=1.0, size=None)
loc(float): 정규 분포의 평균 (기본값: 0.0)scale(float): 정규분포의 표준편차 (기본값: 1.0)size(int 또는 tuple of ints): 출력 배열의 크기 (기본값: None. 즉, 스칼라 값 반환)
np.random.choice
- 주어진 배열에서 임의로 샘플링하여 요소를 선택.
- 지정된 배열에서 무작위로 선택된 요소를 반환하는 기능 제공.
코드 설명:
numpy.random.choice(a, size=None, replace=True, p=None)
a(1-D array-like or int): 샘플링할 원본 배열. 정수인 경우np.arange(a)와 동일하게 간주.size(int 또는 tuple of ints): 출력 배열의 크기
(기본값: None, 즉 단일 값 반환)replace(boolean): 복원 추출 여부를 나타냄.
True면 동일한 요소가 여러 번 선택될 수 있음. (기본값: True)p(1-D array-like, optional): 각 요소가 선택될 확률.
배열의 합은 무조건 1.
pit.hist가 뭘까?
- Matplotlib 라이브러리에서 히스토그램을 그리는 함수. 히스토그램은 데이터의 분포를 시각화하는 데 유용한 도구.
- bins
- 히스토그램의 bins의 개수 또는 경계.
- 데이터 몇 개의 구간으로 나눌 것인지에 대한 것.
- 정수나 리스트로 입력 가능.
정수: 빈의 개수 지정.
리스트: 각 빈의 경계를 직정 지정. (130~140, 140~160 리스트로 작성)
- alpha
- 히스토그램 막대 투명도 지정. 0(투명) -> 1(불투명) 사이 값.
- label
- 히스토그램의 레이블 지정. 여러 히스토그램 그릴 때 범례 추가하는 데 사용.
- color
- 히스토그램 막대 색상 지정.
표본 오차와 신뢰구간
! 표본이 모집단 대비 얼마나 차이나는지, 신뢰 가능성 파악 !
표본 오차
- 표본에서 걔산된 통계랑 & 모집단의 진짜 값 간의 차이
- 표본 크기가 클수록 표본 오차는 작아짐.
- 표본이 모집단을 완벽하게 대표하지 못하기 때문에 발생.
표본의 크기와 표본 추출 방법에 따라 달라질 수 있음.
표본의 크기: 표본의 크기가 클수록 표본 오차는 줄어듦.
더 많은 데이터를 수집할수록 모집단을 더 잘 대표하게 됨.
표본 추출 방법: 무작위 추출 방법 사용 -> 표본오차 줄일 수 O .
모든 모집단 요소가 선택될 동등한 기회를 가지게 해야 함.
신뢰 구간
- 모집단의 특정 파라미터(ex: 평균, 비율)에 대해 추정된 값이 포함될 것으로 기대되는 범위를 나타냄.
신뢰구간 계산 방법
신뢰구간=표본평균±z×표준오차
여기서 z는 선택된 신뢰수준에 해당하는 z-값.
예를 들어, 95% 신뢰수
준의 z-값은 1.96임
일반적으로 95% 신뢰수준을 많이 사용.# 포본 오차, 신뢰구간 그림으로 확인

- 모집단 표본 분포 (왼쪽)
- 붉은 점선 = 모집단 평균, 파란 점선: 표본 평균
- 모집단 분포는 넓고, 표본 평균의 분포는 좁아짐.
- 표본 크기가 커질수록 표본 평균이 모집단 평균에 가까워지는 경향.
- 신뢰구간 시각화 (오른쪽)
- 표본 분포와 95% 신뢰구간을 보여줌.
- 파란 점선 = 표본 평균,
녹색 점선 = 95% 신뢰구간의 상한과 하한. - 신뢰구간은 모집단 평균을 포함할 것으로 예상되는 범위임.
파이썬 실습!!
수학 점수 표본으로부터 모집단의 평균 범위 계산
import scipy.stats as stats
# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)
# 95% 신뢰구간 계산
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, sca
print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")stats.t.interval란 뭘까?
scipy.stats는 SciPy 라이브러리의 일부.- 통계 분석을 위한 다양한 함수와 클래스들을 제공하는 모듈.
scipy.stats.t.interval함수는 주어진 신뢰 수준에서
t-분포 사용 -> 신뢰 구간 계산하는 데 사용.
scipy.stats.t.interval(alpha, df, loc=0, scale=1)
- alpha
신뢰 수준을 의미. 예를 들어, 95% 신뢰 구간 을 원하면
alpha를 0.95로 설정.
- df
자유도를 나타냄. 일반적으로 표본 크기에서
1을 뺀 값으로 설정. df = n - 1
- loc
위치. 일반적으로 표본 평균을 설정.
- scale
스케일. 일반적으로 표본 표준 오차 설정. 표본 표준 오차는 표본 표준편차를 표본 크기의 제곱근으로 나눈 값.
scale = sample_std / sqrt(n)
정규 분포
!!!!!!!! 가장 대표적인 분포 !!!!!!!!
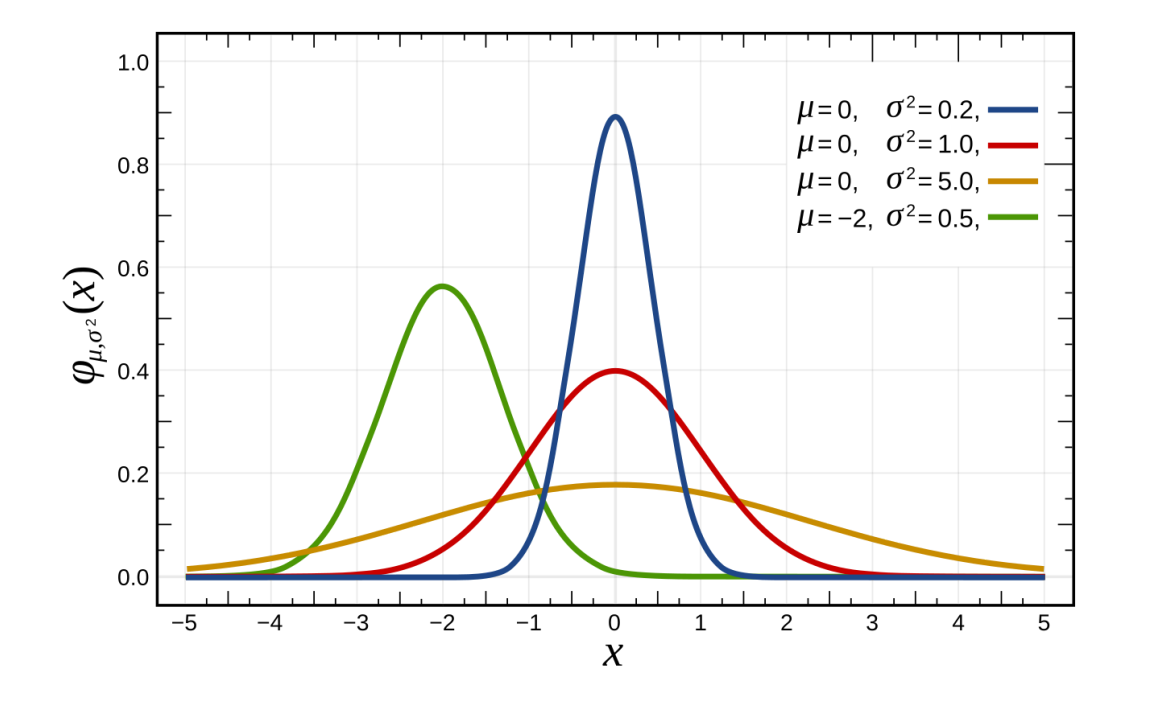
정규 분포
- 정규분포는 종 모양 대칭 분포.
- 대부분의 데이터가 평균 주위에 몰려 있는 분포.
- 평균을 중심으로 좌우 대칭.
- 평균에서 멀어질수록 데이터 빈도 감소.
- 표준편차는 분포의 퍼짐 정도를 나타냅니다.
특징
대부분의 데이터가 평균 주변에 몰려 있음.
평균에서 멀어질수록 빈도는 줄어듦.
파이썬 실습!!!
# 정규분포 생성
normal_dist = np.random.normal(170, 10, 1000)
# 히스토그램으로 시각화
plt.hist(normal_dist, bins=30, density=True, alpha=0.6, color='g')
# 정규분포 곡선 추가
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, 170, 10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('normal distribution histogram')
plt.show()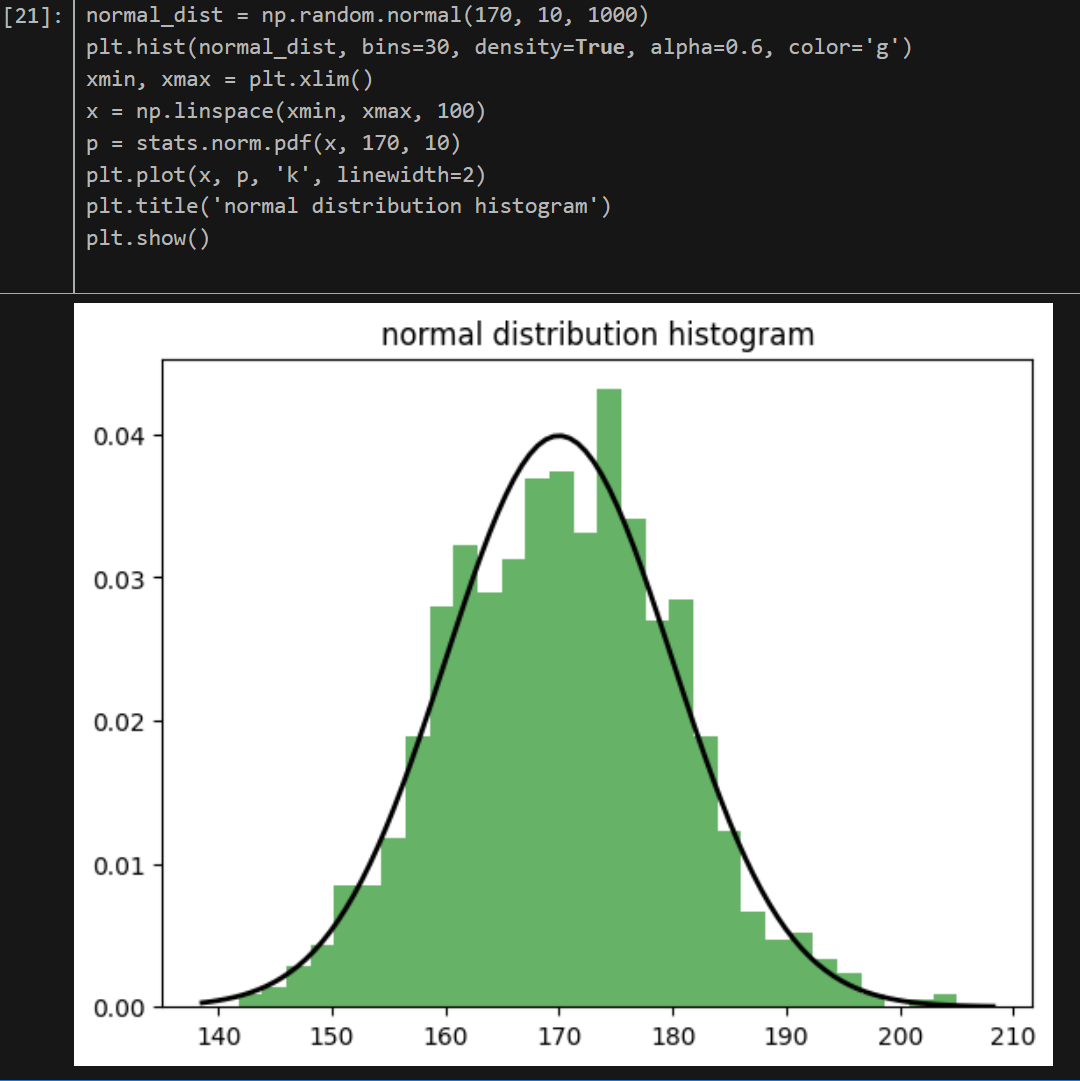
긴 꼬리 분포
!! 데이터가 비대칭적으로 꼬리 형태로 분포할 때 사용 !!
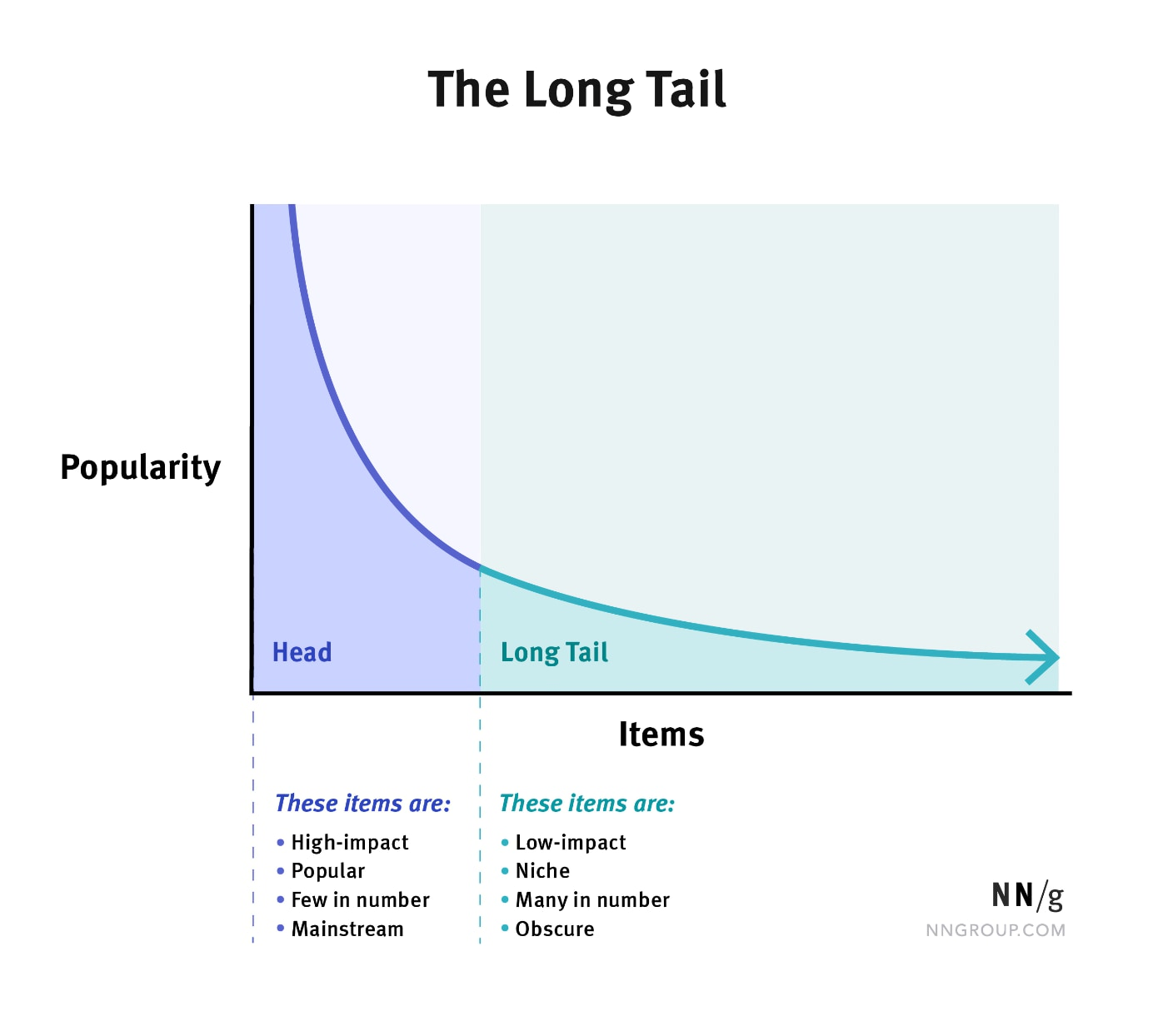
긴 꼬리 분포
- 긴 꼬리 분포는 대부분 데이터가 분포 한 쪾 끝에 몰리고, 반대쪽으로 긴 꼬리가 이어지는 분포
- 이는 정규분포와 달리 대칭적이지 않고 비대칭적입니다.
- 특정 하나의 분포를 의미하지 않고, 여러 종류의 분포
(예: 파레토 분포, 지프의 법칙, 멱함수)를 포함할 수 있음.
특징
- 소득 분포, 웹사이트 방문자 수 등에서 관찰됨.
!! 파이썬 실습 !!
long_tail = np.random.exponential(1, 1000)
plt.hist(long_tail, bins=30, density=True, alpha=0.6, color='b')
plt.title('long tail distribution histogram')
plt.show()
!! 혼자 뚝딱뚝딱 학습해보기 !!
1. 히스토그램 시각화 연습
모집단 기준: 성인 남녀 각각의 평균과 표준편차 설정
남성: 평균 175cm, 표준편차 7cm
여성: 평균 162cm, 표준편차 6cm
시각화 기준
성인 남녀의 키 데이터를 각각 정규 분포로 만들고,
한 눈에 볼 수 있도록 겹쳐서 시각화
도전 1
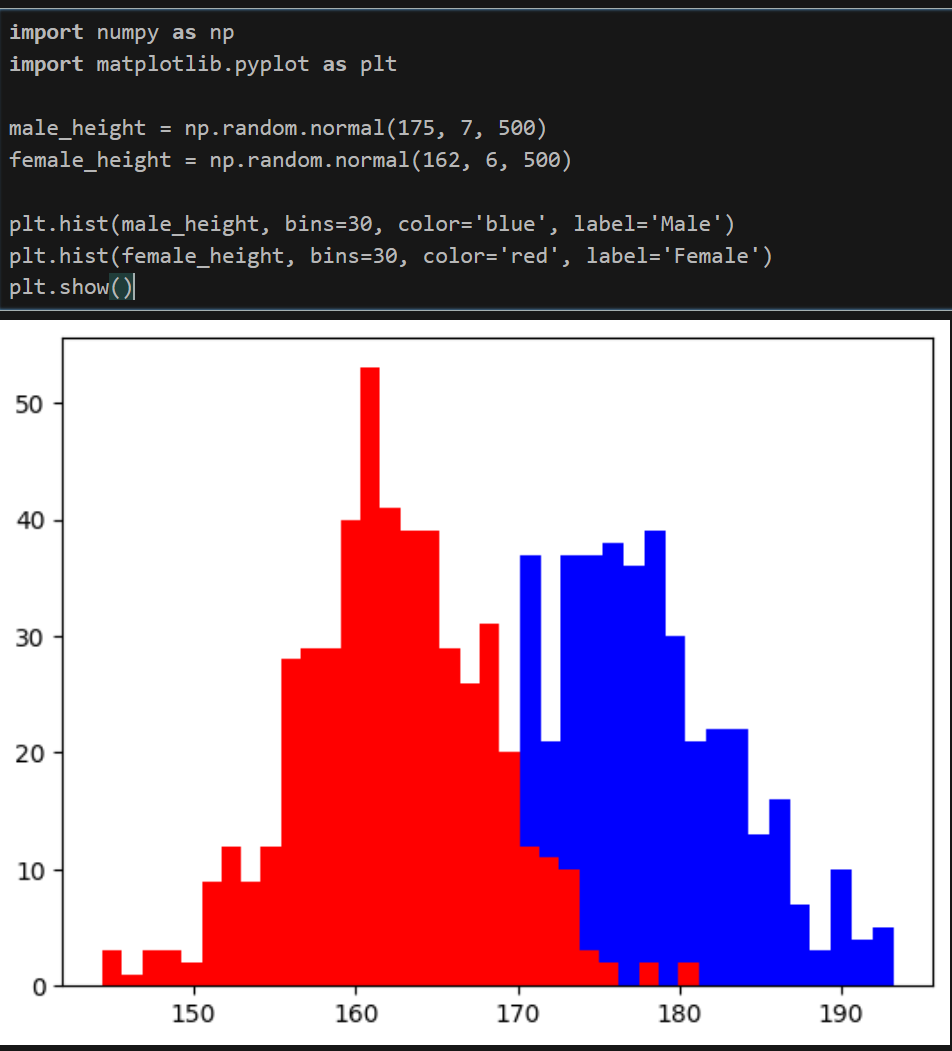
문제 1: 투명도(겹침의 문제)
구체적 문제: 170cm 이하인 남성의 키를 알 수 없음.
생각: alpha 값을 이용해 투명도를 조절.
plt.hist(male_height, bins=30, alpha=0.5, color='blue', label='Male')
plt.hist(female_height, bins=30, alpha=0.5, color='red', label='Female')문제 2: 레이블과 범례
구체적인 문제: 성별 구분이 명확하게 나타나지 않음.
생각: label 각 데이터가 무엇을 나타내는지 구분하도록.
plt.legend() 범례 표시 명령어. 추가 입력
문제 3: 재현 가능성
구체적 문제: 랜덤 데이터를 여러 번 실행하면
결과가 매번 달라서 시각화 비교가 어려움
생각: np.random.seed(42) 추가
문제 4: 그래프 이해도
구체적인 문제:히스토그램만 보면
축과 제목이 없어서 해석 어려움
생각: 제목, x축, y축 라벨 추가
plt.title('Adult Height Distribution by Gender')
plt.xlabel('Height (cm)')
plt.ylabel('Frequency')최종!
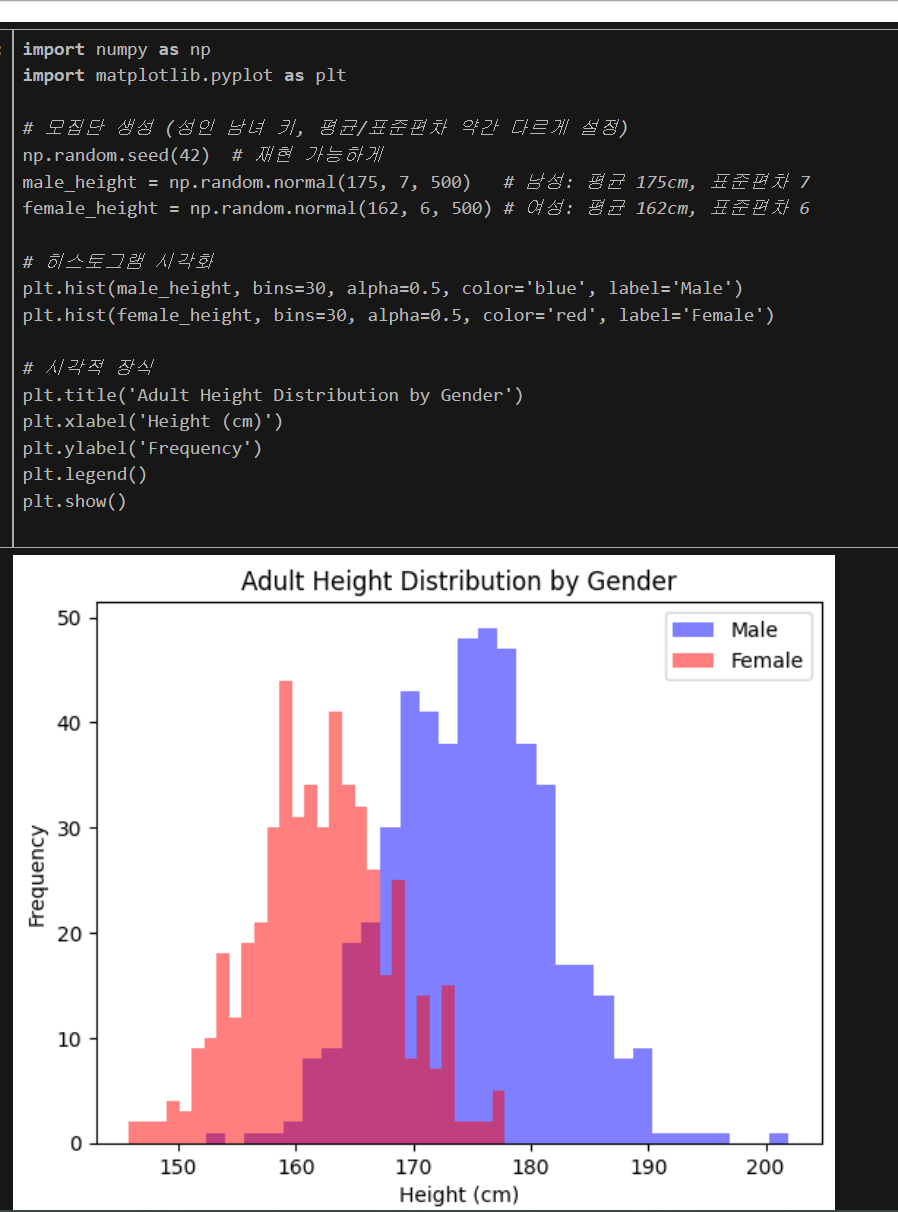
마무리하며
이렇게 보니, 수월하게 푼 것 같지만..
스스로 만든 히스토그램 시각화 완성하기까지
2시간 정도 걸린 것 같다.
비로소 원하는 게 나타났을 때 진심으로 울 뻔 했다,,
뿌듯해서 하룰라라~!@#~#!
오늘 이렇게 꽉 채운 TIL을 작성해봤다.
TIL을 20시~21시 작성하는 게 시간이 많이 촉박할 것 같아서
틈틈히 메모장 켜두고 작성했는데, 딱 알맞게 끝났다.
나름 그동안 해온 TIL보다 훨씬 탄탄하니까
내가 얻는 게 훨씬 많아졌다고 느꼈다.
