DFS 와 BFS

---

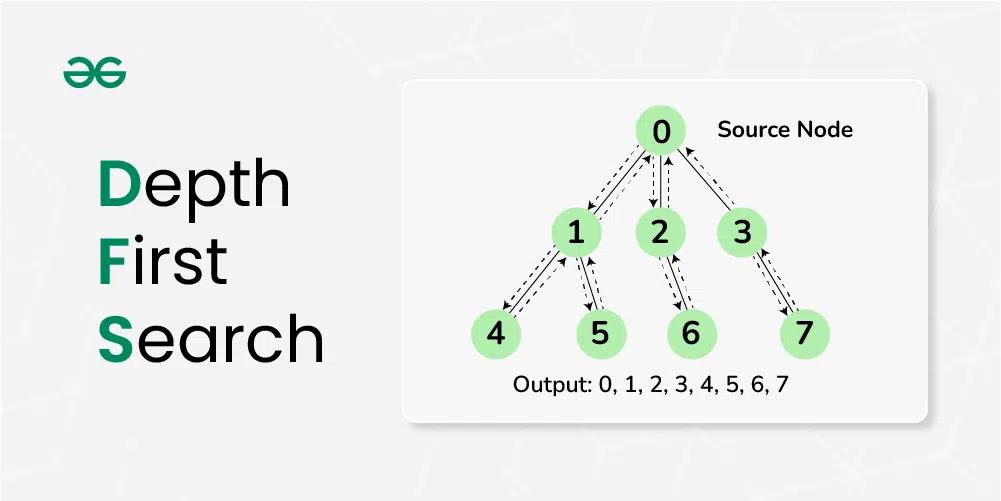
DFS (STACK AND RECURSIVE)

• 시작점에서 갈 수 있는 정점부터 깊이 있게 파고 드는 알고리즘

• 현재 정점과 연결된 정점들을 하나씩 갈 수 있는지 검사하고, 특정 정점으로 갈 수 있다면 그 정점에 가서 같은 행위를 반복한다.(재귀함수 이용) 이때 방문한 곳을 다시 방문하지 않기 위해, 방문한 곳은 표시를 해둔다.

장점

코드가 직관적이고, 구현하기 쉽다.
-> 사실 일정행동을 계속 반복하는데, 이를 만들어놓고 끝까지 계속 돌려 쓰는 것이기 때문에 비교적 간단하게 코드를 구현할 수 있다.

단점

1. 깊이가 엄청 깊어지면, 메모리 비용을 예측하기 어렵다.
   -> 앞서 설명한 것처럼 깊이가 깊어질수록 함수가 하나씩 쌓이는 구조이다. 이 때문에 깊이가 엄청 깊어진다면 스택 메모리가 지나치게 커질 수 있다.
2. 최단 경로를 알 수 없다.

---

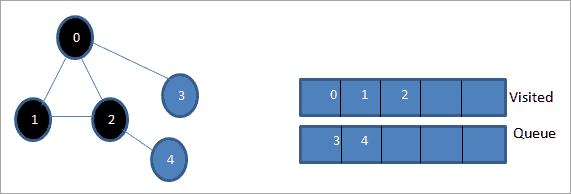
BFS (QUE)

• 가장 먼저 시작 정점을 방문한 후, 그 시작 정점과 인접한 모든 정점들을 우선적으로 탐색해나가는 방법

• 출발점을 먼저 큐에 넣고, 큐가 빌 때까지 아래 과정을 반복한다.

• 큐에 저장된 정점을 하나 Dequeue한다. 그리고 뺀 정점과 연결된 모든 정점을 큐에 넣는다.

장점

1. 비교적 효율적인 운영이 가능하고, 시간/공간 복잡도 면에서 안정적이다.
   -> 깊이 우선 탐색 같은 경우에는 정답을 찾는데,
   바로 구할 수 있는 것도 돌고 돌아서 찾아낼 수 있지만,
   BFS는 그래도 예상한 부분에서 나오게 된다.
2. 최단 경로를 구할 수 있다.

단점

1. 구현이 까다롭다.
2. 모든 지점을 탐색한다는 가정하에 큐에 메모리가 어느 정도 준비돼 있어야 한다.
   -> 정점이 100만개라면, 큐 메모리가 100만개가 준비되어있어야 한다.

Code

DFS for Stack

const dfsForStack = (graph, start, visited) => {
  // 오른쪽부터
  const stack = [start];

  while (stack.length) {
    const v = stack.pop();
    if (!visited[v]) {
      console.log(v);
      visited[v] = true;

      graph[v].forEach((val) => {
        if (!visited[val]) stack.push(val);
      });
    }
  }
};

DFS for recursive

const dfsForRec = (graph, v, visited) => {
  //왼쪽부터 탐색
  visited[v] = true;
  console.log(v);

  graph[v].forEach((val) => {
    if (!visited[val]) dfsForRec(graph, val, visited);
  });
};

const visited = new Array(6).fill(false);
const graph = [[1, 2, 4], [0, 5], [0, 5], [4], [0, 3], [1, 2]];

dfsForStack(graph, 0, visited); // 0 4 3 2 5 1
dfsForRec(graph, 0, visited); // 0 1 5 2 4 3

시작 노드의 값이 1부터 시작하면 visited의 길이는 7로 해야한다. (0-based index)
=> 0부터 시작했으니 6으로 설정해도 무방하다.

BFS

const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A", "G", "H", "I"],
  D: ["B", "E", "F"],
  E: ["D"],
  F: ["D"],
  G: ["C"],
  H: ["C"],
  I: ["C", "J"],
  J: ["I"],
};

const BFS = (graph, startNode) => {
  let visited = []; // A B C D
  let needVisit = [startNode];

  while (needVisit.length) {
    const node = needVisit.shift();
    if (!visited.includes(node)) {
      visited.push(node);
      needVisit = [...needVisit, ...graph[node]];
    }
  }
  return visited;
};

console.log(BFS(graph, "A"));
// A B C D G H I E F H