- 이진트리 (binary tree) 란 ?
- 모든 노드들이 둘 이하(0,1,2 개)의 자식을 가진 트리이다.
- 이진 탐색 트리(Binary Search Tree, BST) 란 ?
- 왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 이진 트리이다.
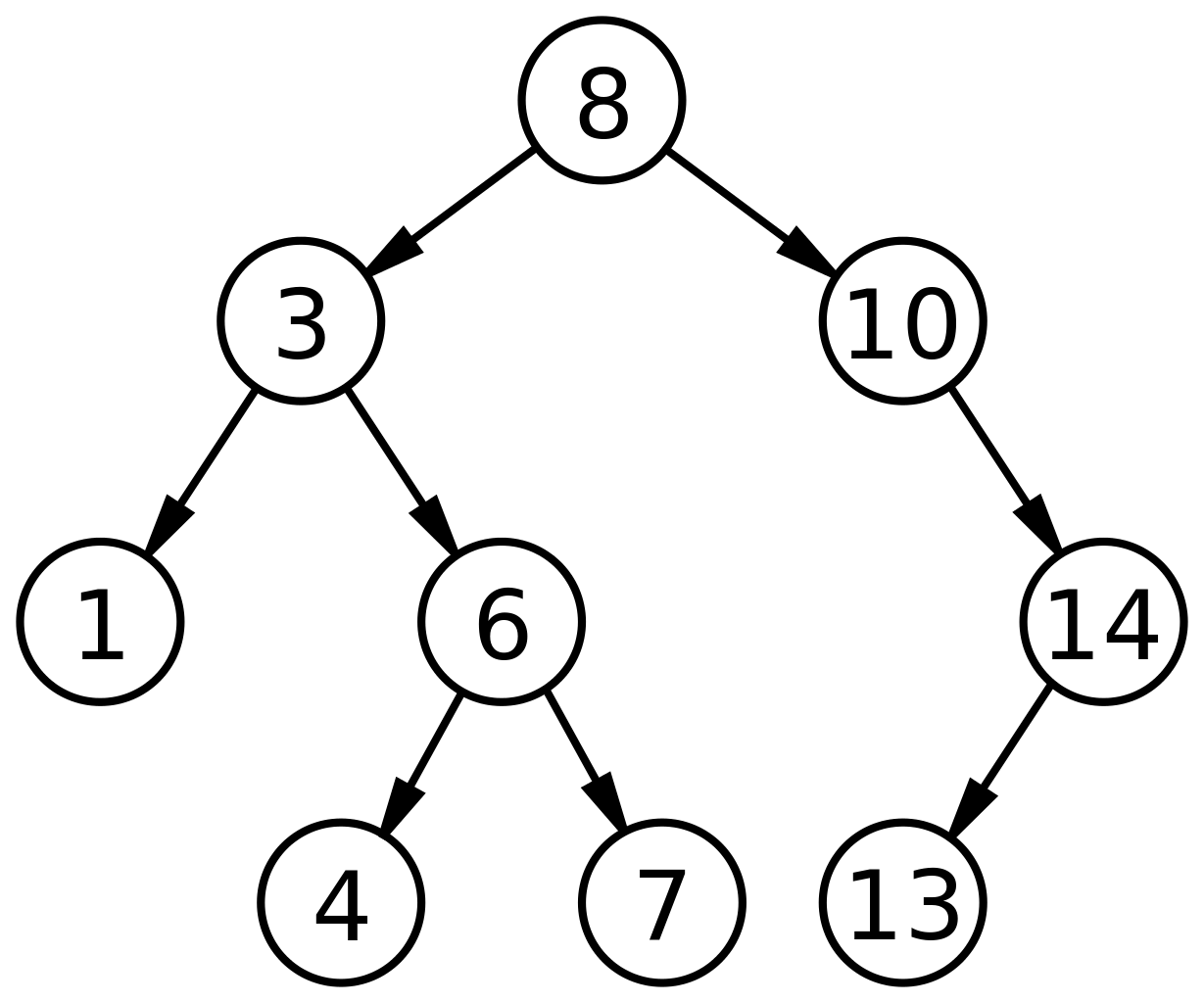
조건
1) 부모 노드의 왼쪽 노드는 부모 노드보다 작아야 한다.
2) 부모 노드의 오른쪽 노드는 부모 노드보다 커야 한다.
-
BST는 삽입, 삭제, 탐색과정에서 모두 트리의 높이만큼 탐색하기 때문에 O(logN)의 시간 복잡도를 가진다.
-
문제는 트리가 편향트리가 되어버렸을 때 결국 배열과 다름 없어지고 시간 복잡도는 O(N)이 된다.
-
중위순회(inorder traversal)를 하면, 오름차순으로 정렬된 순서로 Key값을 얻을 수 있다.
참고로 순회 종류는 아래와 같다.
전위 순회(preorder traverse) : 뿌리(root)를 먼저 방문
뿌리 -> 왼쪽 자식 -> 오른쪽 자식
( 8 -> 1 -> 3 -> 6 -> 4 -> 7 ....)
중위 순회(inorder traverse) : 왼쪽 하위 트리를 방문 후 뿌리(root)를 방문
왼쪽자식 -> 뿌리 -> 오른쪽 자식
( 1 -> 3 -> 4 -> 6 -> 7 -> 8 -> ...)
후위 순회(postorder traverse) : 하위 트리 모두 방문 후 뿌리(root)를 방문
왼쪽자식-> 오른쪽 자식 -> 뿌리
(1 -> 4 -> 7 -> 6 -> 3 -> 13 -> ..)
- 정 이진트리(full binary tree)란?
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다

- 완전 이진트리(complete binary tree)란?
-
마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리이다.
-
마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
완전 이진 트리의 개념은 힙(heap)과 관련이 있다.
- 완전 이진 탐색 트리(Complete binary search tree)란?
- 완전 이진 트리의 성질을 가지는 이진 탐색 트리이다.
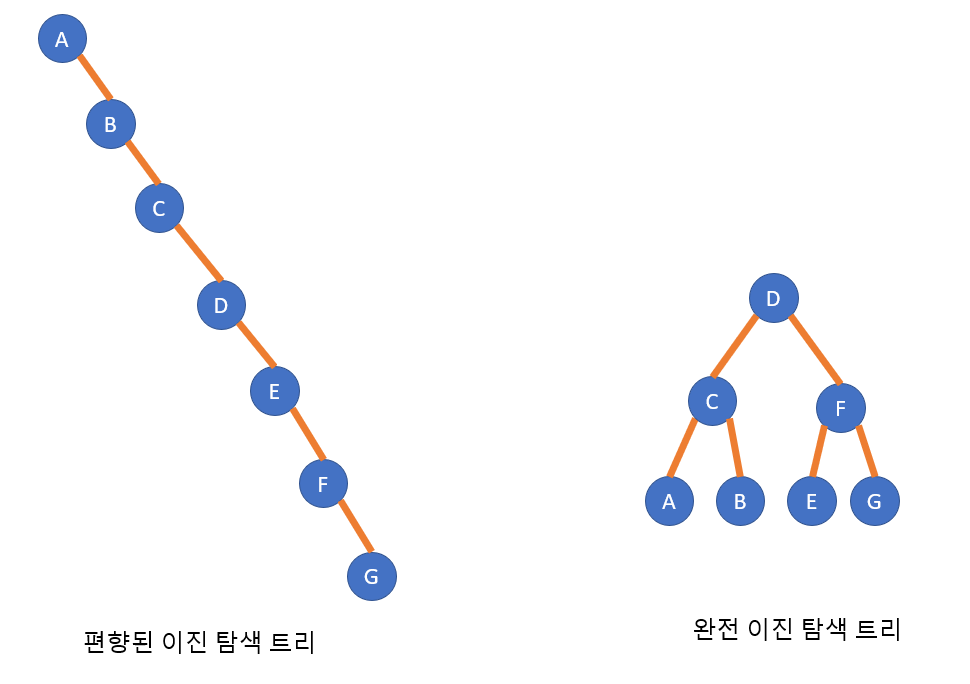
편향된 이진 탐색 트리와 다르게 항상 O(log n)의 검색 속도를 보장한다.
하지만 트리에 자료가 삽입될 때 마다 완전 이진 탐색 트리의 형태를 유지하기 위해
트리의 모양을 바꾸어야 하기 때문에 삽입 시 시간이 많이 소요된다.
따라서 삽입이 적고 탐색이 많은 경우에 유리하며
삽입하는 빈도수가 높아지면 효율성이 떨어지고 이를 해결한 것이 AVL트리이다.
- 포화 이진 트리 (Perfect Binary Tree)
- 정 이진 트리이면서 완전 이진 트리인 경우이다.
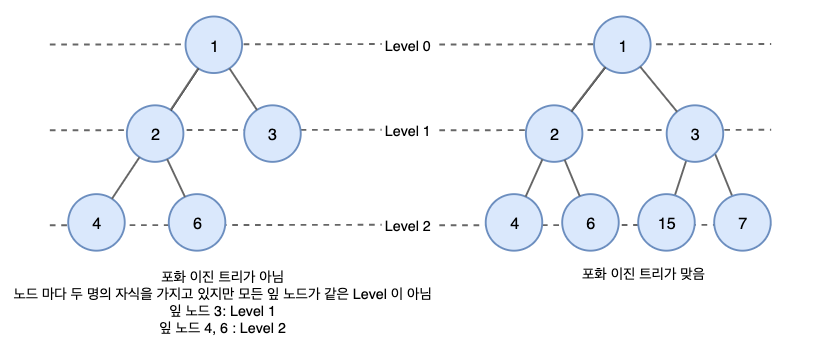
모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리이다.
즉, 모든 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는다.
