백준 1193번 분수찾기

핵심) 계차수열의 특성을 이용하였습니다.

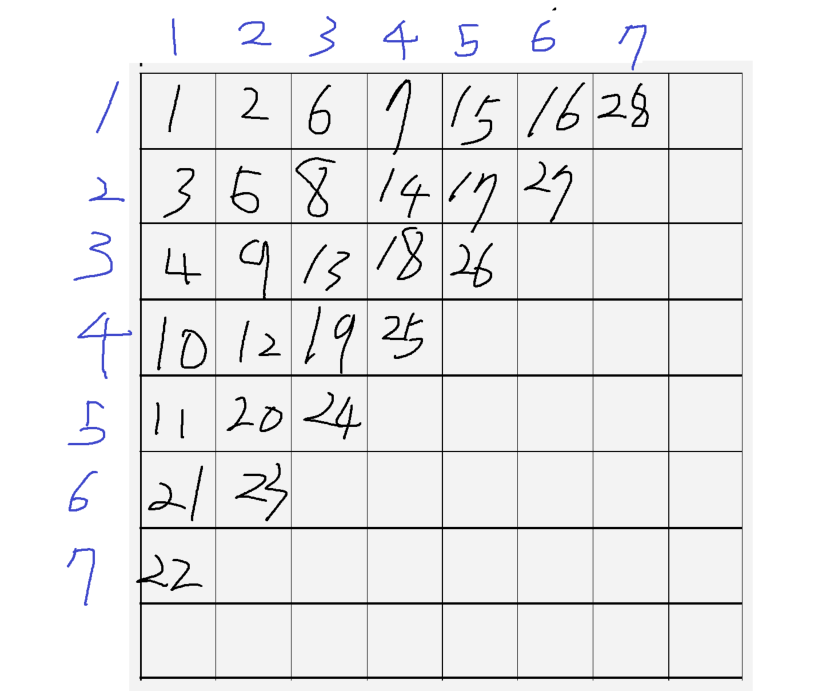
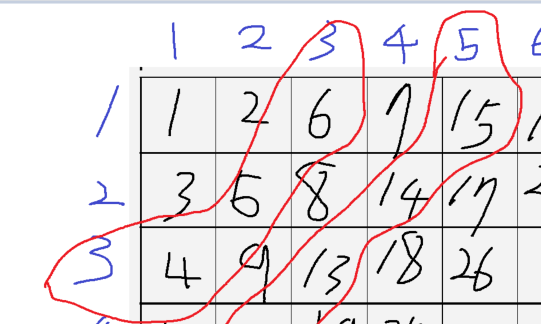
위 백준 문제를 표로 나타내면 이렇습니다.
뭔가 표가 어지럽지만,

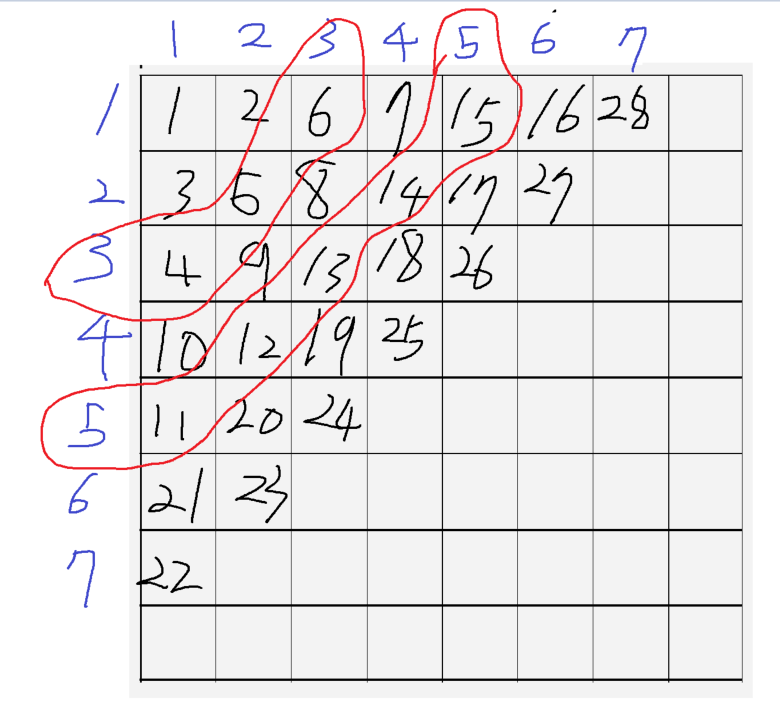
홀수 번째의 원소들만 반대로 출력된다면, 계차수열의 성질을 이용하여 풀 수 있을 것 같습니다.
그래서 돌렸습니다.

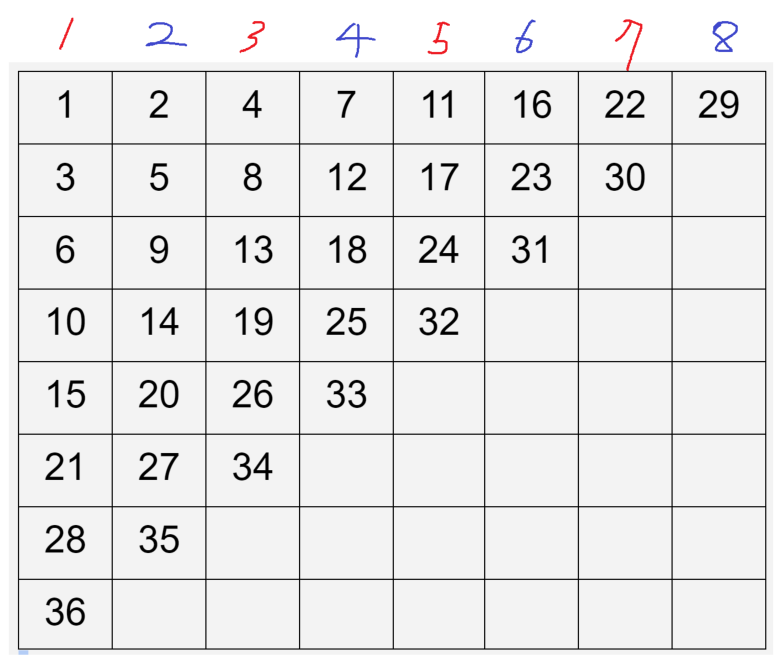
저는 '행'을 기준으로 풀었습니다.

1행을 잘 살펴보면, 고등학교 때 배웠던 계차수열이 생각 납니다.

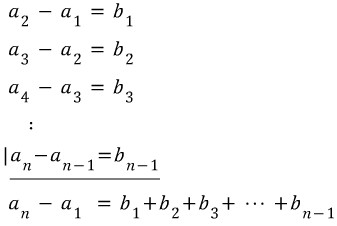
위 공식 대로 일반항을 구해보면
An = (1+2+3+...n-1) + 1입니다.
(1+2+3+...+n) = n(n-1) / 2

따라서, 1행의 일반항은 n(n-1) / 2 + 1입니다.

여기서, 구하고자 하는 X가 주어지면 이 일반항과 비교해야 합니다.
일반항에서 나오는 값은 1행의 값들이자 각 수 집합의 머리입니다.
족보로 따지면, 고조 할아버지입니다.

즉, (4, 5, 6)에서 족보 이름은 3, 고조 할아버지는 4입니다.

우리가 구해야 하는 것은 X가 속한 족보와 고조 할아버지입니다.
이를 위해서 일반항을 활용합니다.

먼저, 일반항에서 n의 값을 증가시키며 X와 비교합니다.
일반항에서 구한 값이 X보다 작다면, 계속해서 n을 증가시킵니다.
만약 일반항에서 구한 값이 X보다 커지는 순간이 온다면 바로 반복문을 탈출하고,
해당 족보 이름과 고조 할아버지를 확인합니다.

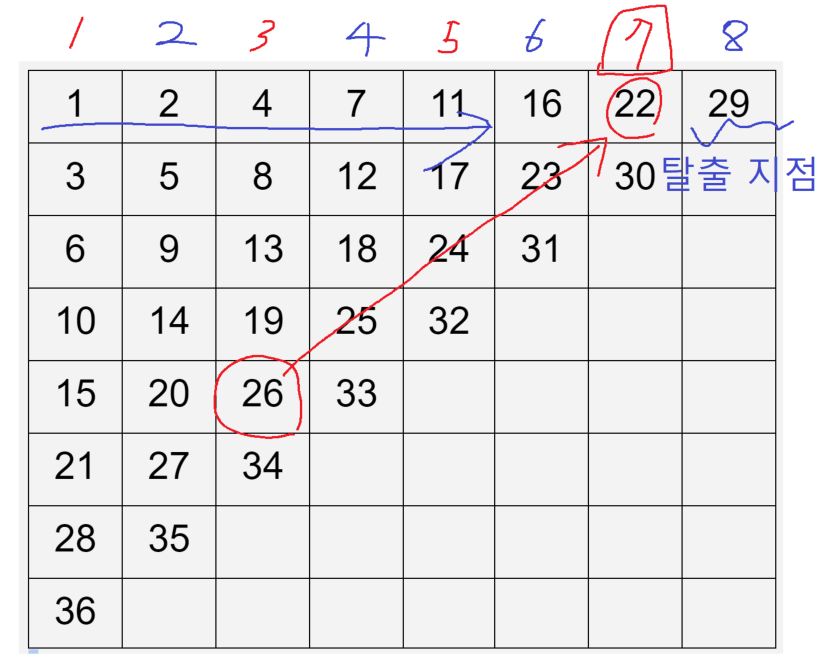
예시에서는 입력된 X = 26입니다.

위의 일반항 식에서 29가 탈출 지점이었을 테고, n값은 8이었습니다.
이 n의 값을 이용하여 26에 대한 족보 정보를 구합니다.
X의 족보 이름은 7이고 고조 할아버지는 22입니다.

이제 족보를 찾았으니, X에 대한 정보를 찾아들어가면 됩니다.
찾아 들어갈수록 '열'은 -, '행'은 +가 됩니다.
이렇게 족보를 찾아들어가면 최종 (5,3)의 값을 얻게 됩니다.

여기서 주의할 점) (5,3)은 정답이 아닙니다.

문제 풀이의 편의성을 위해 홀수 번째 족보는 모두 반대로 출력했습니다.
따라서, X가 홀수 번째 집안 사람이라면 행과 열을 바꿔서 답을 출력해야 합니다.

즉, 정답은 (3,5)입니다.

코드 참조)

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;

public class P1193 {

	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bfw = new BufferedWriter(new OutputStreamWriter(System.out));

		int X = Integer.parseInt(bfr.readLine());
		int n = 1;

		while (true) { // 찾으려는 수의 족보 뒤지기. 1~n번 족보까지 뒤져보기. 여기서 커지는 순간의 족보-1이 찾으려는 수의 족보.
			int tmp = (int) ((double) n * (n - 1) / 2 + 1);
			if (tmp > X)
				break;
			n++;
		}
		int greatGrandFather = (int) ((n - 1) * (n - 2) / (double) 2 + 1);
		int row = 1;
		int col = n - 1;
		while (true) {
			if (greatGrandFather == X) {
				if ((n-1) % 2 == 0)
					bfw.write(row + "/" + col);
				else
					bfw.write(col + "/" + row);
					break;
			}
			greatGrandFather++;
			row++;
			col--;
		}

		bfw.flush();
		bfw.close();
		bfr.close();
	}

}