
백준 2873번입니다. (전체 코드는 맨 아래에 있습니다.)
이 문제를 보자마자 '그냥 다 지나가면서 기쁨을 먹으면 되는 거 아닌가?' 하고 생각했습니다.
2x2 행렬부터, 행과 열을 1칸씩 늘려가며 계산해본 결과. 3가지의 경우를 찾을 수 있었습니다.
1) 행이 홀수일 때(즉, 행 값 % 2 != 0일 경우)
이 경우는 열의 경우를 생각하지 않아도 됩니다.
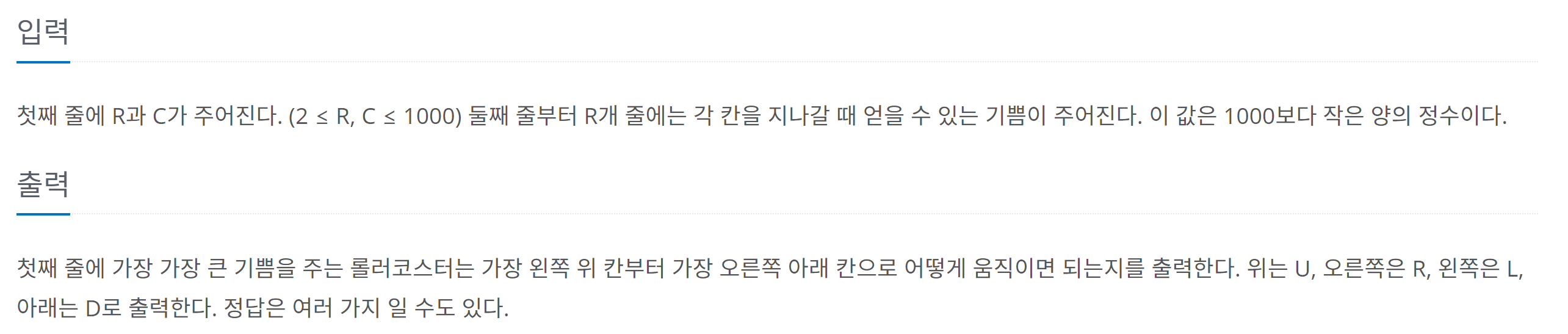
반드시 행렬의 모든 원소를 지나갈 수 있습니다. (ㄹ자로 그림 그리며 훑으면 됩니다.)
2) 열이 홀수일 때(즉, 열 값 % 2 != 0일 경우)

이 경우 또한 행의 경우를 생각하지 않아도 됩니다.
반드시 행렬의 모든 원소를 지나갈 수 있습니다. (이번엔 N자로 그림 그리며 훑으면 됩니다.)
3) 행과 열이 모두 짝수인 경우(즉, 행 % 2==0 && 열 % 2 ==0인 경우)
이 경우에 대해 생각하면서 정말 많은 시간을 소비하였습니다.
어떻게 그려도 절대 모든 원소를 훑을 수 없었습니다.
정말 많은 시도를 하여 2가지 경우로 나눌 수 있었습니다만, 해당 경우의 수가 최선의 값을
가져오는 것에 확신이 없어 다른 분의 풀이를 참고하였습니다.
참고 - [https://suhwanc.tistory.com/23]
감사하게도 다양한 그림과 자세한 설명으로 정말 좋은 참고가 되었습니다.
행렬의 모든 원소를 지나갈 수 없습니다. 최소한 1개의 원소는 버려지게 됩니다.
여기서 버릴 원소를 최소 1개, 혹은 그 이상을 선택해야 하는데 원소들의 합을 최대로 만들기 위해서는 단 1개만 버리는 게 가장 이상적입니다.
따라서, 3번 경우의 수는 버려질 1개의 원소를 고르는 게 목표입니다.
1개의 원소를 고르기 전에, 체스판 원리를 알고 가야 하지만 모르더라도 경험에 의해 알 수 있습니다.
3번의 경우는 짝수의 행,열이므로 최소값 2 x 2부터, 열을 2배씩 바꾸어가며 규칙을 찾아볼게요.
우선 2 x 2의 행렬을 살펴보겠습니다.

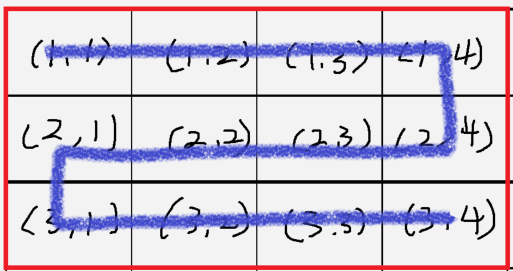
이 경우 (1,1)이 출발지, (2,2)가 도착지입니다.
(1,1)에서 (2,2)로 가기 위해서는 (2,1) 혹은 (1,2)를 버려야만 합니다.
(가장 작은 값을 가진 원소를 버려야 하지만, 여기서는 우선 규칙성을 찾는 것을 우선시하였습니다.)
(2,1)을 버렸을 경우
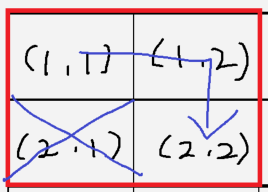
(1,2)를 버렸을 경우
아직까지는 규칙이 잘 보이지 않습니다.
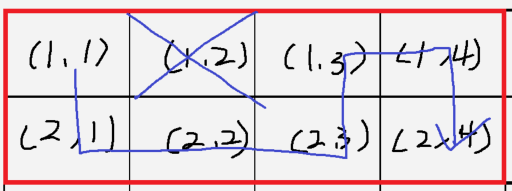
2 x 4의 행렬도 살펴보겠습니다.
(1,2)를 버렸을 경우
(1,3)을 버렸을 경우
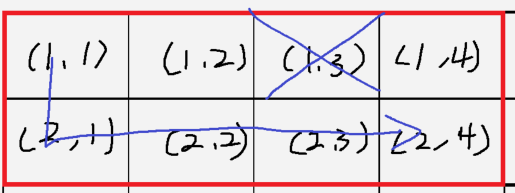
(1,3)을 버리니깐 2개의 손실이 발생합니다. 가장 이상적인 것은 1개만 버리는 건데,
이 경우는 안 될 것 같네요. 뭔가 규칙이 보이는 듯합니다.
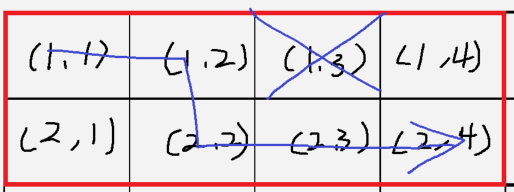
(1,4)를 버렸을 경우
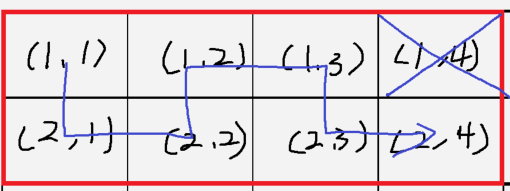
(2,1)을 버렸을 경우
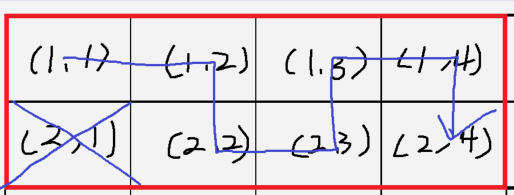
지금까지의 경우를 살펴보니, 원소의 좌표와 관련 있는 것 같습니다.
x(행), y(열)를 자세히 살펴보겠습니다.
x 좌표가 짝수면, y 좌표는 반드시 홀수.
x 좌표가 홀수면, y 좌표는 반드시 짝수여야지만 가장 이상적인 경우가 발생합니다.
규칙을 찾았으니, 이제 (짝, 홀), (홀, 짝)인 좌표 중 어떤 값을 버려야 할지 선택해야겠네요.
원소들의 합이 가장 커야 하니, 버려야 할 값은 가장 작은 값이면 되겠지요?
이제 특수한 경우도 모두 찾았으니, 조금 더 세부적인 논리를 짜야겠습니다.
세부 논리
1) 주어진 행이 홀수인가? - ㄹ 탐색
2) 주어진 열이 홀수인가? - N 탐색
3) 주어진 행과 열이 모두 짝수인가? - 특수 탐색
ㄹ 탐색과 N 탐색은 매우 쉽습니다.
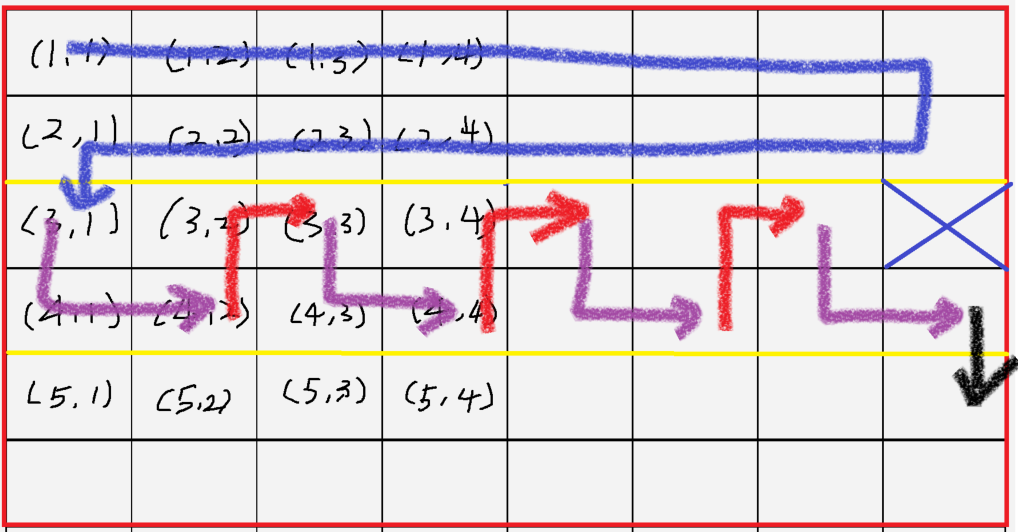
ㄹ 탐색 - 행열의 열을 따라 오른쪽 혹은 왼쪽으로 진행하다가, 경계선을 만나면 한 칸 아래로 내려간 후 반대 방향으로 쭉 진행. 이러한 과정을 마지막 행까지 반복하면 됩니다.
N 탐색 - 행열의 행을 따라 아래로 혹은 위로 진행하다가, 경계선을 만나면 한 칸 오른쪽으로 이동 후 아까와의 반대 방향으로 쭉 진행. 이러한 과정을 마지막 열까지 반복하면 됩니다.
코드 참조)
-ㄹ 탐색

trigger는 경계선에 부딪쳤을 경우, 진행 방향을 바꾸기 위해 사용됩니다.(왼 --> 오, 오--> 왼)
-N 탐색

여기서도 마찬가지로 trigger는 진행 방향을 바꿉니다. (아래 --> 위, 위 --> 아래)
특수 탐색은 입력으로 주어진 행과 열이 모두 짝수일 경우에만 사용됩니다.
우선, 버릴 원소 좌표를 구해야 합니다.
처음 입력받을 때 행과 열이 모두 짝수라면, (짝,홀) / (홀,짝)의 원소 값들을 모두 확인하며 최소값을 찾아야만 합니다.
코드 참조)
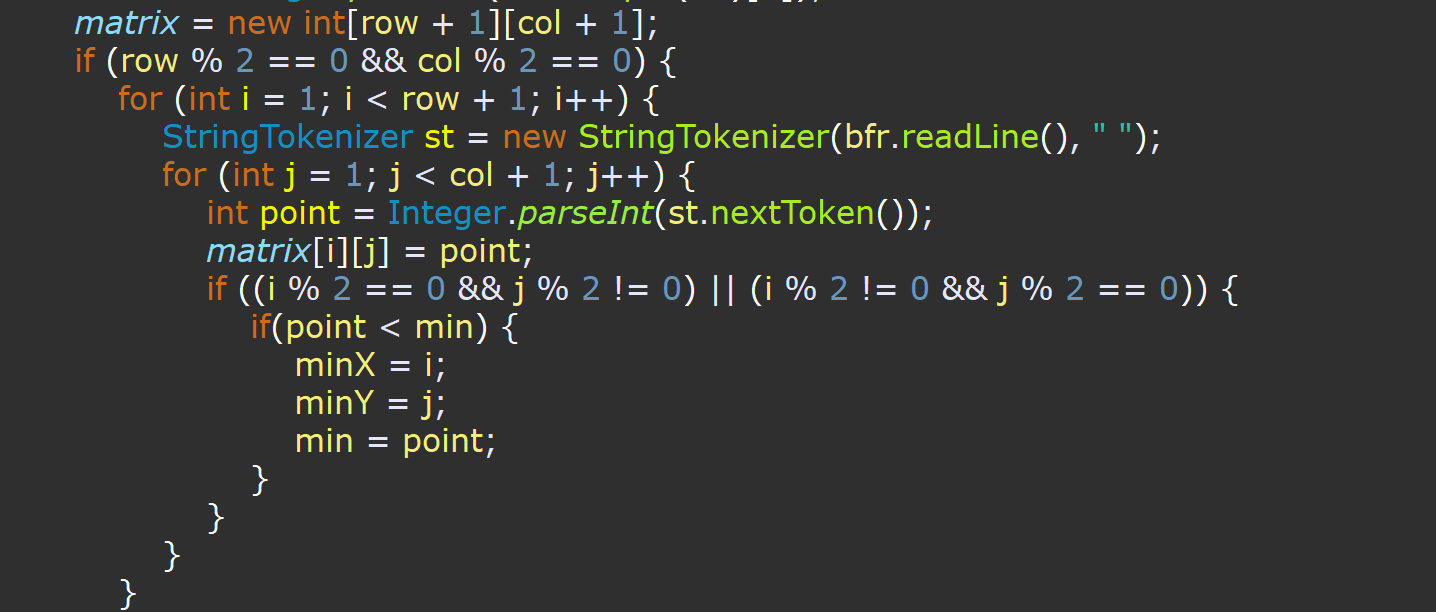
행렬의 시작을 (1,1)로 하기 위해서, 위처럼 행과 열에 +1을 하여 선언하였습니다.
입력받은 원소들을 행렬에 넣으면서, (짝,홀) / (홀,짝)의 원소는 행렬에 넣기 전에
최소값을 찾는 논리를 같이 실행합니다.
최종적으로 행렬에 모든 원소가 세팅되었을 때, minX와 minY는 (짝,홀) 혹은 (홀,짝)의 좌표를 가진 원소 중, 가장 작은 값을 가진 원소의 좌표를 가리키게 됩니다.
이제 버려야 할 원소의 좌표까지 알게 되었으니, 탐색을 진행해봅시다.
2 x 2 행렬의 경우
버려야 할 좌표가 (1,2)라면 경로는 단 하나입니다.
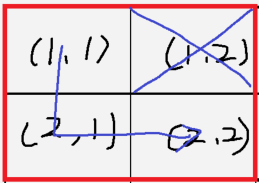
2 x 4 행렬의 경우
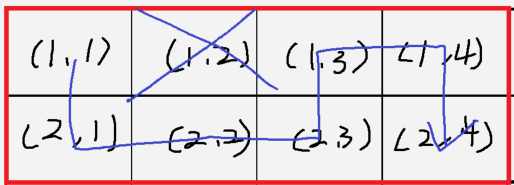
2 x 8 행렬의 경우
열이 커질수록, 모양이 뱀 같아서 뱀 탐색이라고 하겠습니다.
이러한 뱀 탐색을 사용한 이유는, 이 탐색을 사용해야 버리는 원소를 제외한 나머지 원소를 모두 탐색할 수 있기 때문입니다.



뭔가 규칙이 보이는 것 같네요.

규칙성을 더 찾으려면 행의 크기도 늘려야 할 것 같습니다.

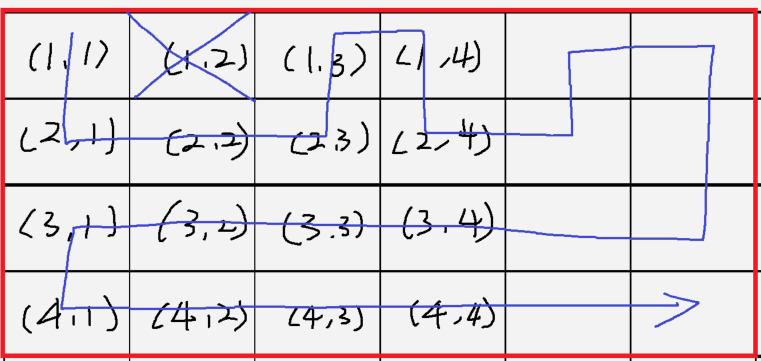
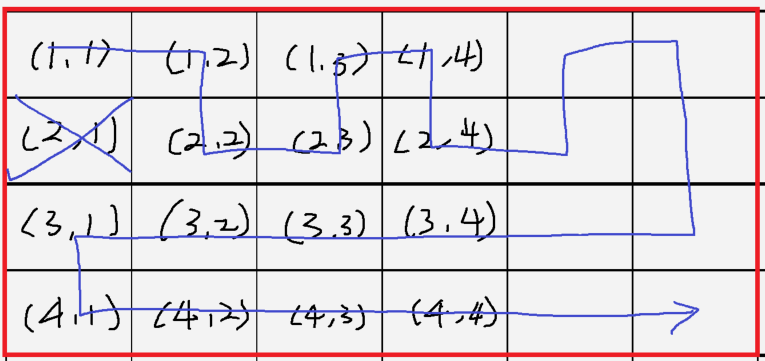

바로 위의 그림을 보니, 뭔가 보이는 것 같지 않나요? 다른 경우도 해보겠습니다.


이제 알 것 같습니다. 버려지는 원소의 행 영역에 진입하면, 기존에 진행하던 ㄹ 탐색에서 뱀 탐색으로 바꾸고, 특정 영역을 벗어나면 다시 ㄹ 탐색으로 쭉 진행하면 됩니다.
이제 특정 영역에 대해서 생각해보겠습니다.
1) 버려지는 원소의 행의 +1 혹은 -1에서는 뱀 탐색으로 진행하고, 해당 행에서 빠져나온 뒤
ㄹ 탐색으로 목적지까지 진행해야 합니다.
2) 뱀 탐색을 통해 버려지는 원소를 피해가는 경우는 2가지입니다.
2-1) 버려지는 원소의 행이 짝수일 경우, (버려지는 원소의 행 - 1)부터 뱀 탐색을 준비해야 합니다. 그리고 (버려지는 원소의 행 + 1)부터 ㄹ 탐색으로 목적지까지 가면 됩니다.
2-2) 버려지는 원소의 행이 홀수일 경우, (버려지는 원소의 행)부터 뱀 탐색을 준비해야 하며, (버려지는 원소의 행 +2)부터 ㄹ 탐색으로 목적지까지 가면 됩니다.
2-3) 만약 출발 지점이 버려지는 2-1), 2-2)의 상황이라면 그 즉시 뱀 탐색으로 시작합니다.
위의 가설을 토대로 논리 구조를 세우겠습니다.
탐색 시작
A) 버려지는 원소의 행이 짝수인가, 홀수인가?
B) 버려지는 원소의 행과 출발 지점과의 거리 확인
C) 버려지는 행까지 ㄹ 탐색, 특정 영역 진입 후 뱀 탐색. 해당 영역 벗어나면 다시 ㄹ 탐색
혹은 목적지 도착 확인했으면 탐색 종료.
뱀 탐색은 짝수 / 홀수에 따라 2가지의 형태, 그리고 세부적으로 2가지 총 4가지의 형태가 나타납니다.
먼저 짝수의 경우,
위처럼 (짝수, 전체 열 -3,-5...)의 형태, 그리고 또다른 (짝수, 전체 열 -1)의 형태입니다.
(짝수, 전체 열 -3~)의 형태는 항상 마지막에 (버려지는 원소의 행-1, 전체 열)에 도달합니다.
경계선을 확인하고, ㄹ 탐색을 위해 2칸 아래로 내려가야 합니다.
그리고 버려지는 원소가 항상 바로 아래에 나타납니다. (아래 그림 참조)

참고) 짝수의 경우 움직임이 3가지가 있습니다.
버려지는 원소를 만나기 전까지 Down + Right(DR, 보라색) / Up + Right(UR, 빨간색)
만난 후 Right(R, 회색)
(짝수, 전체 열-1)의 형태는
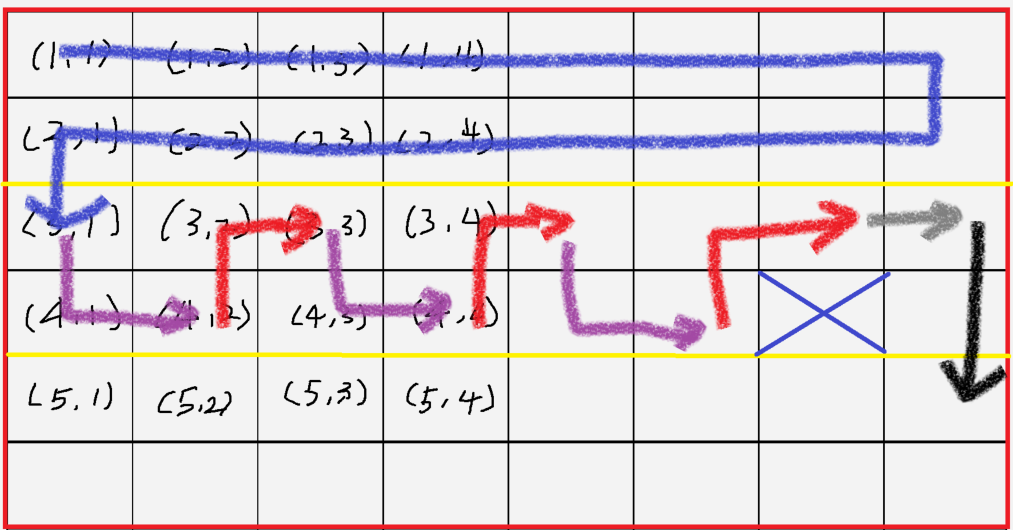
위 그림을 보면, 2칸을 한 번에 내려갔는데, 코드 상에서는 공통 1칸, 그리고 개별적 1칸으로 구현했습니다. (버려지는 원소의 행이 홀수인 경우와 공통 코드)
홀수의 경우도 마찬가지입니다.
홀수의 경우는 회색 화살표(회피 기동) 부분만 다릅니다.
그러나, 경계 영역이 다르므로 코드를 따로 구현해줘야 합니다.
홀수의 경우 경계 영역(노란 선) = 해당 행 ~ 행+1
짝수의 경우 경계 영역(노란 선) = 해당 행-1 ~ 해당 행
그리고 짝수/홀수 모두 주의해야 할 것이 있습니다.
각각 2가지씩 총 4가지의 경우에 대해 경계 영역(노란 선)을 나갈 수 있도록 조건을 총 4개를 걸어주는 것과, 출발 지점과 버려지는 행의 위치 관계 등을 고려해야 합니다.
그리고 버려지는 원소에 대한 뱀 탐색이 끝난 후, 다시 ㄹ 탐색을 진행할 때 반드시 trigger를 반대로 설정해줘야 정상적인 진행 방향을 잡습니다.
뱀 탐색 시작 전, trigger를 건드려 왼쪽 --> 오른쪽으로 방향을 바꿨기 때문입니다.
다시 ㄹ자 탐색을 통해 오른쪽 --> 왼쪽으로 가야 하므로 설정을 바꿔줘야 합니다.
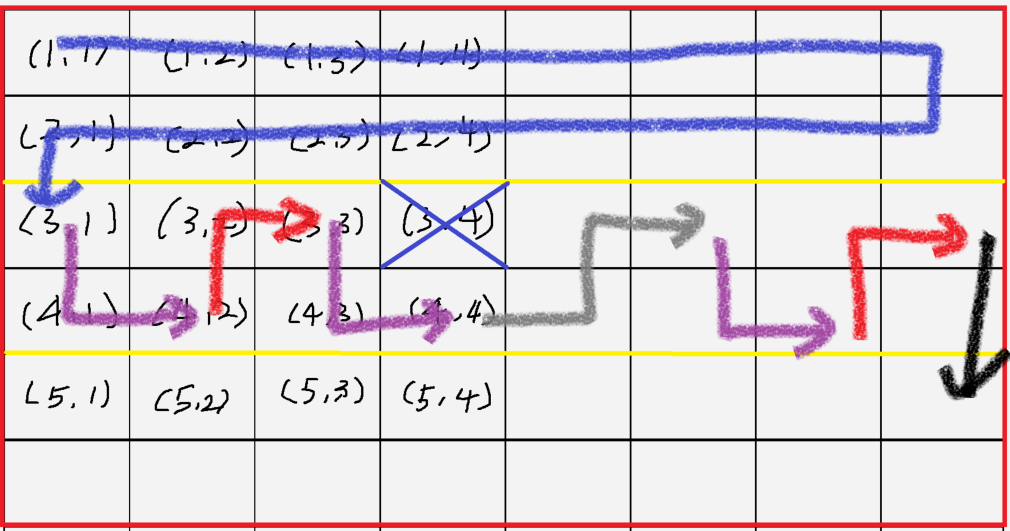
코드 참조)
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
static int[][] matrix;
public static void main(String[] args) throws IOException {
BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bfw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
String mInfo = bfr.readLine();
int min = Integer.MAX_VALUE;
int minX = 0;
int minY = 0;
int row = Integer.parseInt(mInfo.split(" ")[0]);
int col = Integer.parseInt(mInfo.split(" ")[1]);
matrix = new int[row + 1][col + 1];
if (row % 2 == 0 && col % 2 == 0) {
for (int i = 1; i < row + 1; i++) {
StringTokenizer st = new StringTokenizer(bfr.readLine(), " ");
for (int j = 1; j < col + 1; j++) {
int point = Integer.parseInt(st.nextToken());
matrix[i][j] = point;
if ((i % 2 == 0 && j % 2 != 0) || (i % 2 != 0 && j % 2 == 0)) {
if (point < min) {
minX = i;
minY = j;
min = point;
}
}
}
}
} else {
for (int i = 1; i < row + 1; i++) {
StringTokenizer st = new StringTokenizer(bfr.readLine(), " ");
for (int j = 1; j < col + 1; j++) {
int point = Integer.parseInt(st.nextToken());
matrix[i][j] = point;
}
}
}
if (row % 2 != 0) {
boolean trigger = true;
int i = 1;
while (true) {
if (!trigger) {
for (int j = col; j > 1; j--)
sb.append("L");
trigger = true;
} else {
for (int j = 1; j < col; j++)
sb.append("R");
trigger = false;
}
if (i < row) {
sb.append("D");
i++;
} else
break;
}
} else if (col % 2 != 0) {
boolean trigger = true;
int j = 1;
while (true) {
if (trigger) {
for (int i = 1; i < row; i++)
sb.append("D");
trigger = false;
} else {
for (int i = row; i > 1; i--)
sb.append("U");
trigger = true;
}
if (j < col) {
sb.append("R");
j++;
} else
break;
}
} else {
int blockRow = minX;
int blockCol = minY;
// 시작
int i = 1;
int j = 1;
boolean trigger = false; // ㄹ자 탐색을 위함.
while (true) {
if (blockRow % 2 != 0) { // blowRow가 홀수일 경우.
if (i == blockRow) {
while (true) {
sb.append("DR");
i++;
j++;
if (i - 1 == blockRow && j == blockCol) { // DR사이클에서 끝날 경우와
if (blockRow != row && blockCol != col) {// UR 사이클에서 끝날 경우
sb.append("RUR");
i--;
j += 2;
} else // block처리한 곳이 사각형의 꼭지점일 때. 즉 DR 사이클에서 끝남.
break;
} else {
sb.append("UR");
i--;
j++;
}
if (j >= col) {// block이 꼭지점에 위치한 경우가 아니면, 항상 UR에서 끝난다.
sb.append("D");
i++;
break;
}
}
if (i < row) { // 마지막 행이 아니라면, 다시 ㄹ 탐색을 위해서 아래로 내려줘야 한다.
sb.append("D"); // 다시 정상 궤도 진입시키기.
trigger = true; // 왼쪽으로 진행시켜야 함. blockRow가 홀수일 때는 항상 오른쪽을 가리키다가 blockRow에 들어가기 때문에,
// trigger를 뒤집어줄 필요가 있다.
i++;
}
// 여기까지 홀수에 대한 뱀 탐색
}
} else { // blockRow가 짝수인 경우.
if (i == blockRow - 1) { // R에서 끝나는 경우와 UR에서 끝나는 경우가 있다.
while (true) {// R에서 끝나는 경우는, 맨뒤에서 두 번째가 block일 경우.
if (i + 1 == blockRow && j == blockCol) {
sb.append("R");
j++;
if (j < col) {
sb.append("DR");
i++;
j++;
}
} else {
if (j < col) {
sb.append("DR");
i++;
j++;
}
}
if (j < col) {
sb.append("UR");
i--;
j++;
} else {
sb.append("D");
i++;
break;
}
}
if (i < row) { // 마지막 행이 아니라면, 다시 ㄹ자 탐색을 위해서 아래로 내려줘야 한다.
sb.append("D"); // 다시 정상 궤도 진입시키기.
trigger = true; // 왼쪽으로 진행시켜야 함. blockRow가 홀수일 때는 항상 오른쪽을 가리키다가 blockRow에 들어가기 때문에,
// trigger를 뒤집어줄 필요가 있다.
i++;
}
}
// 여기까지 짝수에 대한 뱀 탐색
}
// blockRow에 대한 뱀 탐색 후, 정상 ㄹ자 탐색.
if (trigger) {
for (; j > 1; j--)
sb.append("L");
trigger = false;
} else {
for (; j < col; j++)
sb.append("R");
trigger = true;
}
if (i < row) {
sb.append("D");
i++;
} else
break;
}
}
bfw.write(sb.toString() + "\n");
bfw.flush();
bfw.close();
bfr.close();
}
}
예시 입력)
2 2
2 255
1 2
2 2
2 1
255 2
4 4
2 2 2 2
2 2 2 2
2 2 2 1
2 2 2 2
2 4
2 2 2 2 2 2 2 1
2 2 2 2 2 2 2 2
2 6
2 2 2 2 1 1
2 2 2 2 2 2
2 6
2 2 2 2 2 2
2 2 2 2 1 2
4 6
2 2 2 2 2 2
1 2 2 2 2 2
2 2 2 2 2 2
1 2 2 2 2 2
4 6
2 2 2 2 1 1
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
4 4
2 2 2 2
2 2 1 2
2 2 2 2
2 2 2 2
4 4
2 1 2 2
2 2 2 2
2 2 2 2
2 2 2 2
4 4
2 2 2 1
2 2 2 2
2 2 2 2
2 2 2 2
4 4
2 2 2 2
1 2 2 2
2 2 2 2
2 2 2 2
4 4
2 2 2 2
2 2 2 2
2 2 2 2
2 2 1 2
4 4
2 2 2 2
2 2 2 2
2 2 2 1
2 2 2 2
6 6
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 1 2
6 6
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2 2 2 1
2 2 2 2 2 2
