Tree

개념

• 계층적 관계를 표현하는 자료구조로 비선형 자료구조이다.
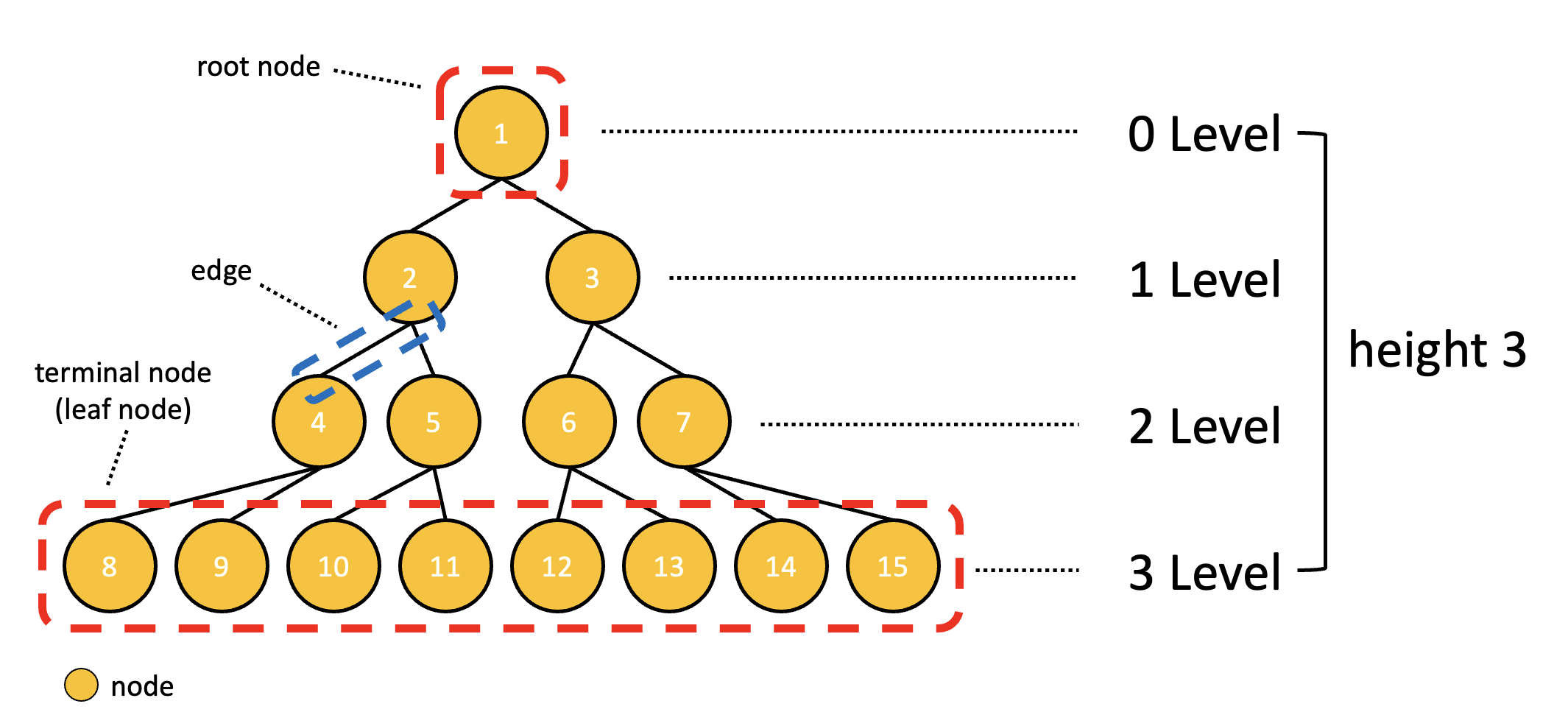
• 노드(node)와 엣지(edge)로 구성되어 있다.
• 노드는 가장 최상위 노드인 root node, 자식 노드를 가지고 있지 않은 terminal node(leaf node), 1개 이상의 자식 노드를 가지고 있는 internal node로 나눌 수 있다.
• 층(level)이라는 개념이 있으며 root node를 0 level이라고 한다.
• 트리에서 나올 수 있는 최대 level를 그 트리의 높이(height)라고 한다.
  

종류

Binary Tree (이진 트리)

• root node를 중심으로 두 개의 서브 트리로 나뉜다.
• 나뉘어진 두 서브 트리 또한 이진 트리를 만족한다.
• 공집합도 이진 트리에 포함된다.
• 노드가 하나인 트리도 이진 트리에 포함된다.
• 배열로 두성된 이진 트리는 노드의 개수가 n이고 root node의 시작이 0이 아닌 1일 때, i번째 노드에 대해서 부모 노드는 i/2, 자식 노드는 2i, 2i+1의 인덱스를 가진다.

Complete Binary Tree (완전 이진 트리)

• 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 차곡차곡 채워진 이진 트리

Full Binary Tree (정 이진 트리)

• 모든 노드가 0개 또는 2개의 자식 노드를 갖는 이진 트리

Perfect Binary Tree (포화 이진 트리)

• 모든 level에 노드가 꽉 찬 이진 트리

Binary Search Tree (이진 탐색 트리, BST)

• 이진 트리의 일종으로 데이터를 저장하는 규칙이 있고, 그 규칙은 특정 데이터의 위치를 찾는데 이용된다.
  • BST의 노드에 저장된 키는 유일하다.
  • 부모의 키가 왼쪽 자식 노드의 키보다 크다.
  • 부모의 키가 오른쪽 자식 노드의 키보다 작다.
  • 왼쪽과 오른쪽의 서브 트리도 BST이다.
• BST에서 탐색(search) 연산의 시간 복잡도는 O(log n)이다. (엄밀히 말하면 O(height))
• 저장 순서에 따라 한 쪽으로만 노드가 추가되는 경우 Skewed Tree(편향 트리)가 될 수 있다. 이 경우 탐색(search)의 Worst Case가 되고, 시간 복잡도는 O(n)이 된다.
• 편향 트리의 균형을 잡기 위한 트리 구조의 재조정을 Rebalancing이라고 하며 여러 Rebalancing 기법을 적용한 트리 중 하나가 Red-Black Tree이다.

Binary Heap

• 최대값 및 최소값을 찾아내는 연산을 빠르게 하기 위해 고안된 자료구조로 우선순위 큐(Priority Queue)를 구현하는 방법 중 하나이다.
• 자료구조의 일종으로 Tree의 형식을 하고 있고, Tree 중에서도 배열에 기반한 완전 이진 트리의 일종이다.
• 사용할 때 0번은 편의를 위해 비워두고 1번 인덱스부터 사용한다.
• 최대 힙(Max Heap)과 최소 힙(Min Heap)이 있다.
• Max Heap은 각 노드의 값이 자식 노드들보다 크거나 같아야 되는 조건을 만족해야 되며, Min Heap은 그 반대이다. (완전 이진 트리는 값의 중복이 허용되지 않지만, Heap은 허용된다.)
• Max Heap에서 최대값을 찾는데 시간 복잡도는 O(1)이다. 마찬가지로 Min Heap에서 최소값을 찾는데 시간 복잡도도 O(1)이다.
• 삽입과 삭제 작업을 진행하는 경우 작업 후 Heapify를 통해 계속해서 Heap 구조를 유지해야 되기 때문에 걸리는 시간 복잡도는 O(log n)이다.