Graph
- 정점(Vertex)과 간선(Edge)의 집합
- 트리 또한 사이클이 허용되지 않은 그래프
- 간선의 방향 여부에 따라 방향 그래프와 무방향 그래프로 나뉜다.
- Degree: 무방향 그래프에서 한 정점에 연결된 간선의 수로 방향 그래프에서는 방향이 있기에 정점에서 나가는 OutDegree와 정점으로 들어오는 InDegree로 나뉜다.
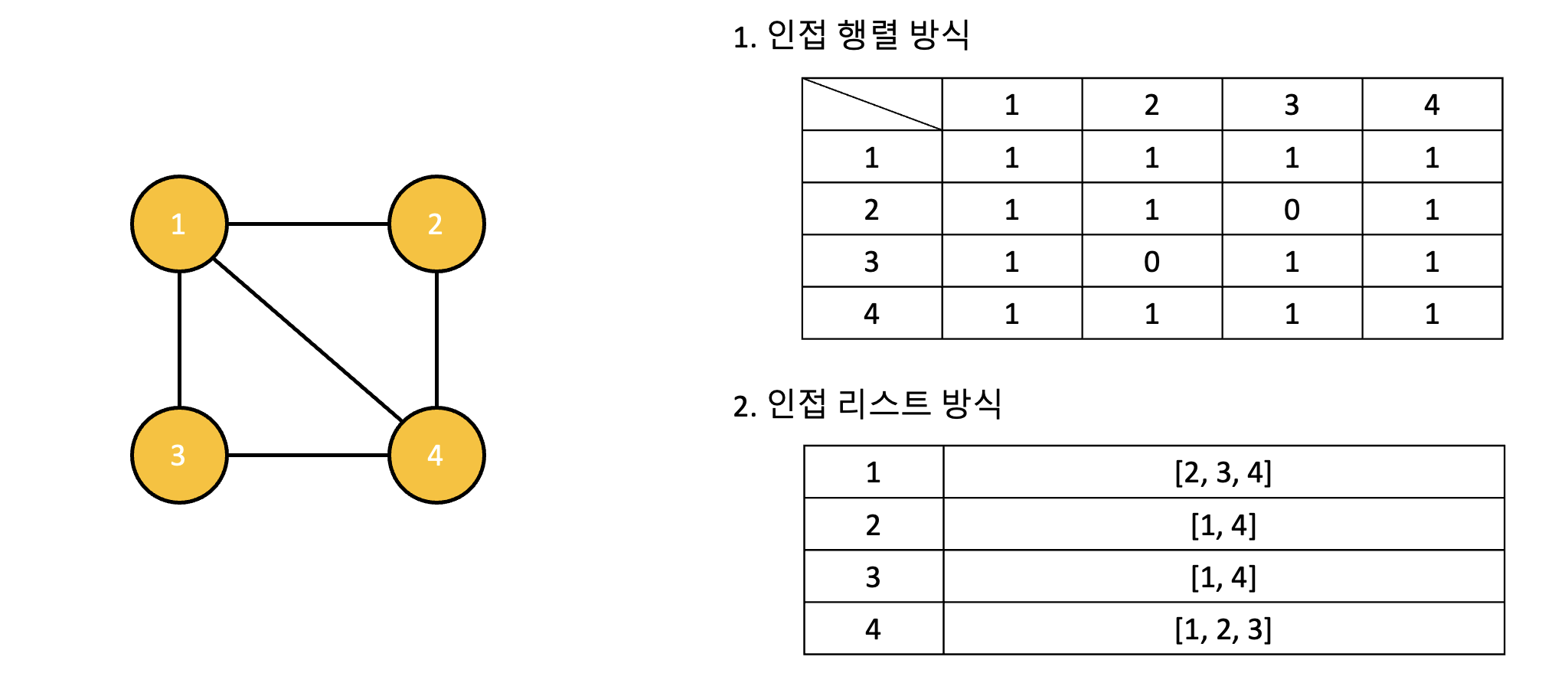
구현 방법
- 인접 행렬
- 정방행렬을 사용한다.
- 정점과의 연결관계를 확인하는 시간 복잡도는
O(1)이다.
- 구현에 필요한 공간 복잡도는
O(V^2)이다.
- 밀집 그래프를 나타내기에 적합하다.
- 인접 리스트
- 연결리스트를 사용한다.
- 구현에 필요한 공간 복잡도는
O(V+E)이다.
- 희소 그래프를 나타내기에 적합하다.
탐색
- DFS (Depth First Search)
- Stack을 사용해서 구현
O(V+E)의 시간 복잡도
- BFS (Breadth First Search)
- Queue을 사용해서 구현
- 탐색을 시작할 정점을 Inqueue하고 시작하며, 해당 정점을 dequeue하면서 연결된 모든 정점을 Inqueue하는 것을 반복한다.
O(V+E)의 시간 복잡도- 간선의 가중치가 없거나 모든 간선의 가중치가 동일하다면 BFS로 구한 경로는 최단 경로이다.
스패닝 트리 (Spanning Tree)
- 그래프 G의 모든 정점이 사이클없이 연결된 형태
- 정점이 N개일 때 간선은 N-1개이다.
최소 스패닝 트리 (MST - Minimum Spanning Tree)
- 그래프 G에서 나올 수 있는 스패닝 트리 중, 간선의 가중치 합이 최소인 스패닝 트리
- 구하는 대표적인 알고리즘으로 크루스칼 알고리즘, 프림 알고리즘이 있다.

